Krigage
The krigeage, kriging or kriging (from the French krigeage), also known as regression in Gaussian processes, it is a geostatistical interpolation method of point estimation. It uses a variogram model to obtain the weights that are given to each reference point used in the estimation. This interpolation technique is based on the premise that the spatial variation continues with the same homogeneous pattern. It was initially developed by Danie G. Krige from the regression analysis between samples and ore blocks, which established the basis of linear geostatistics.
Introduction
Kriging can be understood as linear prediction or a form of Bayesian inference. Part of the principle: near points in space tend to have values more similar than the most distant points. The kriging technique assumes that the data collected from a certain population is correlated in space. That is, if in a toxic and dangerous waste dump the zinc concentration at a point p is x, it will be very likely that results will be very close to x the closer one is to point p (principle of geostatistics). However, from a certain distance from p, values close to x will certainly not be found because the spatial correlation may cease to exist.
The kriging method is considered to be of the type MELI (Best Linear Unbiased Estimator) or ELIO (Optimal Linear Unbiased Estimator): it is linear because their estimates are weighted linear combinations of existing data; and it is unbiased because it ensures that the mean of the errors (deviations between the real value and the estimated value) is zero; is the best (optimal) because the estimation errors have a minimum variance (estimate variance). The term kriging encompasses a number of methods, the most common being the following:
Types of Kriging
Simple Kriging
Assumes that local means are relatively constant and of value very close to the known population mean. The population mean is used for each local estimate, in conjunction with the neighboring points established as necessary for the estimate.
Ordinary Kriging
Local means are not necessarily close to the population mean, only neighboring points are used for estimation. It is the most widely used method in environmental problems.
Cooking
It is an extension of the above situations in which two or more variables have a spatial dependence and that variable is estimated to not show up as strongly as others are dependent variables, using these values and their dependencies to estimate the variable that is required.
Mathematical concepts
The Kriging method uses various theories developed in statistics. Meanwhile, for this statistical theory to be seen more clearly in the field of application; Some concepts are explained.
Semivariance and semivariogram
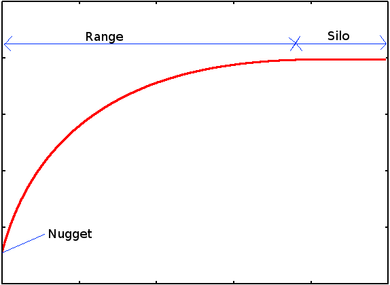
A semivariance is a measure of the degree of spatial dependence between two samples. The magnitude of the semivariance between two points depends on the distance between them, implying smaller semivariances for smaller distances and larger semivariances for larger distances. The graph of the semivariances as a function of the distance to a point is called a semivariogram. After a certain distance, the semivariance will no longer increase with distance and will stabilize at a value equal to the mean variance, giving that region the name plateau, silo or patamar (sill)[citation required]. The distance between the beginning of the semivariogram and the beginning of the silo is called the range. By extrapolating the semivariogram curve for zero distance, we can arrive at a nonzero value of semivariance. This value is called the nugget effect (Nugget Effect).
Variogram Models
In the Kriging Method four types of variograms are normally used: the following variables are used:
- v{displaystyle v,}: variance
- c0{displaystyle c_{0},}: nugget
- a{displaystyle a,}: silo
- c0+c{displaystyle c_{0}+c,}: asymptotic variance
- h{displaystyle h,}: separation distance
Linear
This model has no chair and is very simple. Its curve can be represented by:
- v=c0+ch{displaystyle v=c_{0}+ch,}
Spherical
A spherical shape is the most commonly used in the silo. Its shape is defined by:
- <math alttext="{displaystyle v={begin{cases}c_{0}+c[1.5({frac {h}{a}})-0.5({frac {h}{a}})^{3}],&{mbox{se }}haend{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">v={c0+c[chuckles]1.5(ha)− − 0.5(ha)3],♪h.ac0+c,♪h▪a{displaystyle v={begin{cases}c_{0}+c[1.5({frac {h}{a}}{a})-0.5({frac {h}{a}}}}}})^{3},{{{{mbox{se }}}}}}{c_{c_{0} +c,{mbox{mbox{se }}}}}}}}}{<img alt="{displaystyle v={begin{cases}c_{0}+c[1.5({frac {h}{a}})-0.5({frac {h}{a}})^{3}],&{mbox{se }}haend{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/53fb4dab4f203f32de95dbb21c66ccf8f9c3e4f7" style="vertical-align: -2.505ex; width:42.111ex; height:6.176ex;"/>
Exponential
The exponential variogram curve respects the following equation:
- v=c0+c(1− − e− − hb){displaystyle v=c_{0}+c(1-e^{frac {-h}{b}}}}},
Gaussian
A Gaussian form is given by:
- <math alttext="{displaystyle v={begin{cases}c_{0}+c(1-e^{frac {-h^{2}}{a^{2}}}),&{mbox{se }}haend{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">v={c0+c(1− − e− − h2a2),♪h.ac0+c,♪h▪a{displaystyle v={begin{cases}c_{0}+c(1-e^{frac {-h^{2}}}{a^{2}}}}}}}),{{mbox{se }}}}}}{c({c_{0},{mbox{se }}h purviti}}}<img alt="{displaystyle v={begin{cases}c_{0}+c(1-e^{frac {-h^{2}}{a^{2}}}),&{mbox{se }}haend{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d20b5e329d813358945360821f0818bfeea142ae" style="vertical-align: -3.338ex; width:34.496ex; height:7.843ex;"/>
Kriging method
Determination of the semivariogram
Based on a simulation of a two-dimensional (2D) system containing a finite number of points where a measurement of any size is possible. After the acquisition of these data, the Kriging interpolation will begin seeking to achieve a higher resolution. The first step is to construct an experimental semivariogram. For this, the semivariance of each point in relation to the others is calculated and seen in a graph of the semivariance by the distance.
- v(h=dip)=12n␡ ␡ i=1n(fi− − fp)2{displaystyle v(h=d_{ip})={frac {1}{2n}}sum _{i=1^{n}(f_{i}-f_{p})^{2}}}}
From this graph, the variogram model that best approximates the curve obtained is estimated. The nugget effect may be present in the experimental semivariogram and must be considered. Once the semivariogram model to be used has been determined, the calculation phase begins. Since the semivariogram is a function that depends on the direction, it is natural that it presents different values according to the direction, receiving this phenomenon the name of anisotropy. A case of semivariogram presenting a similar shape in all directions of space will depend on h, saying that it is an isotropic structure, i. e., without privileged directions of variability.
Calculation of Weights
Consider, for the calculation of the kriging, the following formula:
- F(x,and)=␡ ␡ i=1nwifi{displaystyle F(x,y)=sum _{i=1}^{n}w_{if}{i}}
where n{displaystyle n} is the number of samples obtained, fi{displaystyle f_{i} is the value obtained at the point i{displaystyle i} and wi{displaystyle w_{i}} is the weight designated to the point i{displaystyle i}. In order to get the weights of each of the n{displaystyle n} points, for each of them a calculation of w1,w2,...,wn{displaystyle w_{1},w_{2},. Such proceeding depends on the type of kriging that is being used. We emphasize the following notation:
- wj{displaystyle w_{j},}: weight j-ésimo point
- S(dij){displaystyle S(d_{ij}),}: value of the semivariance dij{displaystyle d_{ij}}
- λ λ {displaystyle lambda ,}: temporary variable
Ordinary Kriging
In this case the local mean of the displayed points is used. Therefore, the mean of the weights should be normalized. Consequently, there is a more accurate result of Simple Kriging. The following equations will be used to determine the values of the weights at the p-th point:
- {w1S(d11)+w2S(d12)+...+wnS(d1n)+λ λ =S(d1p)w1S(d21)+w2S(d22)+...+wnS(d2n)+λ λ =S(d2p) wnS(dn1)+w2S(dn2)+...+wnS(dnn)+λ λ =S(dnp)w1+w2+...+wn=1## ############################################################################################################################################################
Simple Kriging
For this case, use the average of all data. By imposing, therefore, that it is not normalized in the average location of the pesos, as in the previous one. Thus, we have almost the same equation, except for the exclusion of λ λ {displaystyle lambda } and the last equation. The main feature of this method is the generation of smoother and more aesthetically soft graphics. It should be noted that this case is less accurate than the previous case. Weight values for the p-simo point will be given by:
- {w1S(d11)+w2S(d12)+...+wnS(d1n)=S(d1p)w1S(d21)+w2S(d22)+...+wnS(d2n)=S(d2p) wnS(dn1)+w2S(dn2)+...+wnS(dnn)=S(dnp)♪♪
Obtain Interpolated Point
When we get to the values of w1,w2,...,wn{displaystyle w_{1},w_{2},, the values are calculated fp{displaystyle f_{p}}:
- fp=w1f1+w2f2+...+wnfn{displaystyle f_{p}=w_{1}f_{1}+w_{2}f_{2}+w_{n}f_{n},}
That way, the interpolated value is calculated for all desired points. It is emphasized that only the values acquired above should be used.
Interpolating Other Points
Obtaining the interpolated value at another point requires repeating all the calculations performed from obtaining the variogram model. In this way, to increase the resolution that was intended, mathematical methods must be used for computational resolution. Various codes have been developed for that resolution, but one of the best algorithms can be obtained from the link below. It was initially made for the Fortran language, and can be recoded for C with the help of the fortran2c library, presenting itself entirely in C:
Contenido relacionado
Lapiaz
Zero divisor
Closed and exact differential forms