Koch Snowflake

ImprimirCitar

Artistic conception of a Koch Copo. We call Koch's copy to the curve describing the figure outline.

The Koch snowflake, also called Koch's star or Koch's island, is a continuous but non-differentiable closed curve at no point described by the Swedish mathematician Helge von Koch in 1904 in an article entitled "On a continuous curve possessing no tangents and obtained by the methods of elementary geometry".

In current language, we would say that it is a fractal curve. Its simplest construction is carried out through an iterative process that begins by dividing a line segment into three and inserting two more in the middle third in the form of an equilateral triangle, the process is repeated an infinite number of times. The Koch curve is a particular case of the De Rham curve.

Construction

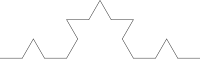
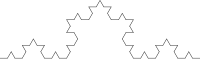
Let's see the process that leads to replacing each side by the so-called Koch curve: Take a segment, divide it into three equal parts, replace the central part by two parts of equal length making an angle of 60 degrees. Then, with all four segments, we proceed in the same way, resulting in 16 smaller segments in the second iteration. And so on. The figure represents the first six stages of construction. The last curve is a good approximation of the final curve.

**Koch curve construction**
1.a iteration	2.a iteration	3.a iteration

4.a iteration	5.a iteration	6.a iteration

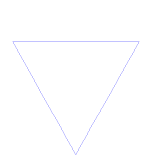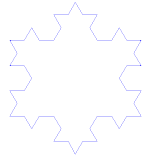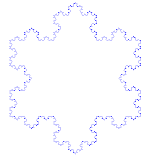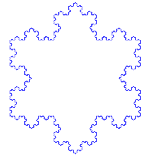
Three of these curves joined together form the Koch snowflake and the Koch anti-snowflake:

Koch snowflake (6 iterations)

Koch snowflake (5 iterations)

Representation as a Lindenmayer system

The Koch curve can be expressed in the Lindenmayer system

 Alphabet: F
Constant: +, −
Axioma: F++F++F
Production rules:
F → F−F++F−F

Here, F means "continue drawing", + "turn 60 degrees to the right, and -" turn 60 degrees to the left" (see turtle graphs)

Properties

Perimeter of the Koch Snowflake

Each iteration multiplies the number of sides in the Koch snowflake by four, so the number of sides after the iterations $n$ is given by:

{displaystyle N_{n}=N_{n-1}cdot 4=3cdot 4^{n},.}

If the original equilateral triangle has sides of length $s$ , the length of each side of the snowflake after iterations $n$ is:

{displaystyle S_{n}={frac {S_{n-1}}{3}}={frac {s}{3^{n}}},,}

an inverse power of three multiple of the original length. The perimeter of the snowflake after $n$ iterations is:

{displaystyle P_{n}=N_{n}cdot S_{n}=3cdot scdot {left({frac {4}{3}}right)}^{n},.}

The Koch curve has infinite length, because the total length of the curve increases by a factor of 4/3 with each iteration. Each iteration creates four times as many line segments as the previous iteration, the length of each being 1 /3 the length of the segments in the previous stage. Therefore, the length of the curve after $n$ iterations will be (4/3) ^$n$ times the perimeter of the original triangle and is unbounded, since $n$ tends to infinity.

Perimeter Boundary

As the number of iterations tends to infinity, the limit of the perimeter is:

{displaystyle lim _{nrightarrow infty }P_{n}=lim _{nrightarrow infty }3cdot scdot left({frac {4}{3}}right)^{n}=infty ,,}

where |4/3| > 1.

There is a dimensional measure ln 4/ln 3, but so far it has not been calculated. Only the upper and lower limits have been invented.

Koch Snowflake Area

At each iteration a new triangle is added to each side of the previous iteration, so the number of new triangles added in the iteration $n$ is:

{displaystyle T_{n}=N_{n-1}=3cdot 4^{n-1}={frac {3}{4}}cdot 4^{n},.}

The area of each new triangle added in one iteration is 1/9 of the area of each triangle added in the previous iteration, so the area of each triangle added in the $n$ iteration is:

{displaystyle a_{n}={frac {a_{n-1}}{9}}={frac {a_{0}}{9^{n}}},.}

where $a 0$ is the area of the original triangle. The total new area added in the $n$ iteration is therefore:

{displaystyle b_{n}=T_{n}cdot a_{n}={frac {3}{4}}cdot {left({frac {4}{9}}right)}^{n}cdot a_{0}}

The total area of the snowflake after $n$ iterations is:

{displaystyle A_{n}=a_{0}+sum _{k=1}^{n}b_{k}=a_{0}left(1+{frac {3}{4}}sum _{k=1}^{n}left({frac {4}{9}}right)^{k}right)=a_{0}left(1+{frac {1}{3}}sum _{k=0}^{n-1}left({frac {4}{9}}right)^{k}right),.}

Collapsing the geometric sum gives:

{displaystyle A_{n}=a_{0}left(1+{frac {3}{5}}left(1-left({frac {4}{9}}right)^{n}right)right)={frac {a_{0}}{5}}left(8-3left({frac {4}{9}}right)^{n}right),.}

Area Boundaries

The area boundary is:

{displaystyle lim _{nrightarrow infty }A_{n}=lim _{nrightarrow infty }{frac {a_{0}}{5}}cdot left(8-3left({frac {4}{9}}right)^{n}right)={frac {8}{5}}cdot a_{0},,}

where |4/9| < 1.

Therefore, the area of the Koch snowflake is 8/ 5 of the area of the original triangle. Expressed in terms of the side length $s$ of the original triangle, that is:

{displaystyle {frac {2s^{2}{sqrt {3}}}{5}}.}

Fractal Properties

Accurate self-similitude of the Koch Snow Coup at all scales

The above characteristic, typical of many fractal curves, added to the fact that the curve gives the impression of having a certain thickness due to its constant changes of direction, suggests that this figure is, in some sense, not one-dimensional. For this we will use a generalization of the concept of dimension: the Hausdorff fractal dimension.

Its Hausdorff dimension must be between 1, that of a line, and 2, that of the plane. To find it, let's look at the last curve: If we enlarge (through a dilation) three times the section A'B' we get exactly the section AB. In the final curve, we would obtain section A'C, that is to say four times the initial section.

It is known that a dilation of ratio three multiplies the lengths by 3, the surfaces by 3² = 9, the volumes by 3³ = 27, and more generally, the "volume" of object of dimension d by 3^d. So we have 3^d = 4 for the Koch flake, which gives:

${displaystyle d={frac {ln 4}{ln 3}}approx 1,26186dots }$

The previous dilation dimension coincides in this case with the Hausdorff fractal dimension. The opposite-complementary configuration of a Koch snowflake or fractal snowflake is often called an anti-snowflake.

Variants of the Koch curve

There are multiple variants of the Koch curve, changing the 60° angle, the equilateral triangle for another polygon or the initial set.


Variant	Illustration	Construction
1D, angle 85°	Fractal de Cesàro (with 85°)	Variant of the Koch curve with angle between 60° and 90°. Dimension of approximate Hausdorff (85°): 1,7848.
1D, 90° angle	Type 1 von Koch Quadratic Curve	Variant of the Koch curve with 90° angle. Hausdorff Dimension: ln(5)/ln(3). 1,4649.
1D, 90° angle	Minkowski Sausage	Variant of the Koch curve with 90° angle. Hausdorff dimension: 1.5.
1D	(5;0.2)-curva of von Koch	Pentagonal variant of the Koch curve. Approximate Hausdorff Dimension: 1,37898.
2D, triangles	von Koch surface	Variant of the Koch curve over a 2D triangle.

Koch snowflake in Python language

Program using the turtle module, included in the Python standard library

import turtledef koch(size, n(c): # Koch curve drawing if n ♪ 0: turtle.fd(size) else: for angle in [chuckles]0, 60, -120, 60]: turtle.left(angle) koch(size/3, n-1)def main(level(c): # Three Koch curves are combined in a Koch snowflake turtle.setup(600, 600) turtle.penup.() turtle.drip(-200, 100) turtle.pendown() turtle.Think(2) koch(400, level) turtle.right(120) koch(400, level) turtle.right(120) koch(400, level) turtle.hideturtle()level = int(input("Introduce Koch's snowflake order:") # Enter ordermain(level)

Contenido relacionado

Más resultados...