Kirchhoff's laws

Kirchhoff's laws are two equalities that are based on the conservation of energy and charge in electrical circuits. They were first described in 1846 by Gustav Kirchhoff. They are widely used in electrical engineering and electronic engineering.

Both circuit laws can be derived directly from Maxwell's equations, but Kirchhoff preceded Maxwell and thanks to Georg Ohm his work became widespread. These laws are used to find currents and voltages at any point in an electrical circuit.

Kirchhoff's current law

The current that enters a node is equal to the current that leaves it. i₁ + i₄ =₂ + i₃

This law is also called Kirchhoff's law of nodes or first law and it is common to use the acronym LCK to refer to this law. Kirchhoff's current law tells us that:

This formula is also valid for complex circuits:

␡ ␡ k=1nI~ ~ k=0{displaystyle sum _{k=1}{n}{tilde {I}}_{k}=0}

The law is based on the principle of conservation of charge where the charge in coulombs is the product of current in amperes and time in seconds.

By definition, a node is a point in an electrical network at which three or more conductors converge.

This first law confirms the principle of conservation of electric charges.

Variant charge density

LCK is only valid if the charge density remains constant at the point where it is applied. Consider the current entering one sheet of a capacitor. If one imagines a closed surface around that sheet, current goes through the device, but not out, violating KCL. In addition, the current through a closed surface around the entire capacitor will meet the KCL entering one sheet is balanced by the current leaving the other sheet, which is what is done in circuit analysis, although it should be noted that there are a problem when considering a single sheet.

Maxwell introduced the concept of displacement current to describe these situations. The current that flows in the foil of a capacitor is equal to the increase in the accumulation of the load and is also equal to the rate of change of the electric flow due to the load (electric flow is also measured in Coulombs, as an electric charge in the SIU). This flow rate END END {displaystyle psi }That's what Maxwell called displacement current. ID{displaystyle I_{mathrm {D}}}:

ID=dEND END dt{displaystyle I_{mathrm {D} }={frac {dpsi}{dt}}}}

When the displacement current is included, Kirchhoff's law holds again. Displacement currents are not real currents since they do not consist of moving charges, they should be seen more as a correction factor to make LCK true. In the case of the capacitor sheet, the current entering the sheet is canceled by a displacement current leaving the sheet and entering the other sheet.

This can also be expressed in terms of the vector field by taking Ampere's Law of divergence with Maxwell's correction and combining Gauss's law, obtaining:

► ► ⋅ ⋅ J=− − ► ► ⋅ ⋅ ▪ ▪ D▪ ▪ t=− − ▪ ▪ ρ ρ ▪ ▪ t{displaystyle nabla cdot mathbf {J} =-nabla cdot {frac {partial mathbf {D} }{partial t}}}}{frac {partial rho }{partial t}}}}}

This is simply the equation of conservation of charge in integral form, it says that the current flowing through a closed surface is equal to the rate of loss of charge of the enclosed volume (Divergence Theorem). Kirchhoff's law is equivalent to saying that the current divergence is zero, for a time invariant p, or always true if the displacement current is included in J.

Kirchhoff's Stress Law

Kirchhoff Tension Act, in this case v₄= v₁+v₂+v₃. It does not take into account v₅ because it's not part of the mesh we're analyzing.

This law is also called Kirchhoff's second law, it is known as the stress law.

As with current, voltages can also be complex, like this:

␡ ␡ k=1nV~ ~ k=0{displaystyle sum _{k=1}^{n}{tilde {V}}_{k}=0}

This law is based on the conservation of a potential energy field. Given a potential difference, a charge that has completed a closed loop does not gain or lose energy upon returning to the initial potential.

This law is true even when there is resistance in the circuit. The validity of this law can be explained by considering that a charge does not return to its starting point, due to energy dissipation. A charge will simply end up on the negative terminal, instead of the positive. This means that all the energy given by the potential difference has been completely consumed by the resistance, which will transform it into heat. Theoretically, and since the voltages have a sign, this translates with a positive sign when going through a circuit from a higher potential to a lower one, and vice versa: with a negative sign when going through a circuit from a lower potential to a higher one..

In summary, Kirchhoff's voltage law has nothing to do with the gain or loss of energy of electronic components (Resistors, capacitors, etc.). It is a law that is related to the potential field generated by voltage sources. In this potential field, no matter what electronic components are present, the gain or loss of energy given by the potential field must be zero when a charge completes a loop.

Electric field and electric potential

Kirchhoff's stress law can be seen as a consequence of the principle of conservation of energy. Considering that electric potential is defined as a line integral, over an electric field, Kirchhoff's voltage law can be expressed as:

♫ ♫ CE⋅ ⋅ dl=0,{displaystyle oint _{C}mathbf {E} cdot dmathbf {l} =0,}

Which says that the line integral of the electric field around a closed loop is zero.

To return to a more special form, this integral can be "split" to get the voltage of a specific component.

Case study

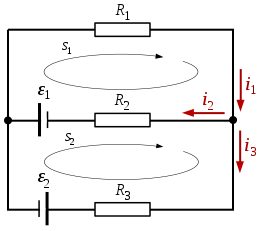
Assuming an electrical network consisting of two sources and three resistors, we have the following resolution: (before starting, it is necessary to clarify the sign convention: if I go through the mesh in favor of the current, the potential associated with the resistance is negative, otherwise it is positive If I go through the source and there is a rise in potential (from - to +), the emf is positive, otherwise it is negative.

According to Kirchhoff's first law (law of nodes), we have:

i1− − i2− − i3=0{displaystyle i_{1}-i_{2}-i_{3}=0,}

Kirchhoff's second law (mesh law), applied to the mesh according to the closed circuit s₁, gives us:

− − R2i2+ε ε 1− − R1i1=0{displaystyle -R_{2}i_{2}+varepsilon _{1}-R_{1}i_{1}=0}

Kirchhoff's second law (mesh law), applied to the mesh according to the closed circuit s₂, for its part:

− − R3i3− − ε ε 2− − ε ε 1+R2i2=0{displaystyle -R_{3}i_{3}-varepsilon _{2}-varepsilon _{1} +R_{2}i_{2}=0}

Because of the above, we have a system of equations with the unknown i1,i2,i3{displaystyle i_{1},i_{2},i_{3}}}:

{i1− − i2− − i3=0− − R2i2+ε ε 1− − R1i1=0− − R3i3− − ε ε 2− − ε ε 1+R2i2=0{displaystyle {begin{cases}i_{1}-i_{2}-i_{3}{3}{2}}{2}+varepsilon _{1}-R_{1}{1}{1}{1}{1}{1}{1}{1}{3}{3}-{3}{varepsilon

Given the magnitudes:

R1=100,R2=200,R3=300,ε ε 1=3,ε ε 2=4{displaystyle R_{1}=100, R_{2}=200, R_{3}=300,varepsilon _{1}=3, varepsilon _{2}=4},

the final solution would be:

{i1=11100i2=4275i3=− − 3220{displaystyle {begin{cases}i_{1}={frac {1}{1100}}}}{i_{2}={frac {4}{275}}}}{i_{3}=-{frac {3}{220}}}{end{cases}}}}}

It can be observed that i3{displaystyle i_{3}} has a negative sign, which means the direction of i3{displaystyle i_{3}} is inverse about what we have assumed at first (the direction of i3{displaystyle i_{3}} -in red-defined in the image).