ISO 216

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

The ISO 216 standard of the International Organization for Standardization (ISO) specifies the paper formats currently manufactured and used in most countries of the world.

History

Use of paper formats in the world.Use of ISO 216US-Letter

The ISO 216 format is derived from the German standard DIN 476, to which it is equivalent, except for the different tolerances allowed in each standard. The German standard DIN 476 was developed by the Berlin engineer Walter Porstmann, based in turn on sketches from the time of the French Revolution.

Before the dissemination of the standard, each country, territory and paper mill used its own sheet format, even with significant variations. However, at the beginning of the 20th century, discontent with this multiplicity of formats grew as it was impractical in many places. Thus, in 1910, the German chemist Wilhelm Ostwald developed a format designed to save space in libraries by standardizing the size of books. It was built requiring geometric similarity (ie, the aspect ratio of all sizes must be identical) and starting from the smallest format I, whose short side must measure 1 cm. The transition between sizes was made, as usual, by halving or doubling the sides; the aspect ratio was 1:2. This format did not become accepted due to incompatibility with existing formats.

Ostwald's idea was taken up by engineer Walter Porstmann, Ostwald's assistant. As an employee of the German Industry Standards Committee, he produced the DIN 476 standard, the formats of the series A to D, which are still valid except for the series D. It was introduced in Germany in 1923. These standard formats quickly established themselves at the national level. international, with the exception of some countries such as the United States and Canada, where other formats such as US-Letter (216 x 279 mm), US-Legal (216 x 356 mm) or US-Tabloid (279 x 431 mm) are used.)

The ISO 216 standard is equivalent to the Spanish standard UNE-EN-ISO 216.

Formula

The A-series drawing paper format is based on the following principles:

Different paper sizes have to have the same proportion between their larger and lower sides.
If two successive paper sizes are considered, one must have the double surface than the other and, in addition, dividing the larger format by half on its larger side, two copies are to be obtained equal to the previous format.
The A0 has a surface of a square meter.

Starting with a format with sides a and b, the upper format will have 2a by b, so that the proportion between its sides is the same, it will have to be fulfilled that:

{displaystyle {cfrac {b}{a}}={cfrac {2a}{b}}}

This is:

{displaystyle {cfrac {b^{2}}{a^{2}}}=2rightarrow quad left({cfrac {b}{a}}right)^{2}=2rightarrow quad {cfrac {b}{a}}={sqrt {2}}rightarrow quad b={sqrt {2}}cdot a}

If the ratio between the major and minor sides is a root of two, cutting a format into two equals will preserve this ratio.

If the A0 format has a surface area of one square meter, we will have:

{displaystyle left.{begin{array}{l}acdot b=1m^{2}\\b={sqrt {2}}cdot aend{array}}right}rightarrow quad acdot ({sqrt {2}}cdot a)=1m^{2}rightarrow quad {sqrt {2}}cdot a^{2}=1m^{2}rightarrow }

{displaystyle rightarrow quad a^{2}={cfrac {1m^{2}}{sqrt {2}}}rightarrow quad a={sqrt {cfrac {1m^{2}}{sqrt {2}}}}={cfrac {1m}{sqrt[{4}]{2}}}={cfrac {1}{1,189}};m=0,841;m}

Knowing the value of a, the calculation of b is immediate:

{displaystyle left.{begin{array}{l}acdot b=1m^{2}\\a=0,841mend{array}}right}rightarrow quad (0,841m)cdot b=1m^{2}rightarrow quad b={cfrac {1m^{2}}{0,841m}}=1,189m}

What we can summarize as a mnemonic rule that the DIN A0 format has as measurements:

{displaystyle DIN;A0quad left{{begin{array}{l}ancho={cfrac {1}{sqrt[{4}]{2}}};m\\largo={sqrt[{4}]{2}};mend{array}}right.}

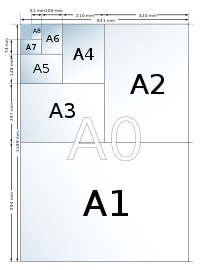
By dividing the longest side by two, we will successively obtain the different formats A1, A2, A3, A4...

Table of formats (ISO/DIN)

Illustration of series A

Symbol and size in millimeters. Deviations in measurements of ± 1.5 mm for measurements up to 150 mm, ± 2 mm for measurements up to 600 mm and ± 3 mm for larger measurements are tolerated. 2A0 and 4A0 do not exist in the ISO standard, but they are defined in the UNE, DIN and other standards.

ISO/DIN A÷E series, measurements in mm
	A-	B-	C-	D-	E-
4-0	1682 × 2378
2-0	1189 × 1682
- 0	841 × 1189	1000 × 1414	917 × 1297
-1	594 × 841	700 × 1000	648 × 917	545 × 779
-2	420 × 594	500 × 700	458 × 648	385 × 545
-3	297 × 420	350 × 500	324 × 458	272 × 385	400 × 560
-4	210 × 297	250 × 350	229 × 324	192 × 272	280 × 400
-5	148 × 210	175 × 250	162 × 229	136 × 192	200 × 280
-6	105 × 148	125 × 175	114 × 162	96 × 136	140 × 200
-7	74 × 105	88 × 125	81 × 114	68 × 96
-8	52 × 74	62 × 88	57 × 81
-9	37 × 52	44 × 62	40 × 57
-10	26 × 37	31 × 44	28 × 40

Main series UNE-EN-ISO 216 and DIN 476

The formats of the main series are named by the letter A and followed by a number. These numbers are correlative with each other. It should be noted that each of the sizes has half the surface of the previous one, so A1 is half A0, A4 half A3 and so on. This is achieved (see figure) thanks to the fact that the shortest dimension of an Ax is the longest of Ax+1; In other words, if a format is cut in half, the next format in the series is obtained.

Here are some of the most commonly used formats:

	Lamina cut	Gross lamina	Usable roll width
A0	841 × 1189	880 × 1230	900
A1	594 × 840	625 × 880	900 / 660
A2	420 × 594	450 × 625	900 / 660
A3	297 × 420	330 × 450	660 / 900
A4	210 × 297	240 × 330	660

A2 size is also known as "double A".

Previous UNE standard in Spain

Substitutions in Spain, of the usual sizes for DIN-A, and which were slightly larger:

DIN A1.
DIN A2 medium fold
DIN A3 small fold
DIN A4 α folio or half small fold
DIN A5 Δ quaartilla
DIN A6 Δ octavilla

Contenido relacionado

Más resultados...