Internal effort

Graphic representation of tensions or components of the tension tensor at a point of a body.

In structural engineering, the mechanical forces or section forces are physical magnitudes with units of force over area used in the calculation of prismatic parts such as beams or columns and also in the calculation of plates and sheets.

Definition

The internal stresses on a flat cross section of a structural element are defined as a set of forces and moments that are statically equivalent to the distribution of internal stresses over the area of that section.

So, for example, the stresses over a flat cross section Σ of a beam is equal to the integral of the stresses t over that flat area. Normally, a distinction is made between the forces perpendicular to the section of the beam (or thickness of the plate or shell) and those tangent to the section of the beam (or surface of the plate or shell):

• Normal effort (normal or perpendicular to the plane considered), is the one that is given by the result of normal tensions σ, that is, perpendicular, to the area for which we intend to determine the normal effort.
• Cutting effort (tangencial to the plane considered), is the one that is given by the result of cutting tensions τ, that is, tangential, to the area for which we intend to determine the cutting effort.

Section forces in beams and columns

For a mechanical prism or one-dimensional element the stresses are designated as:

• Normal effort (N_x)
• Total cut-off effort (V, T or Q)
  • Cutting force according to Y (V_and)
  • Cutting force according to Z (V_z)

Given an orthogonal axle system, in which the X axle coincides with the baricentric axis of a single-dimensional element with cross-section ${displaystyle scriptstyle Sigma }$ uniform, previous efforts are the result of tensions on each cross section:

${displaystyle N_{x}(x)=int _{sigma }sigma _{x} dA,qquad T_{y}(x)=int _{sigma }tau _{x},qquad T_{z}(x)=int _{sigma }tau _{xz}$

It is also common to call efforts:

• Moment torsor (M_x)
• Moment flector ${displaystyle left(M_{f}={sqrt {M_{z}^{2+}M_{y^{2}}}{2}}}{right)}$
  • Momento flector according to Z (M_z)
  • Moment flector according to Y (M_and)
• Bimomento (B_ω)

${displaystyle M_{x}(x)=int _{sigma }(tau _{xz}y-tau _{xy}z) dA,qquad M_{y}{x}{int _{sigma }zsigma _{x}{x$${displaystyle B_{omega }(x)=int _{Sigma }omega (y,z)sigma _{x} dA}$

Where ${displaystyle omega (y,z),}$ is the sectional linkage of the cross section.

Each of these efforts is associated with a certain type of tension:

• normal tension, normal effort (traction or compression) implies the existence of normal tensions, but these normal tensions can also be produced for a flector moment, according to the law of Navier. The bimoments also cause normal tensions due to the effect of the sectional alap.
• tangential tension, on the other hand the cutting efforts and the torsor moment imply the existence of tangential tensions τ.

Practical calculation of efforts in prisms

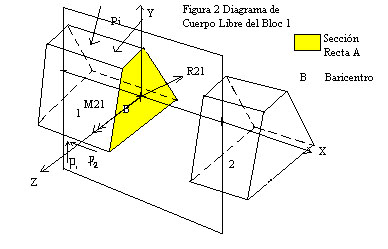
Let us consider the beam or mechanical prism that is observed in the first figure and suppose that it is linked to the rest of the structure in an isostatic way. We will also assume that active external forces act on this prism in the plane of its barycentric axis (or a straight line that joins the barycenters of all the straight cross sections of the prism).

The first step is to split the rigid into two smaller blocks. Blocks 1 and 2 of the figure are determined.

Next we will study block 1, where 2 reactive external forces appear acting (P₁ and P₁). As you can see, this block is not isostatically linked now, so in order for it to remain in equilibrium, there must be forces that balance it. These forces are also reactive forces and correspond to the action of block 2 on block 1. The reactive forces of block 2 on block 1 can be reduced to a force and a moment acting on the centroid of the straight section A. In fact these forces and moments are the resultant force and the resultant moment of the stress distribution over the straight area A.

Since we are dealing with the special case of active external forces acting on the plane of the barycentric axis, the moment and the force at which the reactive forces of block 2 are reduced on block 1, must be a force contained in said plane and a moment perpendicular to the same plane.

We will call the force R_2-1 of block 2 on the block and at the moment we will call it M_2-1 . The force R_2-1 can be broken down into a vertical component and a horizontal component in the plane that is contained. We will call R_2-1,y the force broken down in the vertical direction and R_2-1,x to the horizontally decomposed. Summarizing we have that the system of forces in equilibrium that is formed by:

• External active forces on block 1.
• Reactive forces P₁ and P₂.
• Reactive forces R_2-1,x, R_2-1,and and the moment M_2-1.

To the reactive forces R_2-1,x, R_{2-1, y} and currently M_2-1 are known as internal stresses. Y respectively represent the normal stress (N = R_2-1,x), the shear stress (Q = R_2-1,y) and the Bending Moment (M_f = M_2-1).

Calculation of stresses in prisms

In prismatic pieces subjected to compound bending (not deflected and without torsion), the calculation of the stresses is easy if the internal forces are known, for a symmetrical piece in which the center of gravity is aligned with the center of shear and with a total depth small enough compared to the length of the prismatic piece, in such a way that the Navier-Bernoulli theory can be applied, the stress tensor of a beam is given as a function of the internal forces by:

${displaystyle [T]_{xyz}={begin{bmatrix}sigma _{x} alientau _{y}{z}{z}\tau _{y}{sigma}{bmatrix}{bmatrix}}}}{{{sigmatrix}{sigma _{bmatrix}}}}}}}}}}$

Where normal (σ) and tangential (τ) tensions can be determined from internal efforts ${displaystyle N_{x},M_{y},M_{z},T_{y},T_{z};}$. If it is considered a system of main axes of inertia on the beam, considered as mechanical prism, the tensions associated with the extension, bending and cutting result to be:

${displaystyle sigma _{x}={frac {N_{x}}{A}{A}{A}{A}{I_{y}z}{I_{y}}{frac}{M_{z}}{I_{z}}}}}}}{Iqquad tau$

Where ${displaystyle k_{sec}}$ is the coefficient that relates the maximum cutter voltage and the average cutting voltage of the section. A criterion frequently used for metal beams is to verify that in all sections the following condition is verified:

${displaystyle sigma _{rm {cort}}={sqrt {sigma ^{2}+3(tau _{y}^{2}+tau _{z}{2}}}}}}}}}}{leq sigma$

Being ${displaystyle sigma _{u};}$ the final voltage or admissible voltage normally defined in terms of the elastic limit of the material. For prismatic pieces susceptible to panding the previous calculation does not lead to a safe design, since in that case the normal tension susceptible to developing in the piece is underestimated.

Stresses in plates and sheets

In a two-dimensional element, parameterized by two coordinates α and β, the number of stresses to be considered is greater than in one-dimensional elements:

• Membrane forces, according to the direction of the coordinated line α, ${displaystyle n_{alpha alpha },n_{alpha beta },}$according to the direction of the coordinated line β, ${displaystyle n_{beta beta },n_{beta alpha },}$.
• Cutting strengths: ${displaystyle v_{alpha },v_{beta },}$
• Bending efforts, ${displaystyle m_{alpha alpha },m_{alpha beta },m_{beta beta },m_{beta alpha },}$

Calculation of efforts in plates

In a sheet mainly subjected to bending in which despises deformation by cutter and membrane efforts are called foil of Love-Kirchhof, internal efforts are carazterized by two flange moments ${displaystyle m_{x},m_{y};}$ according to two mutually perpendicular directions and a torsor effort ${displaystyle m_{xy}}$. These efforts are directly related to the vertical arrow w(x, y) at each point by:

${cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cH00FFFFFF}{cH00FFFFFFFF}{cHFFFFFFFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFF}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cH00}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cH00}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cH00}{cH00}{cH$

Where:

${displaystyle nu ,}$It's Poisson's coefficient of plate material.

${displaystyle D=Hey^{3}/12(1-nu);}$, is the bending stiffness of the plate, being:

${displaystyle E;}$ Young's module of the plaque material.

${displaystyle h;}$ is the thickness of the plate.

Calculation of stresses in plates

The stresses on a plate are directly calculable from the above stresses:

${displaystyle {begin{cases}sigma _{xx}={cfrac {12z}{h^{3}}{m_{y}(x,y){sigma}{xx}{cH00}{cH00}{cH00}{cH00FF}{cH00FF}{cH00FFFF}{cH00FFFFFFFFFF}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00FFFFFFFFFFFF00}{cH00FFFFFFFFFFFFFFFF}{cH00}{cH00FFFFFFFFFFFFFFFFFF}{cH00}{cH00}{cH00}{cH00FF}{cH00FF00}{cH00FF00}{cH00}{cH00}{cH00FF}{c$