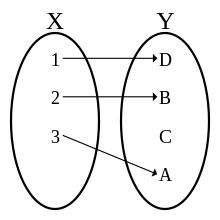
Injective function

ImprimirCitar

Example of non-superjective injective function.

In mathematics, a function:

{displaystyle {begin{aligned}f:X&longrightarrow Y\x&longmapsto f(x)end{aligned}}}

That's it. injecting, One by oneif to elements other than the whole $X$ (domain) they have different elements in the whole $Y$ (codomain) $f$ , that is, every element of the whole $Y$ has at most a preimage $X$ or, what is the same, in the whole $X$ There can be no two or more elements that have the same image.

For example, the function

{displaystyle {begin{aligned}f:mathbb {R} &to mathbb {R} \x&mapsto x^{2}end{aligned}}}

is not injective because value 4 can be obtained as ${displaystyle f(2)}$ and ${displaystyle f(-2)}$ but if the domain is restricted to positive real numbers (obtaining a new function ${displaystyle g:mathbb {R} ^{+}to mathbb {R} ^{+}}$ ) then if you get an injecting function you can perform a supreme calculation.

Definition

Sea $f$ a function whose domain is the whole $X$ , it is said that the function $f$ That's it. injecting Yes, for everything. $a$ and $b$ in $X$ Yeah. ${displaystyle f(a)=f(b)}$ then. ${displaystyle a=b}$ , this is ${displaystyle f(a)=f(b)}$ implies ${displaystyle a=b}$ . Equally, yes. ${displaystyle aneq b}$ then. ${displaystyle f(a)neq f(b)}$ . Symbolically,

{displaystyle forall ,a,bin X, f(a)=f(b)Longrightarrow a=b}

which is equivalent to its counter reciprocal

{displaystyle forall ,a,bin X, aneq bLongrightarrow f(a)neq f(b)}

To prove that a function is not injective, it is enough to find two different values of the domain, whose images in the codomain are equal.

Examples

For any set $X$ and subset ${displaystyle Ssubseteq X}$ , including map ${displaystyle Sto X}$ (which sends any element $sin S$ a himself) is injective. In particular, identity function ${displaystyle Xto X}$ is always injective (and indeed bi-yective).
Function ${displaystyle h:mathbb {R} to mathbb {R} }$ defined by ${displaystyle h(x)=x^{3}}$ It's injective.
Function ${displaystyle f:mathbb {R} to mathbb {R} }$ defined by ${displaystyle f(x)=2x+1}$ It's injective.
Function ${displaystyle g:mathbb {R} to mathbb {R} }$ defined by ${displaystyle g(x)=x^{2}}$ is not injective because (e.g.) ${displaystyle g(1)=1=g(-1)}$ . However, if $g$ is redefined in such a way that your domain is the set of non-negative real numbers ${displaystyle [0,+infty)}$ then. $g$ It's injective.
The exponential function ${displaystyle exp:mathbb {R} to mathbb {R} }$ defined by ${displaystyle exp(x)=e^{x}}$ It is injective (but not overyective, because it does not generate negative numbers, which have no relation to any value of x).
The natural logarithm function ${displaystyle ln:(0,+infty)to mathbb {R} }$ defined by ${displaystyle xmapsto ln x}$ It's injective.
Function ${displaystyle g:mathbb {R} to mathbb {R} }$ defined by ${displaystyle g(x)=x^{n}-x}$ is not injective, since ${displaystyle g(0)=g(1)=0}$ .

Yeah. $X$ and $Y$ are subsets of $mathbb{R}$ geometrically, a function ${displaystyle f:Xto Y}$ is injective if your graph is never intersected by a horizontal line more than once. This principle is known as the horizontal line test.

Cardinality and injectivity

Given two sets $A$ and $B$ among which there is an injective function $f:Ato B$ they have cardinals who fulfill:

${displaystyle {mbox{card}}(A)leq {mbox{card}}(B)}$

If there is also another injective application ${displaystyle g:Bto A}$ , then it can be proved that there is a bijective application between A and B.

Injectivity in Euclidean space

Given a function ${displaystyle mathbf {f}:Omega subset mathbb {R} ^{n}to mathbb {R} ^{n}}$ differential with continuity on a domain of euclid space n- dimensional conditions may be established and sufficient to decide when this function is injective. The theorem of reverse function gives a condition not enough for a differentiable function to be locally injective:

${displaystyle det Dmathbf {f} neq 0}$

where:

{displaystyle Dmathbf {f} }

is the Jacobin matrix of the function.

{displaystyle det(cdot)}

is the determining function.

This condition is not a sufficient condition to guarantee the injectivity of the function (in fact, it is not a necessary condition either). To find sufficient conditions, the displacement vector associated with the function is defined as the following vector field:

${displaystyle mathbf {u} (mathbf {x})=mathbf {f} (mathbf {x})-mathbf {x} in mathbb {R} ^{n}}$

This function is interpreted as the difference between the initial position of a point and the final position of your image. It can be shown that there is a constant $scriptstyle c(Omega)$ if it is fulfilled:

$<math alttext="{displaystyle max _{mathbf {x} in {bar {Omega }}}|Dmathbf {u} (mathbf {x})|=sup _{mathbf {x} in Omega }|Dmathbf {u} (mathbf {x})|maxx한 한 Ω Ω ! ! Du(x) =supx한 한 Ω Ω Du(x) .c(Ω Ω )≤ ≤ 1{displaystyle max _{mathbf {x} in {bar {omega }}}}}{mathbf {u} (mathbf {x})positive=sup _{mathbf {x} in omega }mathbf {u} (mathbf {x1}posi}mathbf}mathbf {x1mathbf<img alt="{displaystyle max _{mathbf {x} in {bar {Omega }}}|Dmathbf {u} (mathbf {x})|=sup _{mathbf {x} in Omega }|Dmathbf {u} (mathbf {x})|$

Where:

{displaystyle {bar {Omega }}}

, is the topological closing of the domain

Omega

Then the function is [globally] injective, it can be proved that $scriptstyle c(Omega) = 1$ if the domain $scriptstyle Omega$ is convex, while a non-convex domain requires $<math alttext="{displaystyle c(Omega)c(Ω Ω ).1{displaystyle c(Omega)} <img alt="{displaystyle c(Omega)$ .

Contenido relacionado

Más resultados...