Inclined plane

ImprimirCitar

Wheelchair Rampa, Hotel Montescot, Chartres, France

The inclined plane (also known as a ramp or slope) is a simple machine consisting of a flat surface that forms an acute angle with the ground and is used to raise bodies to a certain height. It has the advantage that a lower force is required than that used to lift said body vertically (thanks to the decomposition of forces), although the distance traveled must be increased and overcoming the force of friction.

Overview

Inclined plan used for education, Galileo Museum, Florence

Inclined plan and forces acting on the solid

An incline is a flat support surface inclined at an angle, with one end higher than the other, used as an aid in raising or lowering a load. The incline is one of six simple machines classics defined by Renaissance scientists. They are widely used to move heavy loads over vertical obstacles; examples range from a ramp used to load goods onto a truck, to a person walking on a pedestrian ramp, to a car or train going up a grade.

Moving an object down an incline requires less force than lifting it up, at the cost of an increase in distance traveled. Its mechanical advantage, the factor by which force is reduced, is equal to the ratio of the length of the inclined surface and the height it saves. Due to the principle of conservation of energy, the same amount of mechanical energy (work) is required to lift a given object a given vertical distance, regardless of friction losses, but the inclined plane allows the same work to be done with a given vertical distance. smaller force exerted over a greater distance.

The angle of friction,, also sometimes called the angle of repose, is the maximum angle at which a load can remain stationary on an inclined plane due to friction, without sliding down. This angle is equal to the arctengent of the coefficient of friction μ_s between the surfaces.

Two other simple machines are often considered to be derived from the inclined plane. The wedge can be thought of as either a moving inclined plane or two inclined planes connected at the base. The screw consists of a narrow inclined plane wrapped around a a cylinder.

The term can also refer to a specific application, such as a straight ramp dug into a steep hillside to allow goods to be transported up and down. It may include wagons on rails or pulled by a cable system; a funicular or cable railway, such as the Johnstown Inclined Plane.

The laws governing the behavior of bodies on an inclined plane were first enunciated by the mathematician Simon Stevin, in the second half of the century XVI.

To analyze the forces existing on a body located on an inclined plane, it is necessary to take into account the existence of several origins in them.

First, the existence of a force of gravity, also known as weight, which is the consequence of the mass should be considered (M) that has the body supported in the tilted plane and has a magnitude of M.g with a vertical direction and represented in the figure by the letter G.
There is also a normal force (N), also known as the reaction force exerted on the body by the plane as a result of the third law of Newton, is in a direction perpendicular to the plane and has an equal magnitude to the force exercised by the plane over the body. The figure is represented by N and has the same magnitude as F₂= M.g.cos α and opposite sense to it.
There is finally a friction force, also known as friction force (F_R), which is always opposed to the sense of movement of the body regarding the surface, and whose magnitude depends on both the weight and the superficial characteristics of the tilted plane and the surface in contact of the body that provide a coefficient of friction. This force must have a value equal to F₁=M.g.sen αTo keep the body in balance. In the case where F₁ was greater than the force of friction the body would slide down the tilted plane. Therefore to climb the body a force must be performed with a magnitude that equals or exceeds the sum of F₁ + F_R.

History

Stevin Demonstration

In 1586, the Flemish engineer Simon Stevin (Stevinus) deduced the mechanical advantage of the tilted plane by an argument that used a bead collar. He imagined two tilted planes of equal height but different earrings, placed back with back (up) as in a prism. A necklace with beads located at equal intervals is placed on the tilted planes, with a part hanging below. The beads that rest on the planes act as loads on the planes, supported by the tension force that experiences the string at point "T". Stevin's argument is as follows:

The chain must be still, in mechanical balance. If it were heavier on one side than on the other, and it would begin to slide to the right or to the left by its own weight, when each account had moved to the position of the previous account, the string would be indistinguishable from its initial position and would therefore continue to be unbalanced and slider. This argument could be repeated indefinitely, resulting in a perpetual circular mobile situation, which is absurd. Therefore, it remains stationary, with the forces on both sides of the point T (Upequal.
The part of the chain that hangs under the tilted planes is symmetrical, with equal number of accounts on each side. Exercises an equal force on each side of the rope. Therefore, this portion of the rope can be cut on the edges of the planes (points S and V)leaving only the beads resting on the tilted planes, and this remaining portion will still be in static balance.
Since the beads are located at equal intervals on the collar, the total number of accounts supported by each plane, the total load, is proportional to the length of the plane. Since the input support force, the tension in the collar thread, is the same on both sides, the mechanical advantage of each plane is proportional to its slanted length.

As Dijksterhuis pointed out, Stevin's argument is not completely strict. The forces exercised by the hanging part of the chain do not need to be symmetrical because the hanging part “does not need to keep its shape” when released. Even if the chain is released with a zero angular moment, the movement, including oscillations, is possible unless the chain is initially in its balance configuration, an assumption that would make the argument circular.

Inclined planes have been used since prehistoric times to move heavy objects. Inclined walkways and causeways built by ancient civilizations such as the Romans are examples of the earliest surviving inclined planes and show that they understood the value of this device to move loads uphill. The heavy stones used in ancient stone structures such as Stonehenge are believed to have been moved and set into place using inclined planes made of earth, although evidence of such temporary construction ramps is difficult to find. The pyramids of Egypt were built using inclined planes, and siege ramps allowed ancient armies to overcome fortress walls. The ancient Greeks built a 6 km (3.7 mi) long paved ramp, the Diolkos, to haul ships overland across the Isthmus of Corinth.

However, the inclined plane was the last of the six classical simple machines to be recognized as such. This is probably because it is a passive and immobile device (the charge is the moving part), and also because it occurs in nature in the form of slopes and hills. Although they understood its use for lifting heavy objects, the ancient Greek philosophers who defined the other five simple machines did not include the inclined plane. This view persisted among some later scientists; and as late as 1826 Karl von Langsdorf wrote that an inclined plane "... is no more a machine than the slope of a mountain". calculating the force required to push a weight up an incline (its mechanical advantage) was discussed by the Greek philosophers Hero of Alexandria (c. 10 - 60 CE) and Papus of Alexandria (c. 290 - 350 CE), but both were wrong in their resolution.

It wasn't until the Renaissance that the inclined plane was solved mathematically and classified with the other simple machines. The first correct analysis of the inclined plane appeared in the work of the enigmatic author of the 13th century Jordanus Nemorarius, although his solution of the This problem was apparently not communicated to other philosophers of the time. Gerolamo Cardano (1570) proposed the incorrect solution that the force to be applied is proportional to the angle of the plane. Later, at the end of the century XVI, Michael Varro (1584), Simon Stevin (1586) and Galileo Galilei (1592) published three correct solutions over ten years. Although it was not the first, the deduction of the Flemish engineer Simon Stevin, is the best known, due to its originality and the use of a string of beads (see sidebar). In 1600, the Italian scientist Galileo included the inclined plane in his analysis of simple machines in Le Meccaniche ("On Mechanics"), showing its simi underlying litude with the other machines as a force amplifier.

The first elementary rules for sliding objects with friction down an inclined plane were discovered by Leonardo da Vinci (1452-1519), but remained unpublished in his notebooks. They were rediscovered by Guillaume Amontons (1699) and Charles-Augustin de Coulomb (1785) developed them further. Leonhard Euler (1750) showed that the tangent of the angle of internal friction on an inclined plane is proportional to friction.

Applications

Inclined planes are widely used in the form of "ramps" to load and unload goods on trucks, ships and planes. Wheelchair ramps are used to allow people with reduced mobility to overcome vertical obstacles without exceeding their strength. Inclined escalators and conveyor belts are also forms of inclined plane. On a funicular or cable railway, a railway car is moved up an inclined plane on cables. Incline planes also allow both people and heavy and breakable objects to safely clear a vertical drop using the normal force of the plane to distribute the effect of gravity. Aircraft evacuation ramps allow people to quickly and safely reach the ground from the height of the passenger compartment of a commercial aircraft.

Use of ramps to load a car in a truck

Loading a truck on a boat using a ramp

Emergency evacuation branch of an aircraft

Wheelchair Rampa from a Japanese bus

Loading haul in a truck

Other inclined planes are built into permanent structures. Vehicle highways and railways have inclined planes in the form of gradual inclines, ramps, and causeways to allow vehicles to overcome vertical obstacles such as hills without losing traction on the road surface. Similarly, pedestrian paths and railways sidewalks have smooth ramps to limit their slope, in order to guarantee that pedestrians can maintain the necessary traction conditions. Inclined planes are also used as entertainment for people to slide down in a controlled manner, in slides, water ramps, alpine skiing and skating rinks.

Ground branch (right) built by the Romans in 72 AD to invade Masada, Israel

Rampa peatonal, Palacio do Planalto, Brasilia

Johnstown Inclined Plane, a funicular railway

Burma Road, Assam, India, from Burma to China (1945)

Inclined plans on a "skate" track

Terminology

Slope

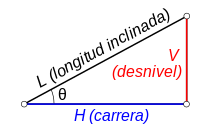
The effect of using an inclined plane depends on its slope, that is, its gradient or inclination. The lesser the incline, the greater the mechanical advantage and the less force required to lift a given weight. The slope s of a plane is equal to the difference in height between its two ends, or "unevenness", divided by its horizontal length, or "stroke". It can also be expressed by the angle formed by the plane with the horizontal, θ.

The inclined plane geometry is based on a rectangle triangle. Horizontal length (H) is sometimes called career, and the displacement in height measured in vertical (V) is called deseven

{displaystyle theta =arctan {bigg (}{frac {text{Desnivel}}{text{Carrera}}}{bigg)}=arctan {bigg (}{frac {text{V}}{text{H}}}{bigg)},}

Mechanical advantage

The mechanical advantage VM of a simple machine is defined as the ratio between the resultant force on the load and the applied force. For the inclined plane, the force to be overcome is just the gravitational force on the object loaded on the plane, its weight F_p. The applied force is F_i exerted on the object, parallel to the plane, to move it up the ramp. The mechanical advantages are...

{displaystyle mathrm {VM} ={frac {F_{p}}{F_{text{ap}}}}.,}

The mechanical advantage VM of an ideal frictionless incline is sometimes called the "ideal mechanical advantage" (VMI), while when friction is included it is called "true mechanical advantage" (VMR).

Frictionless inclined plane

Inclined instrumented plan used for the teaching of physics, around 1900. The weight of the left provides the strength to overcome F_p. The weight of the right provides the applied force F_ap pulling the roll up the plane

If there is no friction between the moving object and the plane, the device is called an "ideal inclined plane". This condition can be addressed if the object is rolling, such as a barrel, or resting on wheels. Due to the principle of conservation of energy, for a frictionless incline, the work done on the lifted load, W_res, equals the force applied times the distance traveled, W_ap

{displaystyle W_{rm {res}}=W_{rm {ap}},}

Work is defined as the force times the displacement that moves an object. The work done on the load is equal to its weight multiplied by the vertical displacement it goes up, which is the "lift" of the inclined plane.

{displaystyle W_{rm {res}}=F_{p}cdot {text{V}},}

The applied work is equal to the force F_ap exerted on the object multiplied by the length of the diagonal of the inclined plane.

{displaystyle W_{rm {ap}}=F_{rm {ap}}cdot {text{Long}},}

Substituting these values into the conservation of energy equation above and rearranging the addends

{displaystyle {text{VM}}={frac {F_{p}}{F_{rm {ap}}}}={frac {text{Long}}{text{V}}},}

To express the mechanical advantage as a function of the angle θ of the plane, it can be seen in the diagram above that

{displaystyle sin theta ={frac {text{V}}{text{Long}}},}

{displaystyle {text{VM}}={frac {F_{p}}{F_{rm {ap}}}}={frac {1}{sin theta }},}

Consequently, the mechanical advantage of a frictionless incline is equal to the reciprocal of the sine of the angle of inclination. The applied force F_ap from this equation is the force required to hold the load stationary on the incline or push it up at a constant velocity. If the input force is greater than the above value, the load will accelerate up the plane; if the force is less, it will accelerate downward.

Inclined plane with friction

Where there is friction between the plane and the load, such as with a heavy box sliding down a ramp, some of the work applied by the input force is dissipated as frictional heat, W _fric, so less work is done on the load. Due to conservation of energy, the sum of the work output and the energy losses due to friction is equal to the work input.

{displaystyle W_{text{ap}}=W_{text{fric}}+W_{text{res}},}

Therefore, more input force is required and the mechanical advantage is less than if there were no friction. With friction, the charge will only move if the net force parallel to the surface is greater than the opposing frictional force F_f to it. The maximum friction force is given by

{displaystyle F_{f}=mu F_{n},}

where F_n is the normal force between the charge and the plane, in the direction normal to the surface, and μ is the friction between the two surfaces, which varies with the material. When no input force is applied, if the inclination angle θ of the plane is less than a maximum value φ, the component of the gravitational force parallel to the plane will be too small to overcome friction and the charge will remain stationary. This angle is called the angle of internal friction and depends on the composition of the surfaces, but is independent of the weight of the load. The following shows that the tangent of the angle of repose φ is equal to μ

{displaystyle phi =arctan mu ,}

With friction, there is always some range of applied force F_ap for which the load is stationary, (i.e., neither slides up or down), whereas with a frictionless incline there is only a particular value of input force for which the load is stationary.

Analysis

Key: F_n = N = Normal force that is perpendicular to the plane, F_ap = f = applied force, F_p = mg = object weight, where m = mass, g = gravity

A load resting on an inclined plane, when considered as a free body, has three forces acting on it:

The force applied, F_ap exercised on the load to move it, which acts parallel to the tilted plane.
The weight of the load, F_pwhich acts vertically down
The force of the plane on the load, which can be broken down into two components:
- The normal force F_n of the plane tilted on the load that bears it. This is directed perpendicular (normal) to the surface.
- The friction force, F_f the plane on the load acts parallel to the surface, and always has an opposite direction to the movement of the object. It is equal to the normal force multiplied by the coefficient of friction μ between the two surfaces.

Using Newton's laws, the charge will be stationary or in constant motion if the sum of the forces on it is zero. Since the direction of the friction force is opposite for the case of movement uphill and downhill, these two cases must be considered separately:

Movement uphill: The total force on the load is to the side uphill, so the friction force is headed down on the plane, opposing the applied force.

Demonstration of mechanical advantage for movement uphill Balance equations for parallel and perpendicular forces to the plane are ${displaystyle sum F_{\|}=F_{rm {ap}}-F_{f}-F_{p}sin theta =0,}$ ${displaystyle sum F_{perp }=F_{n}-F_{p}cos theta =0,}$ Replacement ${displaystyle F_{f}=mu F_{n},}$ in the first equation ${displaystyle F_{rm {ap}}-mu F_{n}-F_{p}sin theta =0,}$ Solving the second equation to obtain ${displaystyle F_{n}=F_{p}cos theta ,}$ and replacing in the previous equation ${displaystyle F_{i}-mu F_{p}cos theta -F_{p}sin theta =0,}$ ${displaystyle {frac {F_{p}}{F_{rm {ap}}}}={frac {1}{sin theta +mu cos theta }},}$ Defining ${displaystyle mu =tan phi ,}$ ${displaystyle {frac {F_{p}}{F_{rm {ap}}}}={frac {1}{sin theta +tan phi cos theta }}={dfrac {1}{sin theta +{dfrac {sin phi }{cos phi }}cos theta }}={frac {cos phi }{sin theta cos phi +cos theta sin phi }},}$ Using the trigonometric identities of the sum of angles in the denominator,

The mechanical advantage is

{displaystyle mathrm {VM} ={frac {F_{p}}{F_{rm {ap}}}}={frac {cos phi }{sin(theta +phi)}},}

where

{displaystyle phi =arctan mu ,}

. This is the condition for the "appearing motion" up the tilted plane. If applied force F_ap is greater than the one given by this equation, the load will move up in the plane.

Movement downhill: The total force on the load is to the side downhill, so the friction force is headed up the plane.

Demonstration of mechanical advantage for movement downhill Balance equations are ${displaystyle sum F_{\|}=F_{rm {ap}}+F_{f}-F_{p}sin theta =0,}$ ${displaystyle sum F_{perp }=F_{n}-F_{p}cos theta =0,}$ Replacement ${displaystyle F_{f}=mu F_{n},}$ in the first equation ${displaystyle F_{rm {ap}}+mu F_{n}-F_{p}sin theta =0,}$ Solving the second equation to obtain ${displaystyle F_{n}=F_{p}cos theta ,}$ and replacing in the previous equation ${displaystyle F_{rm {ap}}+mu F_{p}cos theta -F_{p}sin theta =0,}$ ${displaystyle {frac {F_{p}}{F_{rm {ap}}}}={frac {1}{sin theta -mu cos theta }},}$ Substituting ${displaystyle mu =tan phi ,}$ and simplifying as above ${displaystyle {frac {F_{p}}{F_{rm {ap}}}}={frac {cos phi }{sin theta cos phi -cos theta sin phi }},}$ Using another list of trigonometric identities in the denominator,

The mechanical advantage is

{displaystyle mathrm {VM} ={frac {F_{p}}{F_{rm {ap}}}}={frac {cos phi }{sin(theta -phi)}},}

This is the condition for the impending movement down the plane; if the applied force F_i is less than the one given in this equation, the load will slide down the plane. There are three cases:

$<math alttext="{displaystyle theta θ θ .φ φ {displaystyle thetaphi ,} <img alt="{displaystyle theta$ : The mechanical advantage is negative. In the absence of applied force, the load will remain immobile and requires some negative applied force (subside) to slide down.
${displaystyle theta =phi ,}$ : The hole of rest. The mechanical advantage is infinite. Without applied force, the load will not slide, but the slightest negative force (subject to the table) will make it slide.
$phi ,}" xmlns="http://www.w3.org/1998/Math/MathML">θ θ ▪φ φ {displaystyle theta /2005phi ,}phi ,}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1aec7466157fd11437c1c9ff6a695a5f349affba" style="vertical-align: -0.671ex; width:5.961ex; height:2.509ex;"/>$ : The mechanical advantage is positive. In the absence of applied force, the load will slide down the plane and requires a positive force (top) to keep it still.

Mechanical advantage using power

Clave: N = Normal force that is perpendicular to the plane, p=mg, where m=masa, g=gravedad, and θ(theta) = Flat tilt angle

The mechanical advantage of an incline is the ratio between the weight of the load on the ramp and the force required to move it up. If energy is not dissipated or stored in the movement of the load, this mechanical advantage can be calculated from the dimensions of the ramp.

To demonstrate this, let r be the position of a wagon on a ramp with an angle θ above the horizontal, given by

{displaystyle mathbf {r} =R(cos thetasin theta),}

where R is the distance on the ramp. The speed of the car on the ramp is now

{displaystyle mathbf {v} =V(cos thetasin theta).}

Because there are no losses, the power used by the force "F" to move the load up the ramp is equal to the resultant power, which is the vertical lift of the weight "p" of the load.

The power input driving the wagon up the ramp is given by

{displaystyle P_{mathrm {ap} }=FV,!}

and the resulting power is

{displaystyle P_{mathrm {res} }=mathbf {p} cdot mathbf {v} =(0,p)cdot V(cos thetasin theta)=pVsin theta.}

Equating the applied power and the resulting power, the mechanical advantage is obtained as

{displaystyle mathrm {VM} ={frac {p}{F}}={frac {1}{sin theta }}.}

The mechanical advantage of an inclined ramp can also be calculated from the ratio of the length of the ramp L to its vertical height V, because the sine of the ramp angle is given by

{displaystyle sin theta ={frac {V}{L}},}

therefore,

{displaystyle mathrm {VM} ={frac {p}{F}}={frac {L}{V}}.}

Disposition of the Liverpool Minard tilted plane cable drive system

Example: if the height of a ramp is V = 1 meter and its length is L = 5 meters, then the mechanical advantage is

{displaystyle mathrm {VM} ={frac {p}{F}}=5,}

which means that a force of 20 kg will lift a load of 100 kg.

The Liverpool Minard inclined plane has dimensions of 1804 meters by 37.50 meters of unevenness, which provides a mechanical advantage of

{displaystyle mathrm {VM} ={frac {p}{F}}=1804/37.50=48.1,}

so a tensile force of 100 kp in the cable will lift a load of 4810 kp. The degree of this slope is 2%, which means that the angle θ is small enough that sin θ=tan θ.

Contenido relacionado

Más resultados...