Incenter

A triangle and its incenter I. The red lines are the bisectrices of the three internal angles.

Incenter I

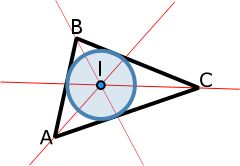
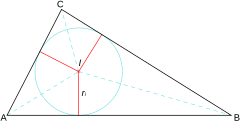
The Incenter of a triangle (marked with the letter I on the graph) is the point where the three bisectors of its internal angles intersect. Equidistant from the three sides, and therefore, is the center of the circle inscribed in the triangle, tangent to its three sides.

Along with the centroid, circumcenter, and orthocenter, it is one of the four notable points of the triangle known to the ancient Greeks, and the only one not lying on Euler's line.

In the Encyclopedia of Triangle Centers (the work of American mathematician Clark Kimberling) X(1) is designated as the first entry in the list of centers. It is the identity element of the multiplicative group of the centers of the triangle.

For polygons with more than three sides, the incenter only exists in tangential polygons - that is, those that have an incircle that is tangent to all sides of the polygon. In this case, the incenter is the center of this circle and is equidistant from all sides.

Cartesian coordinates

The Cartesian coordinates of the incenter can be deducted from the coordinates of the three vertices of the triangle A, B and C. If the vertices have coordinates ${displaystyle (x_{a},y_{a}),}$, ${displaystyle (x_{b},y_{b}),}$and ${displaystyle (x_{c},y_{c}),}$and the opposite sides have lengths ${displaystyle a,}$, ${displaystyle b,}$and ${displaystyle c,}$The incenter will have coordinates ${displaystyle (x_{I},y_{I}),}$:

${displaystyle (x_{I},y_{I})={frac {a(x_{a},y_{a})+b(x_{b},y_{b}{b}{c(}{c}{c}{c}{c(}{c}{c}{c(}{c)}{c(}{c}{c}{c}{c}{c(},y}{c)}{a !$

Demonstration

The inner bisectrices of a triangle as a cevian straight. Indeed, By the the theorem of the bisectriz, applied to the angles bisectrices ${displaystyle {widehat {A}}}$ and ${displaystyle {widehat {B}}}$You have to. ${displaystyle {dfrac {c}{b}}={dfrac {BP}{PC}}}={dfrac {BP}{BC-BP}}}={dfrac {BP}{a-BP}}}}},$ ${displaystyle {dfrac {c}{a}}{dfrac {AQC}}}={dfrac {AQ}{AC-AQ}}={dfrac {AQ}{b-AQ}}}}}}}$ resulting ${displaystyle BP={dfrac}{b+c}}},qquad AQ={dfrac {bc}{a+c}}}}$ Be vectors ${displaystyle {overrightarrow {BP}}}}$ and ${displaystyle {overrightarrow {AQ}}}$ Then: ${cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}}{cHFFFFFFFF}{cHFFFFFF}{cHFFFF}{cHFFFF}{cH00}{cH00}{cHFFFFFFFFFFFFFFFF}{cH00}{cH00}}{cH00}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFF$ For vectors ${displaystyle {overrightarrow {AI}}}$ and ${displaystyle {overrightarrow {BI}}}$ There are real numbers ${displaystyle lambda }$ and ${displaystyle mu }$ with ${displaystyle {overrightarrow {AI}}=lambda {overrightarrow {AP}}}}$ and ${displaystyle {overrightarrow {BI}}{overrightarrow {BQ}}}}$. So, expressing the vector ${displaystyle {overrightarrow {AI}}}$ of these two forms, ${displaystyle {overrightarrow {AI}}=lambda {overrightarrow {AP}}}}$ and ${displaystyle {overrightarrow {AI}}={overrightarrow {AB}}}+{overrightarrow {BI}}$You have to: ${bleep} !$ Now, given the linear independence of the vectors ${displaystyle {overrightarrow {AB}}}$ and ${displaystyle {overrightarrow {BC}}}$ Then: ${displaystyle left{begin{array}{rcl}lambda &= fake1-mu +{dfrac {mu c}{a+c}{{dfrac} {lambda c}{b+c}}}{ fake{dfrac {mu c}{a+c}{a+c}}}{end{array}}}}{ !$ The previous system, which is a linear system, has the solutions ${displaystyle lambda ={dfrac {b+c}{a+b+c}}qquad mu ={dfrac {a+c}{a+b+c}}}}}}}}}$ Finally, $♪♪$

Trilinear coordinates

The trilinear coordinates of the incenter are

${displaystyle 1:1:1}$

The collection of triangle centers presents a group structure when its coordinates are expressed in the trilinear system with respect to the product operation. In this group, the incenter is the identity element.

Barycentric coordinates

The barycentric coordinates of the incenter are

${displaystyle a:b:c}$

where ${displaystyle a}$, ${displaystyle b}$and ${displaystyle c}$ are the lengths of the sides of the triangle, or in equivalent form (using the theorem of the breasts) can be defined as

${displaystyle sin(A):sin(B):sin(C)}$

where ${displaystyle A}$, ${displaystyle B}$and ${displaystyle C}$ are the angles of the three vertices of the triangle.

Incenter properties

Distances to vertices

Calling the incenter of triangle ABC as I, the distances from the incenter to the vertices, according to the lengths of the sides, obey the equation

${displaystyle {frac {IAcdot IA}{CAcdot AB}}}{cdot IB}{ABcdot BC}}} +{frac {ICcdot IC}{BCcdot CA}}}{1}$

Additionally,

${displaystyle IAcdot IBcdot IC=4Rr^{2}$

where R and r are the radii of the circumscribed and inscribed circles respectively.

Distance at vertex A.

1. Knowing the angle A and the radius r

${displaystyle d(I,A)=rcdot csc{frac {A}{2}}}}}}$ → (1), r radius of the inscribed circle.

2. Knowing the three sides.

${displaystyle d(I,A)={sqrt {frac {bc(p-a)}{p}}}}}}}$ where a, b and c are the lengths of the sides and ${displaystyle p={frac {a+b+c}{2}}}}}$ It's the semi-perimeter.

To derive this cyclic formula, equate pr with Heron's formula. Solve for cos A from the formula provided by the law of cosines and find the sin of A/2, as well as the cosecant of A/2. Replace r and csc A/2 in the above formula (1).

Other centers

The distance between the incenter and the centroid is less than one-third the length of the longest median of the triangle.

According to Euler's geometric Theorem, the distance between the incenter I and the circumcenter O raised to the square, is given by

${displaystyle OI^{2}=R(R-2r),}$

where R and r are the circumradius and inradius respectively; consequently, the circumradius is at least twice the inradius (being exactly twice only in the case of the equilateral triangle).

The distance from the incenter to the center N of the circle of the nine points is

${displaystyle IN={frac {1}{2}}}(R-2r) implied{frac {1}{2}{2}R}$

The squared distance between the incenter and the orthocenter H is

${displaystyle IH^{2}=2r^{2}-4R^{2}cos Acos Bcos C}$

There are inequalities that state that:

${displaystyle IG ingredientHG,quad IH visHG,quad IG visIO,quad 2IN$

The incenter is the Nagel point of the medial triangle (the triangle whose vertices are the midpoints of the sides) and is located inside this triangle. Conversely, the Nagel point of any triangle is the incenter of its anticomplementary triangle.

The incenter is located inside a disk whose diameter joins the centroid G and the orthocenter H (the orthocentroidal disk), but cannot coincide with the center of the nine points, whose position is fixed at 1/4 along the diameter (closest to G). No other point within the orthocentroidal disk is the incenter of any of the singular triangles.

Euler line

The Euler line of a triangle passes through its circumcenter, centroid, and orthocenter, as well as other notable points. The incenter does not generally lie on the Euler line; except for isosceles triangles, in which case the Euler line coincides with the triangle's axis of symmetry and contains all its centers.

Determining the distance from the incenter to the Euler line d; to the length of the largest median v; to the length of the longest side of triangle u; to circumradius R; to the length of the Euler line segment from the orthocenter to the circumcenter e; and to the semi-perimeter s; we have the following inequalities:

${displaystyle {frac {d}{s}}}{s}}{frac {d}{s}}{frac}}{d}{s}}{frac {1}}}}}}}}}$

${displaystyled}{frac {1}{3}e}$

${displaystyled}{frac {1}{2}R}$

Area and perimeter divisions

Any line that divides a triangle into two parts of equal area and equal perimeter (both conditions occur simultaneously), passes through its incenter. There may be one, two, or three of these lines for any given triangle.

Relative distance of the points of a bisector

Sea X a point of the angle bisectr A. Then when X = I (incenter) maximizes or minimizes the quotient ${displaystyle {tfrac {BX}{CX}}}}$ along the bisector.