Icosahedron

Animation of one of the developments of the regular icosaedro.

An icosahedron is a polyhedron with twenty faces. There are infinitely many variants of the icosahedron, but only two regular icosahedrons: the convex regular icosahedron, one of the Platonic solids; and the great icosahedron, non-convex and one of the Kepler-Poinsot solids.

Internal radius

The radius of an inscribed sphere (tangent to the faces of the icosahedron) is

${displaystyle r_{i}={frac {a}{12}}{sqrt {3}}}left(3+{sqrt {5}}{right)approx 0.75576131cdot a}$

Angle

The angle formed by the vectors that go from the center to two adjacent vertices is constant and is worth:

${displaystyle {text{angle}}=2cdot arcsin left({frac {1}{2cdot 0.9510565163}}right)approx 1.10714872 {text{rad}}}}}}$

Volume and Area

Given a regular icosahedron with edge a, its volume V can be calculated using the following formula:

${displaystyle V={frac {5}{12}}}left(3+{sqrt {5}}}}right)cdot a^{3}}}}$
(approximately 2,18·a3)

And the total area of their faces A (which is 20 times the area of one of them, A_c), using:

${displaystyle A=20cdot A_{c}=20cdot {frac {sqrt {3}{4}}}cdot a^{2}=5{sqrt {3}}}cdot a^{2}}}$
(approximately 8,66·a2)

Cartesian coordinates and structure

Icosaedro regular spinning

The following Cartesian coordinates define the vertices of an icosahedron centered at the origin:

(0, ±1, ±φ)

(±1, ±φ, 0)

(±φ, 0, ±1)

Where φ = (1+√5)/2 is the golden ratio (also written as τ). Note that the vertices of an icosahedron form groups of three orthogonal golden rectangles. The icosahedron contains 15 golden rectangles: each rectangle contains two opposite edges. This is because two sides of the rectangle are the edge of the icosahedron and the other two are the diagonals of two parallel regular pentagons rotated 180 degrees. The diagonal of the regular pentagon is in golden ratio with the side of the pentagon, which in this case is the edge of the icosahedron.

The icosahedron, despite being formed by 20 equilateral triangles, can be considered as the union of 12 internal regular pentagons. The intersection of the pentagons with each other originates the 30 edges that make up the icosahedron. The 12 regular pentagons mentioned determine the faces of the great dodecahedron, one of the Kepler-Poinsot solids.

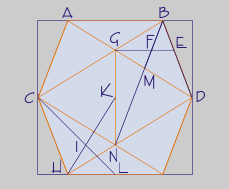
Golden ratios in the icosahedron

Figure of regular icosaedron vertex (3.3.3.3)

The 12 inner pentagons that constitute the icosahedron determine the faces of the great dodecahedron.

In the icosahedron we can find several times the golden ratio. In the image on the left you can see some golden ratios present in the icosahedron:

${displaystyle phi }$

${displaystyle =CD/AB=EG/FG=AD/GD}$ ${displaystyle =KH/IK=GD/AG=BN/MN}$ ${displaystyle =CL/CI=AH/GN=MN/BM}$ ${displaystyle =BM/BF=FG/EF=BF/FM}$ ${displaystyle = IK/HI=GD/MD=CI/LI}$ ${displaystyle =MD/GM=BC/CG=CG/GB}$

Geometric relationships

The icosaedro as tetraedro romo.

There are distortions of the icosahedron that, although not regular, are nevertheless vertex-uniform. These are invariant on the same rotations as the tetrahedron, and are somewhat analogous to the snub cube and snub icosidodecahedron, including some shapes that are chiral and others with pyritohedral symmetry, and that have different planes of symmetry than the tetrahedron. The icosahedron has 58 stellations (59, if the icosahedron is included), including one of the Kepler-Poinsot solids (the great icosahedron) and some regular compound stellations.

The 12 edges of an octahedron can be divided in the golden ratio so that the resulting vertices define an icosahedron. If the icosahedron is inscribed in a cube, the edges of the inscribed icosahedron are in golden ratio with the edges of the cube.

The icosahedron is unique among the Platonic solids in having a dihedral angle greater than 120°. Consequently, just as hexagons have angles equal to 120° and cannot be used as faces for a convex regular polyhedron because such a construction would not satisfy the requirement that at least three faces meet at a vertex and leave a positive defect. to fold in three dimensions, the icosahedron cannot be used as a cell for a regular convex polychore because, for the same reason, at least three cells must meet on one edge and leave a positive defect for folding in four dimensions (in general for a convex polytope in n dimensions, at least three faces must meet on an edge and leave a positive defect for folding in n-dimensional space). However, when combined with appropriate cells having smaller dihedral angles, the icosahedron can be used as a cell in semiregular polychores (for example, rounded 24-cell), just as hexagons can be used as faces of semiregular polyhedra (for example, the truncated icosahedron). Finally, non-convex (concave) polytopes do not need the same stringent requirements as convex polytopes, and icosahedrons are, in effect, the cells of the 120-cell icosahedron, one of ten regular non-convex polychores.

An icosahedron can be considered as a gyroelongated pentagonal dipyramid. It can be decomposed into a gyroelongated pentagonal pyramid and a pentagonal pyramid or into a pentagonal antiprism and two equal pentagonal pyramids.

The icosahedron can also be called a blunt tetrahedron, rounding a regular tetrahedron produces a regular icosahedron. Alternatively, using the nomenclature for rounded polyhedra referring to the snub cube as snub cuboctahedron (cuboctahedron = rectified cube) and the snub dodecahedron as snub icosidodecahedron (icosidodecahedron = rectified dodecahedron), the icosahedron may be called snub octahedron (octahedron = rectified tetrahedron).

Icosahedron vs. Dodecahedron

Despite appearances, when an icosahedron is inscribed in a sphere it occupies less volume of the sphere (60.54%) than a dodecahedron inscribed in the same sphere (66.49%).^{[citation required]}

Symmetry

A regular icosahedron has six axes of symmetry of order five, the lines that join the opposite vertices; fifteen axes of symmetry of order two, the lines that join the centers of opposite edges; fifteen planes of symmetry, containing each pair of opposite coplanar edges; and a center of symmetry. This makes this field have a total symmetry order of 120: 2x(6x5+15x2).

The above symmetry elements define one of the icosahedral symmetry groups, the so-called I_h according to Schöenflies notation.

The icosahedron also has ten axes of symmetry of order three: the lines that join the centroids of each pair of opposite faces.

By subdividing each face of the icosahedron into triangles, geodesic domes can be constructed.

Applications, examples and natural forms

The Platonic solids have been known since antiquity and it is known that at least the Pythagorean sects of the 5th and 4th centuries BC attributed metaphysical, numerological or simply religious properties to them. Regarding the regular icosahedron, it had been used during Ancient Rome for the manufacture of dice, as evidenced by two twenty-sided dice from Ancient Rome preserved in the British Museum. It is not known, however, for what activity they were manufactured. these dice, whether for a game or for any other activity.

The twenty-sided die (abbreviated as “D20”) became popular in the 1960s and 1970s as it was used more and more frequently by so-called war games, which in those years were beginning to see a big success. A few years later, in 1974, the first role-playing game to be commercialized, Dungeons & Dragons, based its game system on the use of a twenty-sided dice. Since then the twenty die has had and continues to have an important role in many role-playing games. Twenty-sided dice can be numbered "0" through "9" twice (in order to be used as a hundred-sided die) but in 1980 ten-sided dice were invented to be used this way so today in Today most versions of the twenty dice are numbered from "1" to "20".

Circogonia icosahedraA species belonging to the radio station.

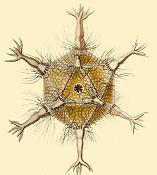
Many viruses, such as herpes, have the shape of an icosahedron. Viral structures are built on the basis of identical protein units repeated several times and the icosahedron is the simplest way to assemble using these subunits. A regular polyhedron is used because it can be built by a single protein unit by using it over and over again; this saves space for the viral genome. Also some protists, especially some radiolarians, have an icosahedral shape, such as Circogonia icosahedra.

The inner die of a magic 8 ball that has 20 printed answers to yes/no questions is a regular icosahedron.

If each edge of an icosahedron is replaced by a one-ohm resistor, the resistance between opposite vertices is 0.5 ohms, and between adjacent vertices is 11/30 ohms.

The Fuller projection (or Dymaxion map, created by Richard Buckminster Fuller) is a gnomonic projection based on the icosahedron.

The icosahedron is the shape of the Dogic, a toy similar to a Rubik's cube.

An icosahedron appears as an enemy in Kirby 64, it is known as Miracle Matter. Also in the Pokémon Platinum video game is an icosahedron-shaped object called the Griseous Orb. Another is in the Cuphead Video Game, where a projectile thrown by Pip and Dot is in the shape of an Icosahedron.