Hyperbola

AjustarCompartirImprimirCitar

The hipperbola asymptotes are shown as blue discontinuous lines that are cut in the middle of the hipérbola (red curves), C. The two focal points are called F₁ and F₂, the black line connecting the vertices is the cross-sectional axis. The thin black perpendicular line passing through the center is the conjugated axis. The two thick black lines parallel to the conjugated axis (so perpendicular to the transversal axis) are the two guidelines, D₁ and D₂. Eccentricity e (e/2003/1), is equal to the quotient between distances (in green) from a point P from the hyperbola to one of the foci and its corresponding guideline. The two vertices are in the cross axis at a distance ±a regarding the center.

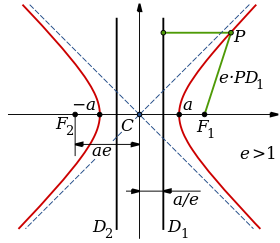
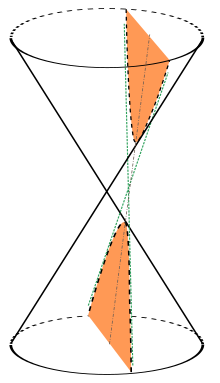
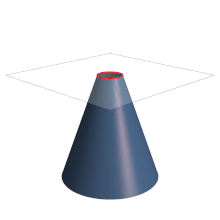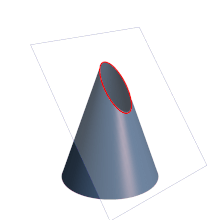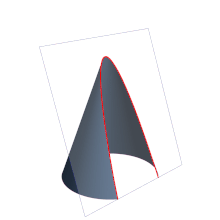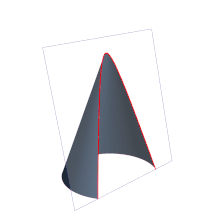
A hyperbola (from the Greek ὑπερβολή) is an open curve with two branches, obtained by cutting a right cone through a plane not necessarily parallel to the axis of symmetry, and with an angle less than that of the generatrix about the axis of revolution. In analytic geometry, a hyperbola is the locus of points in a plane such that the absolute value of the difference of their distances to two fixed points, called foci, is equal to the distance between the points. vertices, which is a positive constant. Being this constant less than the distance between the foci.

Etymology

Conical sections.

Hyperbola comes from the Greek word ὑπερβολή (excess), and is cognate with the literary term hyperbole.

History

Due to the inclination of the court, the plane of the hyperbola intersectes both branches of the cone.

According to tradition, conic sections were discovered by the Greek geometer and mathematician Menechmus (380 B.C.- 320 B.C.), in his study of the problem of doubling the cube, through which he proved the existence of a solution using the cutting a parabola with a hyperbola, which is later confirmed by Proclus and Eratosthenes, also geometers.

However, the first to use the term hyperbola was Apollonius of Perge in his treatise Conics, considered the masterpiece on the subject of Greek mathematics, and where the study of tangents to conic sections is developed.

Equations of the hyperbola

Canonical equations in Cartesian coordinates

The hyperbola whose center is at the origin of coordinates ${displaystyle O(0,0),}$ is representative by one of the following equations commonly referred to as canonical equation or normal form of the equation of a hyperbola:

(1) ${displaystyle {frac {x^{2}}{a^{2}}}-{frac {y^{2}}{b^{2}}}=1Rightarrow b^{2}x^{2}-a^{2}y^{2}=a^{2}b^{2}}$

(2) ${displaystyle {frac {y^{2}}{a^{2}}}-{frac {x^{2}}{b^{2}}}=1Rightarrow b^{2}y^{2}-a^{2}x^{2}=a^{2}b^{2}}$

In these equations $a$ , $b$ and $c$ , represent the transverse, conjugated and focal semies, respectively. The equation (1) represents the hyperbolas whose focal axis is colineal to the axis $x$ and the2) for those who are about the axis $y$ . In the first equation, the focus is on ${displaystyle F(pm c,0)}$ and the vertices in ${displaystyle V(pm a,0)}$ . In the second, the focus is on ${displaystyle F(0,pm c)}$ and the vertices in ${displaystyle V(0,pm a)}$ . In any case, the relationship between the three semies is given by equality:

(3) $c^{2}=a^{2}+b^{2}$

However, it should be noted that, unlike the case of ellipse, not necessarily $b}" xmlns="http://www.w3.org/1998/Math/MathML">a▪b{displaystyle a vocabularyb}b}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/83fc0063781fb9bf4ec7608b2fd11ed6d5b05a13" style="vertical-align: -0.338ex; width:5.326ex; height:2.176ex;"/>$ .

Equations of a hyperbola with center at the point C. ( h what ) {displaystyle C(h,k)}

As in the previous case, the equation assumes one of the following forms:

(4) ${displaystyle {frac {(x-h)^{2}}{a^{2}}}-{frac {(y-k)^{2}}{b^{2}}}=1}$

(5) ${displaystyle {frac {(y-k)^{2}}{a^{2}}}-{frac {(x-h)^{2}}{b^{2}}}=1}$

The equation (4) corresponds to hyperboles whose focal and greater axis are parallel to the axis $x$ in which the vertex is in ${displaystyle V(hpm a,k)}$ and focus on ${displaystyle F(hpm c,k)}$ . The equation (5) is that of the hipérbolas whose focal and greater axis are parallel to the axis $y$ in which the vertices are located ${displaystyle V(h,kpm a)}$ and focus on ${displaystyle F(h,kpm c)}$ .

Eccentricity

Conical sections.

Eccentricity $e$ of a hyperbola is a value defined as:

{displaystyle e={frac {c}{a}}}

where:

$c$ represents half the distance of the focal axis.
$a$ represents half the distance from the main axis.

Since $c$ is a higher value than $a$ The eccentricity of a hyperbole is always greater than 1.

General equation of the hyperbola

The general equation of a hyperbola is the following:

(5) ${displaystyle Ax^{2}-Cy^{2}+Dx+Ey+F=0}$

If the coefficients $A$ and $C$ are of different signs, not null and $0}" xmlns="http://www.w3.org/1998/Math/MathML">A▪0{displaystyle ARV0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/232a94dbd97f2ce670d4987c5ad8ad82b072861b" style="vertical-align: -0.338ex; width:6.004ex; height:2.176ex;"/>$ and $0}" xmlns="http://www.w3.org/1998/Math/MathML">C▪0{displaystyle C/2003/0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/c84d4126c6df243734f9355927c026df6b0d3859" style="vertical-align: -0.338ex; width:6.027ex; height:2.176ex;"/>$ , then (5) represents the general equation of a hyperbola whose axes are parallel or colinear to the coordinated axes or a pair of straights that are cut.

Demo

In the equation (5) are separated the variables in $x$ and $y$ converting to $A$ and $C$ in common factors:

(6) ${displaystyle Aleft(x^{2}+{frac {D}{A}}xright)-Cleft(y^{2}-{frac {E}{C}}yright)=-F}$

By completing the squares, the previous equation is rewritten as:

(7) ${displaystyle Aleft(x^{2}+{frac {D}{A}}x+{frac {D^{2}}{4A^{2}}}right)-Cleft(y^{2}-{frac {E}{C}}y+{frac {E^{2}}{4C^{2}}}right)={frac {D^{2}}{4A}}-{frac {E^{2}}{4C}}-F}$

Now convert the trinomials on the left into notable binomials:

(8) ${displaystyle Aleft(x+{frac {D}{2A}}right)^{2}-Cleft(y-{frac {E}{2C}}right)^{2}={frac {D^{2}}{4A}}-{frac {E^{2}}{4C}}-F}$

The term of the right to a constant called $t$ . According to the value of $t$ , the following cases are presented:

Yeah. $0}" xmlns="http://www.w3.org/1998/Math/MathML">t▪0{displaystyle tpur0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/29a2960e88369263fe3cfe00ccbfeb83daee212a" style="vertical-align: -0.338ex; width:5.101ex; height:2.176ex;"/>$ , the transverse and focal axles of the curve are parallel or colinear to the axis $x$ .
Yeah. $<math alttext="{displaystyle tt.0{displaystyle t vis0} <img alt="{displaystyle t$ , the transverse and focal axles of the curve are parallel or colinear to the axis $y$ .
Yeah. ${displaystyle t=0}$ the equation represents two straights that are cut.

Whatever the case, the center of the hyperbola or the intersection point of the two straights is always ${displaystyle Cleft(-{frac {D}{2A}},{frac {E}{2C}}right)}$ .

Equation of the hyperbola in its complex form

A hyperbola in the complex plane is the geometrical place formed by a set of points $z,$ on the plane ${displaystyle ReIm,}$ ; such that, any of them satisfies the geometric condition that the absolute value of the difference of their distances ${displaystyle |z-w_{1}|-|z-w_{2}|,}$ to two fixed points called foci ${displaystyle w_{1},}$ and ${displaystyle w_{2},}$ , is a positive constant equal to twice the distance (i.e. ${displaystyle 2l,}$ ) that exists between your center and any of your focal axis vertices:

{displaystyle |z-w_{1}|-|z-w_{2}|=2l,}

Evidently this operation is carried out on the set of complex numbers.

Equations in Polar Coordinates

Two hyperboles and their asymptotes in Cartesian coordinates.

Open right-to-left hyperbole:

{displaystyle r^{2}=asec 2theta ,}

Hyperbola open from top to bottom:

{displaystyle r^{2}=-asec 2theta ,}

Open hyperbola from northeast to southwest:

{displaystyle r^{2}=acsc 2theta ,}

Open hyperbola from northwest to southeast:

{displaystyle r^{2}=-acsc 2theta ,}

Hyperbola with origin at the right focus:

${displaystyle r(theta)={frac {a(varepsilon ^{2}-1)}{1-varepsilon cos theta }}}$

Hyperbola with origin at the left focus:

${displaystyle r(theta)={frac {a(varepsilon ^{2}-1)}{1+varepsilon cos theta }}}$

Parametric Equations

Open hyperbola from right to left:

{displaystyle {begin{matrix}x=asec t+h\y=btan t+k\end{matrix}};;tin ,]-pi /2,;pi /2[,cup ,]pi /2,;3pi /2[;;{mbox{(un intervalo para cada rama)}}}

${displaystyle {begin{matrix}x=pm asec t+h\y=btan t+k\end{matrix}};;tin ,]-pi /2,;pi /2[;{mbox{(un signo para cada rama)}}}$

More manageable is the parameterization

${displaystyle r(t)=(acosh(t),;pm bsinh(t)),;tin ,mathbb {R} }$ (a sign for each branch).

In this case the vertex in each branch is ${displaystyle r(0)}$ and points ${displaystyle r(t)}$ and ${displaystyle r(-t)}$ are symmetrical regarding the focal axis. In particular we can graph a part of each branch using any interval: ${displaystyle tin ,[-s,;s]}$ for example ${displaystyle tin ,[-1,;1]}$

Hyperbola open from top to bottom:

{displaystyle {begin{matrix}x=atan t+h\y=bsec t+k\end{matrix}}}

Also

${displaystyle r(t)=(asinh(t),;pm bcosh(t)),;tin ,mathbb {R} }$ .

In this case the vertex in each branch is ${displaystyle r(0)}$ and points ${displaystyle r(t)}$ and ${displaystyle r(-t)}$ are symmetrical regarding the focal axis.

In all formulas $h$ and $k$ are the abciss and ordered, respectively, of the center of the hyperbola, $a$ is the length of the larger seed, $b$ is the length of the minor semieje.

Focal parameters of the hyperbola y=1/x

Correspondence between the equilateral hyperbole

{displaystyle y=1/x}

and its focal shape

{displaystyle x'^{2}/2-y'^{2}/2=1}

To determine the focal parameters of an equilateral hyperbola defined by the equation:

{displaystyle y=1/x}

a matrix operation can be applied to modify the coordinates of a set of points of the plane when a spin is applied $theta$ :

{displaystyle {begin{bmatrix}x'\y'end{bmatrix}}={begin{bmatrix}cos theta &sin theta \-sin theta &cos theta end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}}

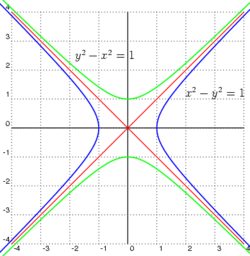
Like the horse hipster ${displaystyle y=1/x}$ is rotated with respect to the x-axis according to an angle ${displaystyle theta =45{text{°}}}$ , the transformation matrix takes the form:

{displaystyle {begin{bmatrix}x'\y'end{bmatrix}}={begin{bmatrix}{sqrt {2}}/2&{sqrt {2}}/2\-{sqrt {2}}/2&{sqrt {2}}/2end{bmatrix}}{begin{bmatrix}x\yend{bmatrix}}}

Starting from the equation of the equilateral hyperbola ${displaystyle y=1/x}$ The transformation becomes:

{displaystyle {begin{bmatrix}x'\y'end{bmatrix}}={begin{bmatrix}{sqrt {2}}/2&{sqrt {2}}/2\-{sqrt {2}}/2&{sqrt {2}}/2end{bmatrix}}{begin{bmatrix}x\1/xend{bmatrix}}}

Operating the matrix, it results:

{displaystyle x'={sqrt {2}}/2,(x+1/x)}

{displaystyle y'={sqrt {2}}/2,(-x+1/x)}

Calculating ${displaystyle x'^{2}-y'^{2}}$ You have to:

{displaystyle x'^{2}-y'^{2}=2/4,[(x^{2}+1/x^{2}+2)-(x^{2}+1/x^{2}-2)]=2}

from which it follows that:

{displaystyle x'^{2}/2-y'^{2}/2=1}

According to the focal notation, you have to have the horse hipérbola ${displaystyle y=1/x}$ has seeds of value ${displaystyle a=b={sqrt {2}}}$ , and the distance from their focus to origin is:

{displaystyle c={sqrt {a^{2}+b^{2}}}={sqrt {2+2}}=2}

Since the spotlights are in the symmetry line ${displaystyle y=x}$ (inclined 45°) that cuts the horse hipster ${displaystyle y=1/x}$ , its projected coordinates on the axes are:

{displaystyle f_{1}=2,({sqrt {2}}/2,{sqrt {2}}/2)=({sqrt {2}},{sqrt {2}})}

{displaystyle f_{2}=2,(-{sqrt {2}}/2,-{sqrt {2}}/2)=(-{sqrt {2}},-{sqrt {2}})}

Elements of the hyperbola

Obtaining a hyperbola through the section of a double cone.

Transversal or transverse axis

It is called the rectilinear segment where the focus and vertices of the hyperbola are found. Its value is ${displaystyle 2a}$ and is perpendicular to the conjugated axis.

Conjugate axis

It is the rectilinear segment that passes through the center of the hyperbola and which is perpendicular or normal to the transversal axis and whose length is ${displaystyle 2b}$ .

Focal axis

It is the rectilinear segment whose ends are the focus of the hyperbola and whose length is of ${displaystyle 2c}$ . This axis is colinear with the transversal axis.

Asymptotes

These are the lines that intersect at the center of the hyperbola and approach the branches as they move away from the center of the hyperbola. The equations of the asymptotes applicable to the equations (1) and (2) are, respectively:

${displaystyle left{{begin{array}{llr}y&=&displaystyle pm {frac {b}{a}}x\\y&=&displaystyle pm {frac {a}{b}}xend{array}}right.}$

The asymptotes of the hyperbolas represented by the equations (4) and (5 ) are expressed, respectively, by setting these equal to zero, as follows:

${displaystyle left{{begin{array}{lr}displaystyle left({frac {x-h}{a}}-{frac {y-k}{b}}right)left({frac {x-h}{a}}+{frac {y-k}{b}}right)=0\\displaystyle left({frac {y-k}{a}}-{frac {x-h}{b}}right)left({frac {y-k}{a}}+{frac {x-h}{b}}right)=0end{array}}right.}$

Vertices

The vertices of a hyperbola are the points that are the endpoints of its transverse axis.

Spotlights

It's two points, ${displaystyle F_{1},y,F_{2}}$ for which the difference of distances (at absolute value) remains constant at any point, $x$ Of such a hyperbola.

{displaystyle vert d(F_{1},x)-d(F_{2},x)vert =2a}

Center

Midpoint of the vertices and foci of the hyperbola.

Tangents

The tangent to a hyperbola at any point on the curve is bisector of the angle formed by the radii vectors of that point.

Radius of curvature

Sea ${displaystyle M(x_{0},y_{0})}$ a hipperbola point, then the curve radius is:

${displaystyle R=a^{2}b^{2}left({frac {x_{0}^{2}}{a^{4}}}+{frac {y_{0}^{2}}{b^{4}}}right)^{frac {3}{2}}={frac {(r_{1}cdot r_{2})^{1.5}}{ab}}}$

Areas

Area between a branch of a hyperbola and a chord that crosses it

Be a segment ${displaystyle AMN}$ where $A$ It's the vertex of a branch and $M$ and $N$ are the ends of a rope perpendicular to the focal axis, then the area is:

${displaystyle AMN=xcdot y-acdot bcdot ln left({frac {x}{a}}+{frac {y}{b}}right)=acdot bcdot cosh ^{-1}left({frac {x}{a}}right)}$

Area under an arc of hyperbola

Be a curved quadrilateral ${displaystyle OAMG}$ , formed by the points $O$ which is the origin of coordinates; $A$ that is a vertex; ${displaystyle M(x,y)}$ which is a point of the branch of a hyperbola and $G$ a point on an asymptote, such that the segment ${displaystyle MG}$ is parallel to the other asymptote. The area covered by the limits of the figure is:

${displaystyle OAMG={frac {acdot b}{4}}+{frac {acdot b}{2}}cdot ln left({frac {2OG}{c}}right)}$

Angular trisection

Angle Trisection (AOB) using an eccentric 2 (yellow curve)

As Apolonio de Perge demonstrated, a hyperbole can be used to trim an angle, a well studied geometry problem. Given an angle, you first draw a circle centered on your vertex Ointersecting the sides of the angle at the points A and B. Then the segment is drawn with the ends A and B and its perpendicular bisector $ell$ . Get yourself an eccentric hyperbole e=2 $ell$ as guideline and B as a focus. Sea P the intersection (superior) of the hyperbola with the circle. The angle POB triseca the angle AOB.

To test this, reflect the segment OP on the line $ell$ to get the point P like the image of P. The segment AP has the same length as the segment BP due to reflection, while the segment P has the same length as the segment BP due to the eccentricity of the hyperbola. Like OA, OP, OP and OB are all radios of the same circle (and therefore have the same length), the triangles OAP, OPP and OPB They're all congruent. Consequently, the angle has tripled, since 3×POB=AOB.

Other properties

Investment relationship between the hipérbola and the Bernouilli lemniscata

The investment of an equilateral hyperbola is a Bernouilli lemniscata and vice versa.
Bernouilli's lemniscata is the podiat of an equilateral hyperbola.

Contenido relacionado

Más resultados...