Huffman algorithm
The Huffman algorithm is an algorithm for the construction of Huffman codes, developed by David A. Huffman in 1952 and described in A Method for the Construction of Minimum-Redundancy Codes.
This algorithm takes an alphabet of n symbols, along with their associated occurrence frequencies, and produces a Huffman code for that alphabet and those frequencies.
Description
The algorithm consists of creating a binary tree that has each of the symbols per leaf, and built in such a way that following it from the root to each of its leaves, the Huffman code associated with it is obtained.
- Several trees are created, one by each of the symbols of the alphabet, consisting each of the trees in a node without children, and labeled each with its associated symbol and its frequency of appearance.
- They take the two trees less frequently, and unite creating a new tree. The root label will be the sum of the frequencies of the roots of the two trees that unite, and each of these trees will be a child of the new tree. The two branches of the new tree are also labeled: with a 0 left, and with a 1 right.
- Step 2 is repeated until there is only one tree left.
With this tree you can know the code associated with a symbol, as well as obtain the symbol associated with a given code.
To obtain the code associated with a symbol, proceed as follows:
- Start with an empty code
- Start the tree path on the leaf associated with the symbol
- Start a tree tour up
- Each time a level rises, add to the code the branch label that has been
- After reaching the root, reverse the code
- The result is the desired Huffman code
To obtain a symbol from a code, do it like this:
- Start the tree path at the root of the tree
- Remove the first symbol from the code to decode
- Descender for the branch tagged with that symbol
- Back to Step 2 until you reach a sheet, which will be the symbol associated with the code
In practice, the tree is almost always used to get all the codes at once; then they are saved to tables and the tree is dropped.
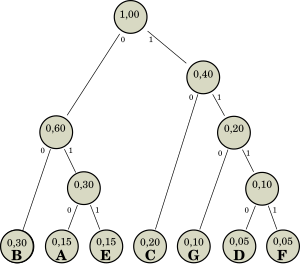
Example of use
The table describes the alphabet to be encoded, along with the frequencies of its symbols. The graph shows the tree built from this alphabet following the algorithm described.
| Symbol | Frequency |
|---|---|
| A | 0.15 |
| B | 0.30 |
| C | 0.20 |
| D | 0.05 |
| E | 0.15 |
| F | 0.05 |
| G | 0.10 |
It is easy to see what the code of the symbol E is: going up the tree we traverse branches labeled 1, 1 and 0; therefore, the code is 011. To obtain the code of D, we traverse the branches 0, 1, 1 and 1, so the code is 1110.
The inverse operation is also easy to perform: given the code 10 the branches 1 and 0 are traversed from the root, obtaining the symbol C. To decode 010, the branches 0, 1 and 0 are traversed, obtaining the symbol A.
Limitations
In order to use Huffman's algorithm, it is necessary to know in advance the frequencies of appearance of each symbol, and its efficiency depends on how close the estimated frequencies are to the real ones. Some implementations of Huffman's algorithm are adaptive, updating the frequencies of each symbol as it traverses the text.
The efficiency of the Huffman coding also depends on the balance that exists between the children of each node of the tree, being more efficient the lower the frequency difference between the two children of each node.
Examples:
- Binaria encoding is a particular case of Huffman encoding that occurs when all alphabet symbols have the same frequency. Therefore, binary encoding is the most efficient for any number of matchable symbols.
- The Huffman algorithm applied on an alphabet of two symbols will always assign 1 to the first and 0 to the second, regardless of the frequency of appearance of such symbols. In this case, no compression of the data is made, while other algorithms could get it.
One way to solve this problem is to group the symbols into words before running the algorithm. For example, if you have the string of length 64
AAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAAA
Huffman's algorithm applied only to symbols returns the code:
11111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111111
Also of length 64. However, if before using the algorithm, the symbols are grouped into the words "AA", "AB&# 34; and "B" (which are encoded as 1, 01, and 00), the algorithm returns the following string:
111111111111111111111111111111111
which has length 33, half that if it hadn't been clustered. If you look at the Huffman tree, you can see that the frequency difference between the branches of the tree is smaller than in the previous case.
Algorithm Variations
N-ary Huffman codes
It is possible to create ternary, quaternary, and, in general, n-ary Huffman codes. To do this, it is only necessary to make two modifications to the algorithm:
- Trees to create will have as many children as possible symbols can appear in Huffman codes. For example, if it is tender, trees will be created with three children; if it is quaternary, with four.
- If expressed as s the number of symbols in the alphabet to encode, and n the number of symbols appearing in the Huffman code, then s-1 must be multiple n-1. I mean, for a tender code, s must be worth 3, 5, 7, etc. If this condition is not met, then you must add "nulos" symbols often 0, which will serve only as a filling when building the tree.
Contenido relacionado
OSBOS
Sun SPARC
John carmack