Hexagon

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

A regular hexagon and its main angles

Irregular hexagon

In elementary plane geometry, a hexagon or hexagon (the latter version without "h" is deprecated, no longer collected in the DRAE) is a polygon with six sides and six vertices. Its name derives from the Greek ἑξάγωνον (from ἕξ, "six" and γωνία, "angle").

Properties

A hexagon has:

6 vertices and sides.
9 diagonals.
The sum of the internal angles of a hexagon is 720 degrees or $4pi$ radian.

Pairhexagon

Following the thread of a parallelogram, a parhexagon or parexagon is that particular hexagon, in which one side is equal and parallel to an opposite side, but each pair of these sides is of different size.

Proposition

Let ABCDEF be any irregular hexagon, join A with C; B with D; C with E; D with F; E with A; F with B. The six triangles ABC, BCD, CDE, DEF, EFA, FAB are formed. In each of them its center of gravity is located; which are denoted as A', B', C', D', E', F'. These points are successively joined, the hexagon A'B'C'D'E'F' is a parhexagon.

Regular hexagon

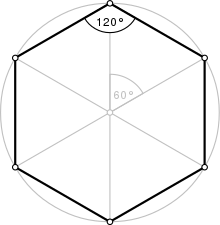
Measures of regular hexagon

The regular hexagon is a convex polygon with six equal sides and six equal angles, always divided into symmetric or asymmetric triangles.

The regular hexagon has the following properties:

Its internal angles are congruent by measuring 120° or $frac{2pi}{3}$ rad. Outcome $A_i = frac{180(6-2)}{6}$
Each external angle of the regular hexagon measures 60° or $frac{pi}{3}$ rad.
It is intimately related to equilateral triangles:
- By uniting each vertex with its opposite, the regular hexagon is divided into six equilateral triangles.
- Numerize the vertices from 1 to 6 in the time sense. By joining the odd vertices you get an equilateral triangle; by joining the pair vertices you get another one.
In addition to squares and equilateral triangles, the regular congruent hexagons (or equals) are the regular polygon third parties that can be assembled to fully coat a flat surface without leaving any vain.
The six sixth roots of 1 or the complex numbers that solve the equation $z^6 -1 = 0$ are on the vertices of a regular hexagon located in the complex plane, being the first vertex point (1.0).

A regular hexagon is inscriptible and circumscribable in a circumference.According to the figure, ${displaystyle r_{i}}$ would be the radius of the registered circle, ${displaystyle r_{u}}$ circle radius and $a$ the length on one side. Equalities are:

{displaystyle a=r_{u}}

, the length of one side is equal to the radius of the circle circumscribed.

{displaystyle r_{i}=cos(30^{circ })r_{u}}

In this way the radios of the circumferences are related, then:

{displaystyle r_{i}={frac {sqrt {3}}{2}}r_{u}}

and we can conclude that

{displaystyle a=r_{i}={frac {r_{u}}{2}}{sqrt {3}}}

For a regular Circle Hexagon and side length

{displaystyle r_{u}=a=1}

the radius of the inscribed would be approximately

{displaystyle r_{i}approx 0.866}

The perpendiculars traced by the average points of the regular hexagon and the bisectrices of the internal angles of the regular hexagon are axes of symmetry of the same.

Perimeter

Its perimeter is six times the length of its side.

P = ncdot l_n = 6 l_6

where n is the number of sides and

l_n

The length of the side.

The perimeter according to the apothesis ( ${displaystyle a_{p}}$ It is

{displaystyle P=4cdot a_{p}cdot {sqrt {3}}}

And depending on the circle radius ( ${displaystyle r_{u}}$ It is

{displaystyle P=6cdot r_{u}}

Area

Area of regular hexagon

If the length of the apothem a₆ of the polygon is known, an alternative to calculate the area is:

A = frac{Pcdot a_p}{2} = frac{6l_6cdot a_p}{2} = 3l_6 cdot a_p

A = 2sqrt{3}cdot a_p^2

If we only know the side l₆ we can calculate the area with the following formula:

A = l_6^2 frac{3sqrt{3}}{2}

, which equals the areas of six equilateral triangles that are obtained by joining the center with the six vertices.

Geometric construction

Geometric construction of a regular hexagon.

A regular hexagon can be constructed using only a straightedge and compass:

Given a point O any, to draw a circle whose radius is equal to the side of the hexagon to build;
Choose a point A on the circumference and draw a diameter that crosses O and A. Mark the other point where this diameter intersects the circumference as D;
Supporting the compass at the point A, trace an arch that crosses O, cutting the circumference at two points, marked as B and F;
Supporting the compass at the point D, trace an arch that crosses O, cutting the circumference at two points, marked as C and E

Gallery of natural and artificial hexagons

The continental France or metropolitan part of France receives the name of Hexagon (l'Hexagone in French), for having a vaguely hexagonal form.
The shell shields of a turtle are made up of hexagons.
At the north pole of Saturn is a pattern of clouds forming a hexagon.
The hexagonal chess of Władysław Gliński.
The Chinese-style pavilions in the botanical gardens have a hexagonal structure.
Hexagonal is a hexagonal-type architecture theatre located in Reading, UK.
Hexagonal barn.
Aerial view of Tortugas Secas National Park.
Hexagonal window of a house.
An image of ordered bubbles one to the other gives the illusion of seeing hexagons.
The hanksita, of one of the many minerals of the hexagonal crystal system
Panals are built with hexagonal forms.
$Columnas de basalto formadas naturalmente de la Calzada del Gigante en Irlanda del Norte; las masas grandes deben enfriarse lentamente para formar un patrón de fractura poligonal.$
Baseline columns formed naturally from the Giant Calzada in Northern Ireland; the large masses should slowly cool down to form a pattern of polygonal fracture.
The micrograph of a snowflake.
The crystalline structure of the Grapheno is formed by a grid of hexagons.
The benzene is an aromatic compound with hexagonal shape.
Crystalline structure of a molecular hexagonal hexagonal hexagonal ring.
E-ELT mirror segments assembled.
The mirror of the James Webb space telescope is composed of 18 hexagonal segments.

Contenido relacionado

Más resultados...