Heat conduction
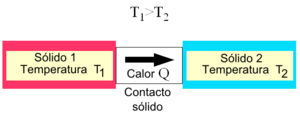
The conduction of heat or transfer of energy in the form of heat by conduction is a process of heat transfer based on direct contact between bodies, without exchange of matter, because heat flows from a body of higher temperature to another of lower temperature that is in contact with it. The physical property of materials that determines their ability to conduct heat is thermal conductivity. The inverse property of thermal conductivity is thermal resistivity, which is the ability of materials to oppose the passage of heat.
The transmission of heat by conduction, between two bodies or between different parts of a body, is the exchange of internal energy, which is a combination of the kinetic energy and potential energy of its microscopic particles: molecules, atoms and electrons. The thermal conductivity of matter depends on its microscopic structure: in a fluid it is mainly due to random collisions of molecules; in a solid it depends on the exchange of free electrons (mainly in metals) or the modes of vibration of its microscopic particles (dominant in non-metallic materials).
For the simplified case of steady heat flow in only one direction, the heat transmitted is proportional to the area perpendicular to the heat flow, to the conductivity of the material, and to the temperature difference, and is inversely proportional to the thickness:
| Symbol | Name |
|---|---|
| QΔ Δ t{displaystyle {frac {Q}{Delta t}}} | Heat transmitted by time unit |
| k{displaystyle k} | Thermal conductivity |
| A{displaystyle A} | Area of contact surface |
| x{displaystyle x} | Material thickness |
| (T1− − T2){displaystyle (T_{1}-T_{2})} | Temperature difference between hot focus and cold |
Heat transfer processes
Heat is transferred by one of the following processes:
- Driving: heat transmission by contact without material transfer.
- Convection: heat transmission by the transfer of the same heat carrier matter.
- Radiation: transmission of energy through the emission of electromagnetic waves or photons.
The transfer of thermal energy or heat between two different by conduction or convection requires the direct contact of the molecules of different bodies, and they differ in that in the first there is no macroscopic movement of matter while in the second there is. For ordinary matter conduction and convection are the main mechanisms in "cold matter", since the transfer of thermal energy by radiation only represents a minuscule part of the energy transferred. The transfer of energy by radiation increases with the fourth power of the temperature (T4), being only a significant part from temperatures above several thousand kelvins.
It is the way of transmitting heat in solid bodies; a body is heated, the molecules that directly receive the heat increase their vibration and collide with those that surround them; these in turn do the same with their neighbors until all the molecules in the body are agitated. For this reason, if the end of a metal rod is heated with a flame, it takes some time for the heat to reach the other end. Heat is not transmitted equally easily by all bodies. There are so-called "good conductors of heat", which are those materials that allow heat to pass through them. The "bad conductors or insulators" They are the ones that oppose a lot of resistance to the passage of heat.
It should be noted that when heat transmission occurs between two bodies, the three enunciated forms of heat generally coexist, what happens is that one of them prevails over the others.
A practical example occurs when turning on an electric lamp where it can be verified that:
The lamp holder gets hot because there is heat transfer by conduction.
The air surrounding the lamp is heated and rises by convective heat transmission.
As we bring our hand closer to the lit lamp, we notice the emission of heat by radiation.
Fourier's Law
Thermal conduction is determined by Fourier's law, which states that the flow of heat transfer by conduction in an isotropic medium is proportional and in the opposite direction to the temperature gradient in that direction. Consider a plate of solid material of surface A, sandwiched between two large plates separated by a distance Y. Assume that for t < 0 the material is at a temperature To. At time t=0, a plate is suddenly heated to temperature Ts and remains constant. As time elapses, the temperature profile changes with respect to position until, after this transition period, the temperature profile linear (steady state) with time and independent of position is reached. Once this has occurred, to maintain temperatures there must be a constant heat flow, and for low temperature gradients the following is true, differentially and applied to the three dimensions (rectangular coordinates):
| Symbol | Name | Unit |
|---|---|---|
| q{displaystyle mathbf {q} } | Heat flow vector per surface unit | W m-2 |
| k{displaystyle k} | Thermal conductivity (constant proportionality) | W m-1 K-1 |
| ► ► T{displaystyle {nabla }T} | Gradient of the temperature field inside the material | K-1 |
It is concluded that in an isotropic medium, heat flows by conduction in the direction in which the temperature drop is more pronounced. For a moving fluid, Q represents the heat energy flux density relative to the moving fluid. In an integral way, the heat that passes through a surface S per unit of time is given by the expression:
dQSdt=∫ ∫ Sq⋅ ⋅ dS=− − k∫ ∫ S► ► T⋅ ⋅ dS{displaystyle qquad {frac {dQ_{S}}{dt}}}=int _{S}mathbf {q} cdot dmathbf {S} =-kint _{S}nabla Tcdot dmathbf {S} }
The more general case of the conduction equation, expressed in differential form, reflects the balance between the net heat flux, the heat generated, and the heat stored in the material.
| Symbol | Name |
|---|---|
| α α {displaystyle alpha } | Thermal dysfunction |
| ▪ ▪ 2T▪ ▪ x2+▪ ▪ 2T▪ ▪ and2+▪ ▪ 2T▪ ▪ z2≡ ≡ ► ► 2T{displaystyle {frac {partial ^{2}T}{partial x^{2}}}}}+{frac {partial ^{2}T}{partial y^{2}}}}}{frac {partial ^{2}T{partial z^{2}}}}}{equiv nabla ^{2}{ | Laplatian temperature field operator, measuring the net heat flow |
| ρ ρ {displaystyle rho } | Density of material |
| Cp{displaystyle C_{p}} | Specific heat of the material |
| q! ! G{displaystyle {dot {q}}_{G}}} | Heat generated by volume unit |
| ▪ ▪ T▪ ▪ t{displaystyle {frac {partial T}{partial t}}}} | Temperature variation with time |
where:
| Symbol | Name |
|---|---|
| α α {displaystyle alpha } | Thermal dysfunction |
| k{displaystyle k} | |
| ρ ρ {displaystyle rho } | Density of material |
| Cp{displaystyle C_{p}} | Specific heat of the material |
The conduction equation, which is a particular case of Poisson's equation, is obtained by applying the principle of conservation of energy.
Thermal conductivity
Thermal conductivity is an intrinsic property of materials that assesses the ability to conduct heat through them. The value of conductivity varies depending on the temperature at which the substance is found, which is why measurements are usually made at 300 K in order to be able to compare some elements with others.
It is high in metals and in general in continuous bodies, and it is low in gases (despite the fact that in them the transfer can be done through free electrons) and in ionic and covalent materials, being very low in some materials special materials such as fiberglass, which are therefore called thermal insulators. For thermal conduction to exist, a substance is needed, hence it is null in the ideal vacuum, and very low in environments where a high vacuum has been practiced.
In some industrial processes, work is being done to increase heat conduction, either by using highly conductive materials or configurations with a high contact area. In others, the effect sought is just the opposite, and it is desired to minimize the effect of conduction, for which low thermal conductivity materials, intermediate voids, and configurations with little contact area are used.
| Material | λ | Material | λ | Material | λ |
|---|---|---|---|---|---|
| Steel | 47-58 | Corcho | 0.04-0.30 | Mercury | 83.7 |
| Water | 0,58 | Tiny | 64.0 | Mica | 0.35 |
| Air | 0.02 | Glass fiber | 0.03-0,07 | Nickel | 52.3 |
| Alcohol | 0.16 | Glicerina | 0.29 | Gold | 308,2 |
| Alpaca | 29.1 | Iron | 80.2 | Paraffin | 0.21 |
| Aluminium | 209,3 | Brick | 0.80 | Silver | 406,1-418,7 |
| Asbestos | 0.04 | Refractory brick | 0.47-1.05 | Plomo | 35,0 |
| Bronze | 116-186 | Brass | 81-116 | Vidrio | 0.6-1.0 |
| Zinc | 106-140 | Lithium | 301,2 | Yes | 0.488 |
| Copper | 372,1-385,2 | Wood | 0.13 | Polyethylene | 0.035 |
The coefficient of thermal conductivity (λ) expresses the quantity or flow of heat that passes through the unit area of a sample of the material, of infinite extension, plane-parallel faces and unit thickness, when a distance is established between its faces. temperature difference equal to unity, under steady-state conditions.
In the SI system, thermal conductivity is expressed in units of W⋅m-1⋅K-1 (J/s⋅m-1⋅°C-1). It can also be expressed in units of British thermal units per hour per foot per degree Fahrenheit ( Btu⋅h-1⋅ft-1⋅°F-1). These units can be converted to W/(m K) using the following conversion factor: 1 Btu/(h ft °F) = 1.731 W/(m K).
Contenido relacionado
Piezoelectricity
Wilhelm roentgen
Gluon