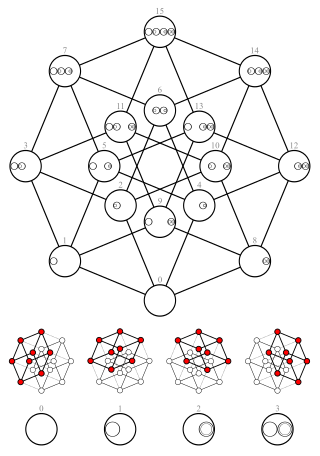
Hasse diagram

P(P(P({})) elements))) in Hasse diagram.

In mathematics, a Hasse diagram is a simplified graphical representation of a finite partially ordered set. This is achieved by removing redundant information. To do this, an ascending edge is drawn between two elements only if one follows the other without other intermediate elements. The diagram is named in honor of the German mathematician Helmut Hasse.

In a Hasse diagram the need to represent:

• cycles of an element, since it is understood that a partial order relationship is reflective.
• arists that deduce from the transitivity of the relationship.

Definition

• Two members x e and of a partially ordered set S «and follow x» yes x ≤ and and there is no element of S between x e and.

The partial order is then precisely the transitive closure of the relation to follow.

• Hasse diagram S is defined as the set of all pairs ordered (x, and) such that and follow a x, that is, the Hasse diagram can be identified with the relationship.

Example

Specifically, one represents each member of S as a black dot on the page and draws a line going up from x to y if y follows x.

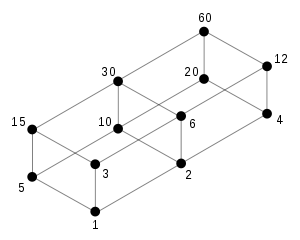
For example, let the set A = {1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30, 60} (all divisors of 60). This set is partially ordered by the divisibility relation. Its Hasse diagram can be represented as follows:

For example, in the Hasse diagram of the poset of all divisors of a number n, partially ordered by divisibility, n itself is at the top of the diagram, the number 1 would be at the bottom, and the smaller divisors (primes) would follow the bottom element.

Relationship with graphs

A Hasse diagram can also be seen as a graph from which all loops and edges are removed which can be deduced with the transitive property and the reflexive property.

The difficulty of finding a good Hasse diagram

Follow-to relationships are uniquely defined from the initial order relationship. This makes the edges of the Hasse diagram and the connecting points uniquely determined as well. But there is an additional problem: finding a suitable location for the vertices that can reflect some of the underlying symmetries. In this sense, finding a good diagram is difficult.

Several algorithms for drawing "good" diagrams have been proposed, but today their construction still relies on strong human intervention. In fact, even a human needs quite a bit of practice to craft them.

The following examples correspond to Hasse diagrams of the same order relation: