Gravitational field

In physics, the gravitational field or gravitational field is a field of forces that represents gravity. If a mass is available in a certain region of space ${displaystyle M}$, space around ${displaystyle M}$ acquires certain characteristics that it did not have when it was not ${displaystyle M}$. This fact can be verified approaching another mass ${displaystyle m}$ and finding that the interaction occurs. To the physical situation of the mass ${displaystyle M}$ is called the gravitational field. Affirm that there is something around ${displaystyle M}$ is purely speculative, since only the field is noticed when the other mass is placed ${displaystyle m}$The one called mass witness or test mass.

The treatment received by the gravitational field is different depending on the needs of the problem:

• In Newtonian physics or classic physics the gravitational field is represented by a vector field.
• In relativistic physics, the gravitational field is represented by a tensorial field of second order marcea.

Gravitational field in classical physics

We can associate to each point of space the vector intensity of the gravitational field created by the presence of a mass M. The set of all these vectors at the different points of space is a Gravitational Field.

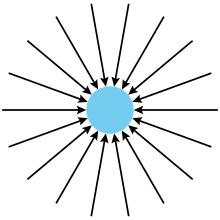
In Newtonian physics, the gravitational field is represented by a conservative vector field whose field lines are open. It can be defined as the force per unit mass that a point particle will experience in the presence of a mass distribution. Its dimensions are, therefore, those of an acceleration, although the dimension of force per unit of mass is usually used -which is equivalent- and its intensity is expressed in N/kg (newtons/kilogram).

Mathematically, the intensity ${displaystyle g}$ of the gravitational field produced by any mass distribution is defined as:

${displaystyle g={underset {mto 0}{mathop {lim} },{frac {F}{m}}}}}{mathop {lim } } },{frac {F}{F}{m}}}}}}$

where:

• ${displaystyle m}$ is a test mass
• ${displaystyle F}$ is the gravitational force that acts on the test mass

Gravitational fields are additive. The intensity of the gravitational field created by a mass distribution is equal to the vectorial sum of the intensities of the fields created by its different constituent elements.

Gravitational Fields

The field ${displaystyle mathbf {g} }$ created by a punctual mass ${displaystyle M}$ or a homogeneous mass sphere ${displaystyle M}$ in an outer point to the sphere is directed towards its center and is given by the expression:

(1)${displaystyle mathbf {g} =-{frac {GM}{{{{{r}}}}}}{frac {mathbf {r}}}{r}}}}}}{frac {GM}{{{{{{r}}}}}{{{{{mathbf {u}}} }_{r}}}}}}}}$

where ${displaystyle r}$ is the distance from the point to the center of the sphere. This equation (1), by which the field decrees according to the law of the reverse of the square is only valid external points to the sphere.

Calculation of the gravitational field created by a continuous distribution of matter.

Within the sphere it can be shown that the field varies according to a law dependent on the distribution of mass; thus, for the case of a homogeneous sphere of radio ${displaystyle R}$, grows linearly from zero in the center of the sphere to its surface, where it is worth:

(2)${displaystyle g=-{frac {GM}{{{R}^{2}}}}}}$

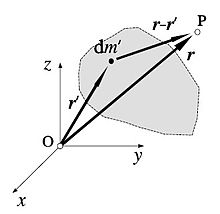
The field ${displaystyle mathbf {g} }$ created by a totally general mass distribution at a space point ${displaystyle mathbf {r} }$ is determined by integration, adding vectorially the contributions of infinitesimal mass portions:

(3)${cHFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cH00FFFF}{cHFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFF}{cHFFFFFF}{cHFFFF}{cHFFFFFFFF}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cH}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{cHFFFFFFFFFFFFFFFFFFFF}{cHFFFFFFFFFFFFFFFF}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFF}{cH00}{cH00}{cH}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF$

The interest of describing gravitational interaction through a field lies in the possibility of expressing gravitational interaction as the product of two terms, one that depends on the local value of the field ${displaystyle mathbf {g} }$ and another a climbing property that represents the answer of the object that suffers the action of the field. For example, the movement of a planet can be described as the orbital movement of the planet in the presence of a gravitational field created by the Sun.

The divergence and the curl of the gravitational field are worth:

${displaystyle nabla cdot mathbf {g} =-4pi Grho quad quad nabla times mathbf {g} =0}$

The first indicates that its sources or origins are scalar (mass) and the second indicates that it is conservative.

Gravitational Potential

Circulation between two points of a central force field. The result does not depend on the path followed, but only on the positions of the two points. Consequently, the central force field is conservative.

We can demonstrate that the gravitational field is conservative simply by checking that its circulation between two generic points A and B is independent of the path or trajectory that we follow. Indeed, calculating said circulation (work per unit of mass), and in accordance with the notation reflected in the figure, we obtain:

$♪♪$

That is, the work (circulation) performed by the field is a function solely of the values that a certain scalar function of a point takes on at the ends of the trajectory, regardless of the path followed. This scalar function is called gravitational potential and, in the case of the field created by a point mass (or a spherical mass distribution) it is expressed by:

${displaystyle phi (r)=-{frac {GM}{r}}}}}$

In this way,

${displaystyle {frac {{W}_{AB}}{m}}=left({frac {GM}{{{{{r}_{B}}}}}-{frac {GM}{{{{{r}_{A}}}}}{right)=-left(phi ({{{{r}_{B}}})})})}$

where the negative sign indicates that the work done by the gravitational force represents a decrease in the gravitational potential. That is, if the particle moves in the direction of the field, the work that the field does on it is positive and its gravitational potential decreases.

So at every point of space you can assign a gravitational potential ${displaystyle phi }$ related to the density of the distribution of mass mediate its laplatian and the gravitational field by its gradient by:

${displaystyle {{nabla }^{2}phi }=Delta phi =4pi rho quad nabla phi =-mathbf {g} } }$

Field lines

A line of force or field line, usually in the context of electromagnetism, is the curve whose tangent gives the direction of the field at that point. As a result, it is also perpendicular to the equipotential lines in the conventional direction from high to low potential. They are a useful way of graphically depicting a field, although they are imaginary and have no physical presence.

Gravitational field in relativistic physics

In the theory of general relativity, the gravitational field is not described as a field of forces, but rather the curved paths that bodies follow in three-dimensional space are just a reflection that space-time is curved. According to the theory of general relativity, a point particle in free fall in a gravitational field is following a line of least curvature, called a geodesic, on a curved space-time. Therefore, the curvature of three-dimensional trajectories is due to the fact that the straightest possible line in four-dimensional space-time does not project as a line, seen from three-dimensional space.

The gravitational field is interpreted in relativity as the curvature of space-time that, in the presence of matter, ceases to be flat. Where space-time is not flat, this fact is perceived as a local gravitational field, and vice versa, where a gravitational field is perceived, there is a curved geometry of space-time. Thus, Einstein's relativistic theory of the gravitational field is a theory of the local geometric structure of space-time. In this theory, the Ricci curvature tensor is associated with the energy-momentum tensor of matter:

${displaystyle R_{ik}-{1 over 2}g_{ik}R={8pi G over c^{4}T_{ik}}}$

Where:

${displaystyle R_{ik},}$ are the components of the Ricci curvature tensor.

${displaystyle g_{ik},}$ are the components of the metric tensor that allows measuring distances in the curved space-time.

${displaystyle R,}$ It's Ricci's curvature climber.

${displaystyle T_{ik},}$ are the components of the energy-impulse tensor of the matter that creates the field.

${displaystyle G,c,}$ are the constant of universal gravitation and the speed of light.

Weak field approximation

For weak gravitational fields, giving rise to asymptotically flat spacetime and bodies moving in it at velocities small compared to the speed of light (from the point of view of stationary observers far away from the gravitational source), The geometry of curved space-time can be represented by a metric very close to the Euclidean metric given by:

${displaystyle mathrm {d} s^{2}=-left(c^{2}+2phi _{gright)mathrm {d} t^{2}+mathrm {d} x^{2}+mathrm {d} and{2} +mathrm {d} z^{2}$

The equations of motion of a particle in a weak gravitational field of the above type are given by:

${cHFFFFFF}{cHFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFF}{cHFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFF}{cHFFFF}{cHFF}{cHFFFF}{cHFFFF}{cHFF}{cHFFFFFF}{cHFF}{cH}{cH}{cHFFFFFFFF}{cHFFFF}{cHFFFFFFFFFFFF}{cHFF}{cHFF}{cHFFFFFF}{cHFF}{cHFFFFFF}{cH}{cHFF}{cHFFFFFF}{cHFF}{cHFF}{cH00}{cHFFFFFFFFFFFF}{cHFFFF}{cHFF}{cH}{cH$

The first of the above implies that space coordinates vary similarly to the classic case, although affected by a temporary slowing factor ${displaystyle ({dot {t}}{2}}}}$, while the relationship between the time itself and the time coordinate is obtained by integrating the second equation:

${displaystyle t(tau)=C_{2}+int _{0}^{tau }C_{1exp left(-int _{0}{tau _{2}{frac}{2}{2{dot {mathbf {r}}}{cdot {b }{b }{b }{b }{b }{b }}{b }}{c }{b }{c }{c }{c }{c }{c }{c }{c }{c }}{c }{c }{c }{c }{c }{$

Stationary space-time

In the general case of a non-stationary space-time it is not possible to approximate the field by means of a field of forces derived from a potential. However, in the case of a static space-time it is possible to find an analogue to the gravitational potential, which in the weak field limit reduces to the Newtonian potential. To see this, we start from the general form of the metric in a static space-time that is given by:

${displaystyle mathrm {d} s^{2}=-lambda (x^{1},x^{2},x^{3})mathrm {d} totimes mathrm {d} t+mathrm {d} sigma ^{2}(x^{1},x^{2},x^{3}{3}}}}}$

From the fundamental relationship for energy-momentum, we have that:

${displaystyle g_{alpha beta }P^{alpha }P^{beta }=-lambda {frac {E^{2}{c}{c^{2}}}}{c^{2}=-m^{2}c^{2}{2}}}$

you can define an "effective gravitational potential" ${displaystyle phi _{g}}$ such that:

${displaystyle 1+{frac {2phi _{g}}{c^{2}}{lambda}$

From the last two equations we have that:

${displaystyle E={frac {1}{sqrt {1+(2phi _{g}/c^{2}}}}}{sqrt {p^{2}c^{2}{2}{2}{2}}{2⁄2}}{4}{frac{2}{2}{1⁄2}{1⁄2}{1⁄2⁄2}{2}{1⁄2}}}{1⁄2}{1⁄2}{c}{c}}{1⁄2}{1⁄2}{1⁄2}{1⁄2}}{1⁄2}{1⁄2}{1⁄2}}{1⁄2}{1⁄2}{1⁄2}{1⁄2}}}}}{1⁄2}{1⁄2}{1⁄2}{1⁄2}}{c}{1⁄2}{1⁄2}{1⁄2}}}{c}{c}{c}{c}}{c}{$

For weak fields, this last equation can be rewrite, using the approach that ${displaystyle {sqrt {1+x}approx 1+x/2}$like:

${displaystyle Eapprox left(1-{frac {phi _{g}{c^{2}}}{2}{2}{2}left(1+{frac {1}{2}{2}{frac}{2}{p^{2}}{mc^{2}}{2}{2}{x1⁄2}{x1⁄2}{x1⁄2}{2}{2}}{x1⁄2}}}}{x1⁄2}{x1⁄2}}{x1⁄2}}{x1⁄2}}}{f}}{x1⁄2}$

which coincides with the classical expression of Newtonian mechanical energy plus rest mass. If this approximation is not used, the effective potential energy for a static space-time can be written as:

${displaystyle E={frac {1}{sqrt {1+(2phi _{g/}c^{2}}}}}}}}{sqrt {p^{2}c^{2}{2}}{2}}{4}{4}{4}}{approx (1-phi _{g}/c^{2}{2}{2}{x}{2}{x {p}{2}{2}{2}{2}{x}{2}{2}{2}{x1⁄2}{2}{2}{2}{2}{2}{2}{cccccc}{cccccccccccccccccccccccccccccccccccccccc$

For the slightly more general case of a stationary spacetime the two Hansen potentials can be used, one of which plays a role analogous to the Newtonian potential and the other gives the gravitomagnetic effect.

General space-time

If spacetime is not stationary, there is no local analogue of gravitational energy. In fact, in the most general case in general relativity an energy-momentum tensor cannot be defined for the gravitational field, so the notion of conservation of energy in the general case is not analogous to the classical case. Although there is a local law of conservation of energy, there is no global magnitude that can be considered the energy of the system, including the gravitational field.