Graphic Schema Theory

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Them graphs are the object of study of this branch of mathematics. Up the fish graph, in the middle the bow graph and down the dodecaedro graph.

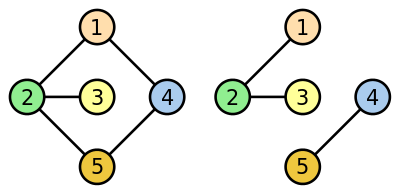
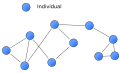
La Graph theoryAlso called Graphics theory, it is a branch of mathematics and computer science that studies the properties of graphs. Graphs should not be confused with the graphics, which is a very wide term. Formally, a graph ${displaystyle G=(V,E)}$ is an orderly couple in which $V$ is a non-empty set of vertices and $E$ It's a set of edges. Where $E$ consists of unordered pairs of vertices, such as ${displaystyle left{x,yright}in E}$ So it's said that $x$ e $y$ are adjoining; and in the graph is represented by a non-orientated line that such vertices. If the graph is directed it is called digit, it denotes $D$ And then the pair $(x,y)$ is an orderly pair, this is represented with an arrow that goes from $x$ a $y$ and it is said that $(x,y)in E$ .

Graph theory has its foundations in discrete mathematics and applied mathematics. This theory requires different concepts from various areas such as combinatorics, algebra, probability, polygon geometry, arithmetic, and topology. Currently he has had the greatest influence in the field of information technology, computer science and telecommunications. Due to the large number of applications in the optimization of routes, processes, flows, search algorithms, among others, a whole new theory was generated, known as network analysis.

History

The 7 Pregel River bridges in Königsberg.

The origin of graph theory dates back to the 18th century with the problem of Königsberg bridges, which consisted of finding a path that crossed the seven bridges of the Pregel River (54°42′12″N 20°30′56″E / 54.70333, 20.51556) in the city of Königsberg, currently Kaliningrad, so that all the bridges were covered, passing through each of them only once. Leonhard Euler's work on the problem entitled Solutio problematis ad geometriam situs pertinentis (The solution of a problem relative to the geometry of position) in 1736, is considered the first result of graph theory. It is also considered one of the first topological results in geometry (which does not depend on any measurement). This example illustrates the deep relationship between graph theory and topology.

Then, in 1847, Gustav Kirchhoff used graph theory for the analysis of electrical networks by publishing his circuit laws to calculate voltage and current in electrical circuits, known as Kirchhoff's laws, considered the first application of graph theory to an engineering problem.

In 1852, Francis Guthrie posed the four-color problem, which states that it is possible, using only four colors, to color any map of countries in such a way that two neighboring countries never have the same color. This problem, which was not solved until a century later by Kenneth Appel and Wolfgang Haken in 1976, can be considered as the birth of graph theory. In trying to figure it out, mathematicians defined fundamental graph-theoretical terms and concepts.

In 1857, Arthur Cayley studied and solved the problem of enumeration of isomers, chemical compounds with the same composition (formula) but different molecular structures. For this he represented each compound, in this case saturated hydrocarbons C _n H _{2n + 2}, by means of a tree graph where the vertices represent atoms and the edges the existence of chemical bonds..

The term “graph” comes from the English expression graphic notation, first used by Edward Frankland and later adopted by Alexander Crum Brown in 1884 and which made reference to the graphical representation of the bonds between the atoms of a molecule.

The first book on graph theory was written by Dénes Kőnig and published in 1936.

In the late 1940s and early 1950s, along with the first formal studies of cliques in sociomatrixes and of centrality in sociograms, graph theory was introduced as a key tool for the sociometry and social network analysis.

Composition of a graph

Arists: These are the lines that link the vertices of a graph.
- Adjacent archers: Two edges are adjacent if they converge on the same vertex.
- Parallel players: Two edges are parallel if the initial and final vertices are the same vertice
- Cyclical players: Arists who leave a vertex to enter it.
- Cruce: Point where two edges cross.

Vetices: Vertices are the elements that form a graph. Each bears a characteristic valence according to the situation, which corresponds to the number of edges that converge in the vertice.

Camino: It is called road to a set of vertices interconnected by edges. Two vertices are connected if there is a way between them.

Types of graphs

Simple graph: Or just graph is the one who accepts a single edge by joining any two vertices. This is equivalent to saying that any arist is the only one that links two specific vertices. It's the standard definition of a graph.
Multigraph or pseudograph: He accepts more than one edge between two vertices. These edges are called multiple or bonds (loops in English). Them simple graphs are a subclass of this category of graphs. Also called General graphs.
oriented graph: directed graph or digit. They are graphs in which one has been added guidance a las aristas, represented graphically by an arrow.
Graph tagged: Graphs in which a weight to the edges (generally whole number) or tagged to the vertices.
Random rate: Graph whose edges are associated with a probability.
Hypergraph: Graphs in which the edges have more than two ends, that is, the edges are incidents to 3 or more vertices.
Infinite Graph: Graphs with set of vertices and edges of infinite cardinal.
Flat tap: The flat graphs are those whose vertices and edges can be represented without any intersection between them. We can establish that a graph is flat thanks to the Kuratowski Theorem.
Regular Graph: A graph is regular when all your vertices have the same degree of valence.
Dual Graph: The dual graph $G'$ of a graph $G$ (plane) is the one who has a vertex for each region of $G$ , and an edge for every edge in $G$ joining two neighboring regions.

Graph Representation

Main article: Graph (data structure)

There are different ways to represent a (simple) graph, besides the geometric and many methods to store them in a computer. The data structure used depends on the characteristics of the graph and the algorithm used to manipulate it. Among the simplest and most used structures are lists and matrices, although a combination of both is frequently used. Lists are preferred in sparse graphs because they are efficient in memory usage. On the other hand, arrays provide fast access, but can consume large amounts of memory.

List structure

Incidence list - The edges are represented with a pair vector (ordered, if the graph is directed), where each pair represents one of the edges.

Adjacency list - Each vertex has a list of vertices which are adjacent to it. This causes redundancy in an undirected graph (as A exists on the B adjacence list and vice versa), but searches are faster, at the extra storage cost.

Grade list - Also called sequence of degrees or Graphical succession of a non-directed graph is a sequence of numbers, which corresponds to the degrees of the graph vertices.

Matrix Structures

Adjacent matrix - The graph is represented by a square M matrix $n^{2}$ Where $n$ It's the number of vertices. If there's an edge between a vertex $x$ and a vertex $y$ , then the element ${displaystyle m_{x,y}}$ That's it. $1$ Otherwise it is ${displaystyle 0}$ .

Incidence matrix - The graph is represented by a matrix $A$ (arists) by $V$ (vertices), where [vertice, arista] contains the information of the arist ( $1$ means connected and ${displaystyle 0}$ not connected).

Grafo

{displaystyle G=(V,A)}

Sets

Adjacent matrix

Incidence matrix

Sequence of degrees

Adjacency list

{displaystyle {begin{aligned}V={&1,2,3,4,5,6}\A={&{1,1},{1,2},{1,5},{2,3},\&{2,5},{3,4},{4,5},{4,6}}end{aligned}}}

{displaystyle {begin{pmatrix}1&1&0&0&1&0\1&0&1&0&1&0\0&1&0&1&0&0\0&0&1&0&1&1\1&1&0&1&0&0\0&0&0&1&0&0\end{pmatrix}}}

{displaystyle {begin{pmatrix}1&1&1&0&0&0&0&0\0&1&0&1&1&0&0&0\0&0&0&1&0&1&0&0\0&0&0&0&0&1&1&1\0&0&1&0&1&0&1&0\0&0&0&0&0&0&0&1\end{pmatrix}}}

{displaystyle (3,3,2,3,3,1)}


vertex	Adjacency list
$1$	${displaystyle 1,2,5}$
$2$	${displaystyle 1,3,5}$
${displaystyle 3}$	${displaystyle 2,4}$
${displaystyle 4}$	${displaystyle 3,5,6}$
$5$	${displaystyle 1,2,4}$
${displaystyle 6}$	${displaystyle 4}$

Graph Theory Problems

Subgraphs, induced subgraphs and minors

A common problem, called the subgraph isomorphism problem, is to find a fixed graph as a subgraph of a given graph. One reason to be interested in this question is that many properties of graphs are inherited from subgraphs, which means that a graph has a property if and only if all its subgraphs have it. Unfortunately, finding maximum subgraphs of a certain type is usually an NP-complete problem. For example:

Finding the largest complete subgraph is called a clique problem.

A similar problem is to find an induced subgraph in a given graph. Again, some important properties are inherited with respect to induced subgraphs, which means that a graph has a property if and only if all induced subgraphs do. Finding maximum induced subgraphs of a certain type is, again, an NP-complete problem. As an example:

Finding the largest induced subgraph without edges or independent set is called the problem of the independent set.

Another new problem is the problem of least content, which is to find a fixed graph as the least of a given graph. A minor or subcontracting of a graph is any graph obtained by taking a subgraph and contracting some edges. Many graph properties are inherited from minors, which means that a graph has it only if all its minors have it. For example, Wagner's theorem states that:

A graph is flat if it contains as a minor neither the full bipartite graph nor the full graph.

A similar problem is the content subdivision problem. A subdivision or homeomorphism of a graph is any graph obtained by subdividing some edges. The subdivision of the content is related to properties of graphs such as "flatness". For example, Kuratowski's theorem states that:

A graph is flat if it contains a subdivision or bipartite graph or full graph.

Another problem in content subdivision is the Kelmans-Seymour conjecture:

Each five connected vertices graph containing a subdivision of the full five vertices graph.

Other problems of sorts have to do with the extent to which various species and generalizations of graphs are determined by their subgraphs of deleted points. For example, the reconstruction conjecture.

Hamiltonian Cycles and Paths

Main article: Hamiltonian Cycle

Example of a hamiltonian cycle.

A cycle is a succession of adjacent edges, where the same edge is not traversed twice, and where the starting point is returned. A Hamiltonian cycle also has to go through all the vertices exactly once (except the vertex from which it starts and to which it arrives).

For example, in a large museum, the ideal would be to go through all the rooms once, that is, to look for a Hamiltonian cycle in the graph that represents the museum (the vertices are the rooms, and the edges are the corridors or doors between they).

There is also talk of a Hamiltonian path if it is not necessary to return to the starting point, as in a museum with a single entrance door. For example, a knight can go through all the squares on a chessboard without going through the same square twice: it is a Hamiltonian path. An example of a Hamiltonian cycle is the dodecahedron graph.

Today, there are no known general methods to find a Hamiltonian cycle in polynomial time, being the brute force search of all possible paths or other methods excessively expensive. There are, however, methods to rule out the existence of cycles or Hamiltonian paths in small graphs.

The problem of determining the existence of Hamiltonian cycles falls within the set of NP-completes.

A graph is Flat if you can draw without crosses of edges. The problem of the three houses and the three wells it has solution on the bull, but not on the plane.

Flat graphs

Main article: Grape plane

When a graph or multigraph can be drawn on a plane without two segments intersecting, it is said to be flat.

A well-known problem is the following: Three houses and three wells are drawn. All the residents of the houses have the right to use the three wells. Since they don't get along at all, they never want to cross paths. Is it possible to trace the nine roads that join the three houses with the three wells without there being any crossings?

Any arrangement of houses, wells and roads implies the presence of at least one crossing.

Sea ${displaystyle K_{n}}$ the full graph with $n$ Vertices, ${displaystyle K_{n,p}}$ is the bipartite graph of $n$ and $p$ Vertices.

The previous game equals to discover if the full bipartite graph ${displaystyle K_{3,3}}$ That's it. Flat, that is, if you can draw on a plane without crossings, being the answer not. In general, a graph may be determined No. is flat, if in its design you can find a similar structure (known as minor) a ${displaystyle K_{5}}$ or ${displaystyle K_{3,3}}$ .

Establishing which graphs are planar is not obvious, and it is a problem that has to do with topology.

Graph coloring

Main article: Graph coloring

Yeah. ${displaystyle G=(V,E)}$ is an undirected graph, a coloring of its own $G$ It happens when we color the vertices of $G$ So if ${displaystyle {a,b}}$ It's an arist in $G$ then. $a$ and $b$ They have different colors (they therefore the adjacent vertices have different colors). The minimum number of colors required for a proper coloring $G$ is the chromatic number $G$ and it is written as ${displaystyle C(G)}$ . Sea $G$ an undirected graph $lambda$ the number of colors available for the own coloring of the vertices $G$ . Our goal is to find a polynomial function ${displaystyle P(G,lambda)}$ , in the variable $lambda$ , called chromatic polynomial $G$ to indicate the number of different colorings of the vertices $G$ using a maximum of $lambda$ colors.

Decomposition of chromatic polynomials. Yeah. ${displaystyle G=(V,E)}$ is a related graph and ${displaystyle ein E}$ , then ${displaystyle P(G,lambda)=P(G+e,lambda)+P(G/e,lambda)}$ Where ${displaystyle G/e}$ is the graph obtained by contraction of edges.

For any graph $G$ , the constant term in ${displaystyle P(G,lambda)}$ That's it. ${displaystyle 0}$ .

Sea ${displaystyle G=(V,E)land |E|=0}$ the sum of the coefficients ${displaystyle P(G,lambda)}$ That's it. ${displaystyle 0}$ .

Sea ${displaystyle G=(V,E)}$ such as ${displaystyle {a,b}in Eland {a,b}=enot in E}$ We write ${displaystyle G+e}$ for the graph obtained from $G$ by adding the edge ${displaystyle e={a,b}}$ . By identifying the vertices to and b in $G$ We get the subgraph. ${displaystyle G++,e}$ of $G$ .

Four Color Theorem

Main article: Theorem of the four colors

Colored map with 4-colored.

Dual graph associated with the map with a 4-vertice coloring.

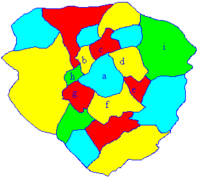
This famous problem concerning the graphs deals with the amount of colors that are necessary to draw a political map, with the obvious condition that two adjacent countries cannot have the same color. Countries are supposed to be one piece, and the world is spherical or flat. The following map shows that three colors are not enough: if you start with the central country $a$ and strives one to use the least number of colors, then in the crown around $a$ alternate two colors. Getting to the country $h$ you have to enter a fourth color. The same happens in $i$ if the same method is used. However, if the map has toroid shape, the theorem states that with four colors it is always possible to perform the coloring with the required characteristics.

The precise shape of each country does not matter; the only relevant thing is to know which country touches which other. These data are included in the graph where the vertices are the countries and the edges connect those that are just adjacent. Then the question is equivalent to attributing to each vertex a different color from that of its neighbors.

We have seen that three colors are not enough, and proving that five always arrives is quite easy. But the four color theorem is not obvious at all. Proof of this is that computers have had to be used to finish the demonstration (a program has been made that allowed a multitude of cases to be verified, which saved mathematicians a lot of time). It was the first time that the mathematical community accepted a computer-assisted proof, which created some controversy within the community at the time.

Characterization of graphs

Simple graph

A graph is simple if there is at most one edge joining any two vertices. This is equivalent to saying that any edge is the only one that joins two specific vertices.

A graph that is not simple is called a multigraph.

In graph theory, the concept of a simple graph is widely used in the definition of other entities, such as complete graphs, complete bipartite graphs, trees and others.

Definitions provide a logical formalization to abstract or natural facts, many times already defined intuitively. In this case, the simple graph image is easy to recognize from another that is not; either by the presence of ties or more than one edge between the pairs of vertices.

Connected graphs

A graph is connected if each pair of vertices is connected by a path; that is, if for any pair of vertices (a, b), there is at least one possible path from a to b.

A graph is doubly connected if each pair of vertices is connected by at least two disjoint paths; that is, it is connected and there is no vertex such that when it is removed the resulting graph is disconnected.

It is possible to determine if a graph is connected using a Broadcast Search (BFS) or Depth Search (DFS) algorithm.

In mathematical terms, the property of a (strongly) connected graph allows establishing an equivalence relation for its vertices, which leads to a partition of these into "(strongly) connected components", that is, portions of the graph, which are (strongly) connected when considered as isolated graphs. This property is important for many proofs in graph theory.

Related and non-related

Complete graphs

Main article: Full Graph

A graph is complete if there are edges joining all possible pairs of vertices. That is, every pair of vertices (a, b) must have an edge e that joins them.

The set of the complete graphs is usually called $K$ , being ${displaystyle K_{n}}$ the full graph $n$ Vertices.

A ${displaystyle K_{n}}$ , i.e., full graph $n$ Vertices has exactly ${displaystyle {frac {n(n-1)}{2}}}$ Aristas.

The graphic representation of the ${displaystyle K_{n}}$ like the vertices of a regular polygon realizes its peculiar structure.

Bipartite graphs

Main article: Bipartite Graph

A G graph is bipartite if you can express ${displaystyle G={V_{1}cup V_{2},A}}$ (i.e., its vertices are the union of two groups of vertices), under the following conditions:

$V_{1}$ and $V_2$ They are disjoint and not empty.
Each arist of $A$ a vertice of $V_{1}$ with one $V_2$ .
There are no edges joining two elements of $V_{1}$ analogous to $V_2$ .

Under these conditions, the graph is considered bipartite, and can be informally described as the graph that joins or relates two sets of different elements, such as those resulting from the exercises and puzzles in which an element from column A must be joined with an element in column B.

Graph Homeomorphism

Main article: Homeomorphism of graphs

Two graphs ${displaystyle G_{1}}$ and ${displaystyle G_{2}}$ are homeomorphs if both can be obtained from the same graph with a succession of elemental subdivisions of edges.

Trees

Main article: Tree (grave theory)

Example of tree.

A graph that has no cycles and connects all points is called a tree. In a graph with n vertices, the trees have exactly n - 1 edges, and there are n^n-2 possible trees. Its importance lies in the fact that trees are graphs that connect all the vertices using the fewest possible number of edges. An important field of application of the study of it is found in the phylogenetic analysis, that of the filiation of entities that derive from each other in an evolutionary process, which is applied above all to the investigation of the relationship between species; although it has also been used, for example, in the study of the relationship between languages.

Weighted or labeled graphs

In many cases, it is necessary to attribute to each edge a specific number, called valuation, weighting or cost depending on the context, and thus obtains a valued graph. Formally, it is a graph with a function v: A → R₊.

For example, a trade representative has to visit n cities connected by roads; their foreseeable interest will be to minimize the distance traveled (or time, if traffic jams can be foreseen). The corresponding graph will have the cities as vertices, the roads as edges, and the valuation will be the distance between them.

Diameter

The figure shows that K₄ is flat (deviating the edge ab outside the square), which K₅ It's not, and K₃,₂ it is also (detours in gray).

In a graph, the distance between two vertices is the smallest number of edges of a path between them. The diameter, in a figure such as a graph, is the greatest distance between all the pairs of points in the figure.

The diameter of the ${displaystyle K_{n}}$ It's 1, and that's ${displaystyle K_{n,p}}$ It's 2. An infinite diameter can mean that the graph has an infinity of vertices or simply is not related. It may also be considered Average diameterlike the average distance between two vertices.

An application of this concept is the hypothesis known as the six degrees of separation, which states that, if each of the inhabitants of the Earth is represented by a vertex and two people are connected by an edge if they know each other personally, The distance between two people chosen at random among all the inhabitants of the Earth is six edges or less.

The Internet allows us to see the idea of diameter from another perspective: consider, for example, that if sites that do not have links are discarded, and two web pages are chosen at random, one would wonder how many web pages web i>clicks you can go from the first site to the second. If it is assumed that from any site that links to other sites you can reach any other, then the largest number of clicks needed to get from any web to another would be the "diameter" of the Network, seen as a graph whose vertices are the sites, and whose edges are the links between the sites.

This concept better reflects the complexity of a network than the number of its elements.

Applications

Graph theory is key in sociometry and social network analysis. It has also been used in various areas of the social sciences, such as anthropology, social psychology, communication, business, research of organizations and geography.

Thanks to graph theory, various problems can be solved, such as the synthesis of sequential circuits, counters or opening systems. It is used for different areas such as Computer Drawing or Engineering areas.

Graphs are also used to model routes such as that of a bus line through the streets of a city, in which optimal paths for the route can be obtained by applying various algorithms such as Floyd's algorithm.

For the administration of projects, we use techniques such as the program review and evaluation technique (PERT) in which they are modeled using graphs and optimizing the times to specify them.

An important application of graph theory is in the field of computing, since it has served to solve important and complex algorithms. A clear example is the Dijkstra Algorithm, used to determine the shortest path in a graph with certain weights on its vertices.

Within this field, a graph is considered a TAD abstract data type.

The American scientist Donald Knuth established planar graphs as the basis of certain studies and discoveries made by him.

On the other hand, the Kruskal Algorithm stands out, which allows us to search for a subset of edges that includes all the vertices, establishing as a minimum the value of the edges.

It is used in production control problems, to design computer networks, to design modern electronic modules and to design physical systems with localized parameters (mechanical, acoustic and electrical).

Used for solving genetic problems and projection automation problems (SAPR). Mathematical support of modern systems for information processing. Helps in nuclear research (Feynman diagram technique).

Graphs are important in the study of biology and habitat. The vertex represents a habitat and the edges (or "edges" in English) represent the paths of animals or migrations. With this information, scientists can understand how this may change or affect species in their habitat.

Conceptual maps
Metro station plan.
Highway plan.
Electric circuit
Sociogram of a social network
Computer network topology
Organizational charts
Isomeros
Mobile phone network architecture
Direct elimination Draws (e.g. tennis)

Important algorithms

Search algorithm in width (BFS)
In-depth search algorithm (DFS)
Search algorithm A*
Algorithm of the nearest neighbor
Topological ordination of a graph
Calculation algorithm of strongly related components of a graph
Algoritmo de Dijkstra
Bellman-Ford Algorithm
Algorithm of Prim
Ford-Fulkerson Algorithm
Kruskal Algorithm
Floyd-Warshall Algorithm

Relevant researchers in graph theory

Alon, Noga
Berge, Claude
Bollobás, Béla
Brightwell, Graham
Chung, Fan
Dirac, Gabriel Andrew
Dijkstra, Edsger
Edmonds, Jack
Erdős, Paul
Euler, Leonhard
Faudree, Ralph
Golumbic, Martin
Graham, Ronald
Harary, Frank
Heawood, Percy John
Kaufmann, Walter Arnold
Kőnig, Dénes
Kuratowski, Kazimierz
Lovász, Laszló
Nešetřil, Jaroslav
Rényi, Alfréd
Ringel, Gerhard
Robertson, Neil
Seymour, Paul
Szemerédi, Endre
Thomas, Robin
Thomassen, Carsten
Turan, Pale
Tutte, W. T.
Whitney, Hassler

Contenido relacionado

Más resultados...