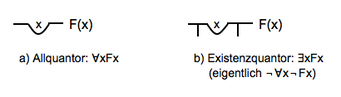Gottlob Frege
Friedrich Ludwig Gottlob Frege (8 November 1848 in Wismar - 26 July 1925 in Bad Kleinen) was a German mathematician, logician, and philosopher. He is considered the father of mathematical logic and analytical philosophy, concentrating on the philosophy of language and mathematics. Frege spent his career in relative obscurity as a professor of mathematics at the University of Jena, long ignored by the philosophical and mathematical community. It is mainly thanks to Giuseppe Peano (1858-1932) and Bertrand Russell (1872-1970), who did a great deal of popularizing Frege's work, that Frege became known to later generations of philosophers and mathematicians.
Frege devised a logistical program aimed at exploring the logical and philosophical foundations of mathematics and natural language. He was convinced that mathematics and language could be reduced to logic. To demonstrate this end, Frege explored the logical foundations of both fields, and in the process gave birth to modern logic (as opposed to the classical logic that had prevailed since Aristotle), mathematical logic, and the early modern works of the philosophy of language. His philosophical interests, his simple, clear, and rigorous style, and his influence on Bertrand Russell, Ludwig Wittgenstein, and the Vienna Circle were the seeds of analytic philosophy.
Frege's two seminal works are his Begriffsschrift (1879, usually translated as Ideography), which laid the foundations of modern logic, and his Grundlagen der Arithmetik (1884, Fundamentals of Arithmetic), where he laid down the philosophical foundations of mathematics. His most widely read work today is his seminal article Über Sinn und Bedeutung (1892, On Sense and Reference ), a fundamental work in the philosophy of language.
Biography
Birth and formation
Frege was born in 1848 in Wismar, then belonging to the Grand Duchy of Mecklenburg-Schwerin, present-day Germany. Her father, Carl (Karl) Alexander Frege (1809–1866), was the co-founder and director of a girls' college. On Carl's death in 1866, the college became headed by her mother Auguste Wilhelmine Sophie Frege (née Bialloblotzky, 1815-1898), a descendant of a Polish noble family and, through her mother's side, the humanist Philipp Melanchthon.
During his childhood, Frege was exposed to many of the aspects that would mark his philosophical career. For example, his father wrote a textbook on the German language entitled Hülfsbuch zum Unterrichte in der deutschen Sprache für Kinder von 9 bis 13 Jahren (2 ed., Wismar 1850; 3rd ed., Wismar and Ludwigslust: Hinstorff, 1862). The first section of that book deals with the logical structure of language.
Frege studied at the gymnasium in Wismar, graduating in 1869. It was his professor of literature, Gustav Adolf Leo Sachse (1843-1909), who insisted that Frege continue his studies in natural sciences at the University of Jena.
Frege enrolled in mathematics at the University of Jena in the spring of 1869 as a citizen of the North German Confederation. He studied for two years in Jena, where he attended 20 subjects, mostly in mathematics and physics, although he also attended classes in Kantian philosophy. Frege was a student of the physicists Christian Philipp Karl Snell (1806-1886) and Hermann Karl Julius Traugott Schaeffer (1824-1900), and of the Kantian philosopher Kuno Fischer (1824-1907). His most important teacher, however, was the physicist Ernst Karl Abbe (1840–1905), who taught gravitation, electrodynamics, mechanics of solids, and analysis of complex variables. Frege maintained a close friendship with Abbe, who would act as Frege's mentor throughout his career.
Abbe was a crucial figure in Jena. He had helped the Zeiss family establish the Carl Zeiss AG optical products company, and as its technical director from 1866 he had revolutionized its production into one of the great German business conglomerates. Abbe had been appointed director of the Carl Zeiss Foundation, which received almost half of the profits of the optical products company Carl Zeiss AG, and used his position to promote scientific research. Frege would be one of the major beneficiaries of the generosity of the Zeiss Foundation via Abbe.
In 1871, after graduating from Jena, Frege went on to study at the University of Göttingen, then the most reputable university in mathematics. He studied under Rudolf Friedrich Alfred Clebsch (1833–72; analytic geometry), Ernst Christian Julius Schering (1824–97; theory of functions), Wilhelm Eduard Weber (1804–91; applied physics), Eduard Riecke (1845–1915; electricity), and Hermann Lotze (1817–81; philosophy of religions). Many of Frege's philosophical doctrines have parallels with Lotze's; To what extent Lotze influenced Frege is a debate that continues to this day.
In 1873 Frege obtained his doctorate under Ernst Schering, with a doctoral thesis entitled "Ueber eine geometrische Darstellung der imaginären Gebilde in der Ebene" (& # 34; On a geometric representation of imaginary forms in the plane & # 34;), in which he tried to solve fundamental problems related to the mathematical interpretation of the geometric projection of imaginary points at infinity.
Jena, 1874-1893
In May 1874, Frege returned to Jena after completing his Habilitationsschrift with a thesis on complex number theory entitled Rechnungsmethoden, die sich auf einer Erweiterung des Größenbegriffes Gründen ("Calculation methods based on a generalization of the concept of size"). He had obtained through Abbe the position of privatdozent, an unpaid position that was then the first echelon of the academic career in Germany.
Ideography (1874)
During his early years in Jena, Frege taught mathematics. Similarly, Frege's early work was in complex analysis and geometry, where he seemed to have a promising career. What led him to make the leap into the philosophy of mathematics is not clear. It seems that his interest in the philosophical foundations of mathematics was relatively early, and that he began to study the mathematical justification of integers upon his return to Jena. In this process, he had to realize that contemporary mathematics was incapable of offering a formal justification, which could have led him to develop a new type of logic capable of addressing this problem. This could have led to the results he presented in his Ideography.
It seems that in the course of these preliminary investigations, Frege came to the conclusion that arithmetic had to be part of (or could be reduced to) formal logic. As he would reflect later, a person's ability to become familiar with natural numbers could not be related to his direct experience or to geometric space, but to language and the analytical reasoning capacity generally known as logic. This type of philosophical interpretation of mathematics is commonly known as logicism.
In 1879, Frege established himself as one of the foremost advocates of this school by publishing his first major work, the Ideography (Begriffsschrift). The Ideography that gives the work its name refers to the set of symbols and the formal syntax that Frege developed in order to clarify the logical relationships contained in ordinary language. Since Aristotle, logic had been based on the propositional calculus, based on which the truth or falsity of a sentence was established by means of a series of logical operators (negation, conjunction, disjunction,...) that allowed syllogisms to be developed.
Frege's Ideography contained the first systematic treatment of propositional logic, which was introduced in an axiomatic form, by means of which all the laws of logic could be deduced. Frege's greatest contribution was, if anything, the invention of quantification theory. Based on this, Frege was able to expand the scope of logical operators to be able to study the logical validity of expressions containing statements such as all, nothing, some , anyone, etc. This was a milestone in the history of formal logic, and the greatest contribution to the field since Aristotle.
The notation that Frege introduced in his Ideography, although elegant, was difficult to reproduce in print, and very laborious and extensive: it was tabular and two-dimensional, which was not appreciated even by publishers and not by readers of the book. Frege was furthermore unable to separate his complex notation from the semantics and syntactic logic that he exemplified. Hidden under a very difficult to penetrate notation, most of the theorems of propositional logic and the many crucial ideas that he developed in Ideography were completely ignored by the academic community.
In fact, Ideography was met with unusual hostility, generally caused by the difficulty of the notation it used. Furthermore, Frege had openly ignored the recent work of George Boole and Ernst Schröder on formal logic. Although the work of both Boole and Schröder was primarily an attempt to algebrify classical logic, Frege made no attempt to compare their systems to his own. This meant that his creation of propositional and second-order logic was hidden from most of the public under a patina of notation. Schröder in particular was very hostile; In his review of the Ideography, he likened the notation to "introducing notions of Japanese while doing nothing better than Boolean, and doing many things worse. " >
Although poorly received, the Ideography earned him, with the help of Abbe, Frege to get the teaching post he would occupy until his retirement. Between 1879 and 1884 Frege was engaged in responding to hostile reviews of the Begriffsschrift and trying to explain how this work differed from Boolean.
Grundlagen (1884)
In order to avoid the criticism his ideographic notation had received, Frege wrote his next great work, the Grundlagen der Arithmetik ("Fundamental Laws of Arithmetic") in a completely different style, avoiding the use of a symbolic language. The Grundlagen is the first work where Frege proposes that arithmetic is derivable from logic although, due to criticisms of the Begriffsschrift, Frege's defense of this thesis is not entirely formal.
Although the Grundlagen is perhaps Frege's most important work, its reception was even colder than that of the Begriffsschrift: it received only three reviews, and all of them were hostile It is not clear why the Grundlagen was so coldly received. It has been thought that, having abandoned all symbolic notation, its content might still have been too technical for philosophers, and too philosophical for mathematicians working in this field. Dedekind ignored the book entirely, Cantor criticized it hostilely, and Hilbert rejected it outright.
Despite the general misunderstanding, the Grundlagen proposes two totally radical theses: on the one hand, that each number is an object that exists by itself; on the other, that assigning a number to a sentence is an assertion about a concept. This means that Frege rejected that numbers were a property belonging to an individual or a collective, and that he also rejected that numbers were a subjective property, dependent on the individual. This radically separated logic from psychology (something that empiricist philosophers had abused), and from epistemology (something frequent among rationalist philosophers in the Descartes tradition).
In 1887, he married, belatedly, Margarete Katharina Sophia Anna Liesebe (1856-1904). Although the details of his private life are unknown, they would have two children who would die in infancy, and they would adopt a boy, Alfred Frege.
The decade that followed the publication of the Grundlagen was a productive period for Frege. It is at this time that he focuses on studying the philosophy of language, where through three articles published in 1891 and 1892 he would forever change the field. The most important of these is Über Sinn und Bedeutung (& # 34; On Sense and Reference & # 34;), where Frege draws a distinction between what he calls the sense of an expression, and his reference. According to Frege, sense and reference are two different aspects of meaning. For him, both object and concept expressions have a reference (an object to which it refers) and a meaning (a way of speaking about that object).
Grundgesetze and final stage (1893-1925)
Frege's last great work was the Grundgesetze der Arithmetik ("Basic Laws of Arithmetic"), the first volume of which appeared in 1893. In this book, Frege set out to to formally construct arithmetic from logic. This should have been his greatest achievement: proving that mathematics was reducible to (and deductible from) logic, something he had already outlined in the Grundlagen and to which he had devoted the entire career of him The Grundgesetze ran into two major problems. On the one hand, chastened by the failure of the Grundlagen and the Begriffsschrift, no publisher wanted to publish the work. Frege eventually managed to dissuade Hermann Pohle, a publisher from Jena who had published articles of his earlier, that he agreed to print the Grundgesetze, but Pohle only agreed on the condition of publishing it in two volumes, publishing the second volume only if the first was successful.
As with the Grundlagen, the first volume of the Grundgesetze was received coldly. This delayed the publication of the second volume by a decade. Despite this, his publication earned Frege promotion to an honorary professorship at Jena, financed by a substantial stipend from the Carl Zeiss Foundation, achieved through the intercession of his Ernst Abbe.
Despite its editorial failure, the Grundgesetze managed to attract the attention of the international community to Frege's work. Its publication spurred a controversy with the Italian mathematician Giuseppe Peano, who had to modify his own axiomatization of arithmetic in order to accommodate Frege's criticisms and theses of it. The controversy with Peano attracted the attention of Bertrand Russell, then a young philosopher at Trinity College, Cambridge University.
Between 1893 and 1903, Frege wrote bitter articles criticizing all the philosophers and mathematicians who had previously criticized his work. He wrote a hostile review against the Philosophie der Arithmetik of Edmund Husserl, who embraced Frege's criticisms of his work and abandoned his mathematical psychologism in favor of Frege's logicist theses.
The other great problem of the Grundgesetze was revealed in 1902, when the second volume of the Grundgesetze was in print. Frege received a letter from Bertrand Russell in which Russell pointed out that the fifth axiom of the Grundgesetze made the whole system inconsistent. Russell's letter, dated June 16, 1902, began:
Dear fellow:
I've known about you Grundgesetze for a year and a half, but it has only been now that I have been able to find time for the detailed study I intend to devote to your writings. I totally agree with you in all its main points, in particular in your rejection of any psychological element in logic, and in the value you assign to a conceptual notation for the foundations of mathematics and of the formal logic that, in passing, can hardly be distinguished. In many details, I find in the discussions, distinctions and definitions of your writings everything that one seeks in vain in other logics. In particular, regarding functions (section 9 of your Conceptual) I have come independently to the same conclusions even in detail. I found a difficulty only at one point. Affirmations (p. 17) that a function can also constitute the undetermined element. This is what I used to believe, but this point of view seems to me now doubtful because of the following contradictionSea w the preached of being a preacher who cannot be preached of himself. Can you? w to be a preacher of himself? A contradiction is followed from both responses. We must therefore conclude that w is not a preacher. Likewise, There's no class. (in its entirety) of all classes which, as a whole, are not members of themselves. From this I conclude that under certain circumstances a definable set does not form a complete set.
The fifth axiom stated that if every A is a B, and every B is an A, then the class of Ass is identical to the class of Bss. Russell, by means of Russell's paradox, pointed out that this axiom allowed the existence of a class of all classes of things that are not members of themselves; but if a thing is a member of itself, then it is not a member of itself; but if it is not a member of itself, then it is a member of that class, which is contradictory. Thus, Russell pointed out that Frege's system could not be logically consistent.
Frege received Russell's letter with genuine astonishment. Unlike Peano, to whom Russell had also communicated his paradox, Frege recognized the problem with intellectual integrity and, in order to remedy it, tried to relax i> the fifth axiom of his system in one of the appendices of the second volume of Grundgesetze, where he discussed Russell's paradox and its possible solution. His solution also turned out to be logically inconsistent, although Frege held the contrary for a few years.
Before his retirement in 1918, Frege had abandoned any claim to having solved the problem, and accepted the failure of his logician system. By then, the mathematical logic that Frege had pioneered had captured the attention of the philosophical and mathematical community, although Frege continued to be ignored. He devoted the rest of his life to addressing the relationship between logic and psychology, in a series of articles compiled as Logical Investigations (1919-1923). Most of his writings from this period were not published until 1969.
He died in 1925 in Bad Kleinen, where he had retired after retirement, leaving all his manuscripts to his adoptive son Alfred.
Diary and personal opinions
Frege was a reserved and introverted person. His students said that he taught class looking at the blackboard, peppering his explanations from time to time with deeply sarcastic comments. His character and relative obscurity mean that his personal views and character are only known through his own manuscripts, in particular his private journal, which was recovered by Michael Dummett in the 1970s.
Frege's philosophical work was extremely technical in nature, lacking in any practical aspect, so much so that the English philosopher and biographer Dummett, one of Frege's great popularizers, expressed his "dismay to discover, while reading Frege's journals, that his hero was an anti-Semite." Following the November Revolution of 1918, Frege's political views became more radical. His personal diary during the last years of his life contains extreme right-wing opinions, opposed to the parliamentary system, democracy, liberals, Catholics, the French and Jews, whom he considered should be deprived of their political rights and expelled from Germany. Frege claimed that he had considered himself in the past as a liberal and an admirer of Otto von Bismarck, but came to sympathize with General Ludendorff and Adolf Hitler. Frege also criticized universal suffrage and socialism. Frege was friendly with Jews in real life: one of his students was Gershom Scholem, who was very fond of his professor; and Frege encouraged Ludwig Wittgenstein to go to Cambridge to study. Frege's 1924 diary was published posthumously in 1994. Frege's personal views were ignored by those close to him, since he never expressed them in public.
Thought
In 1879, Frege published his revolutionary work entitled Ideography or Writing of Concepts (Begriffsschrift), in which he laid the foundations of modern mathematical logic, ushering in a new era in this discipline that had remained virtually unchanged since Aristotle. By introducing a new syntax, including so-called quantifiers ("for all" or "for at least one"), he allowed an enormous number of new arguments to be formalized. He was also the first to distinguish the formal characterization of logical laws from their semantic content.
Once the axiomatic principles of logic were established, he undertook the task of building arithmetic on its basis. One problem with Frege's groundbreaking works is the amount of print space his notation requires; It wasn't really until the publication of Alfred North Whitehead and Bertrand Russell's Principia mathematica that the power of formal logic, in a less extensive notation (but requiring many grouping signs) was appreciable.
Logicism
Frege was a defender of logicism, the thesis that mathematics is reducible to logic, in the sense that the truths of mathematics are deducible from the truths of logic. However his defense of logicism was limited in scope, applying it only to arithmetic and set theory, since Frege remained largely Kantian on geometry. His work entitled Basic Laws of Arithmetic ( Grundgesetze der Arithmetik ) was an attempt to carry out the logician project. In 1902, with the corrected proofs of the second volume already in print, he received a letter from Bertrand Russell warning him of a serious inconsistency in his logical system, later known as Russell's paradox.
Frege hurriedly introduced a modification to one of his axioms, which he recorded in an appendix to the work. This blow to the structure of his work practically put an end to his academic activity. Faced with the almost total indifference of his contemporaries, after the death of his wife he secluded himself in his new residence in Bad Kleinen and remained largely anonymous until Bertrand Russell made it known, since having reached the same results as Frege de Independently he was able to understand him and was the first important thinker to appreciate the great value of his work. Despite the fact that the discovery of Russell's paradox ruined Frege's logicist project, Frege continued to work and published a series of important articles, including Thought: A Logical Investigation, where basically the content of the propositions is examined, that objective part that is transmittable to every speaker in a declarative statement. In the 1960s, the Oxford philosopher Michael Dummett published a series of important books on Frege's philosophy that revived interest in Frege's work and reincorporated him into the philosophical debate.
Philosophy of language
Frege's theory of meaning confronts the psychological tradition that assigns mental contents to words as their meanings. Frege confronts this tradition in his article On Sense and Reference, and inaugurates an important tradition in the philosophy of language.
The thesis according to which words are signs of ideas is exposed by John Locke in his Essay Concerning Human Understanding. Locke, starting from the communicative purpose of language, defines words as "signs of internal conceptions". These "inner conceptions", ideas, are entities that are contained in our mind; people through words communicate such ideas. Ideas come from our sensitive experience. For Locke there is no direct relationship between language and the world, but language is a tool with which we communicate our ideas.
For his part, in his article entitled On meaning and reference, Frege begins by asking himself about identity statements, of which he distinguishes two types:
- a = a
- a = b
and reasons like this: statements of type (1) are trivial, but the same is not true of statements of type (2). The identity relationship that appears in these statements cannot be between signs of objects or between objects. If the identity is between objects, the information provided by (1) is not different from that provided by (2). If the relationship occurs between names of objects, then we are not saying anything extralinguistic. So Frege solves this question by distinguishing reference and meaning in expressions. The reference is the object itself that we designate with a sign, the sense expresses the way of giving itself to the object. That is, with (2) we express two different ways of referring to the same object.
While according to the thesis that words are signs of ideas, words signify subjective ideas that are contained in the minds of speakers, the theory of meaning presented by Frege in On Sense and Reference tells us that the signs mean the ways of giving themselves the objects to which we refer with our words. Meaning is an approximation to the object itself. For example, if I utter an expression like "Venus is Hesperus", it is saying that the object to which "Venus" is the same object that "Héspero" refers to. Both expressions are names for the same object. However, Venus is an internationally known name, with which some speakers will associate some properties, while the name "Héspero" different properties will be assigned to it. In this way someone could come to think that it is false.
Since, according to Locke's thesis, our words are signs of ideas that are in fact in our minds, Frege breaks with this psychologism, defending instead a more objective and precise realism when determining the meanings of our expressions. For Frege our words refer to objects and also express ways of giving themselves such objects, that is, they have meaning. Now, is the meaning of an expression a subjective representation of the speaker? No, because Frege says: "From the reference and the meaning of the sign we must distinguish the representation associated with it". In this way, the reference of a sign is an object, if the object is sensible, the representation that I have is nothing more than an "internal image" built from the memory of the sensations that such an object produced in me, and in this the subjective representation of the reference differs.
But what about the meaning? Neither. The meaning of a sign "may be the common property of many" while "representation is subjective". The sense of an expression is understood to the extent that one has some knowledge of the referent.
So far we have talked about reference as if all our expressions refer to an object. However, for Frege this is not the case. There are expressions that seem to point towards an object, which makes us conceive of its meaning without such a reference existing. This is the case of expressions such as the "greatest natural number" or "the most useless politician", since for each natural number there is always another greater, and for each useless politician there is always another that is more so. In spite of everything, the meanings of this class of expressions are not private ideas in the minds of the speakers either.
Frege flatly rejects the thesis that words are signs of ideas. I have taken the thesis as Locke exposes it, such as that ideas are entities that are contained in the minds of the speakers. Only the speaker himself has access to these ideas, and we use words as signs of these ideas to communicate them. Frege breaks with this psychologism, according to which meanings and concepts are private entities, to open up to a new Platonic paradigm: the realism of meaning, from where he defends that our words refer to objects in the world, have reference and, also, sense. The sense is given by the knowledge that one has of the reference, without it following from this that it is something subjective, regarding this Frege says that "humanity has a common treasure of thoughts, which it transmits from one generation to another", that is, the senses, the meanings of the words belong to communities of speakers and not to the minds of individuals; what is unique to speakers are their subjective representations, of which words are not signs.
Influence
Frege's work on the foundations of mathematics directly influenced the Principia Mathematica of Bertrand Russell and Alfred North Whitehead. Ludwig Wittgenstein and Edmund Husserl were also other philosophers deeply influenced by Frege. Rudolf Carnap endorsed many of Frege's logicist theses, and developed much of Frege's philosophy on Frege's. In this way, Frege became the intellectual godfather of the Vienna circle. Frege is therefore considered the father of the analytic school of philosophy.
Frege was a key figure in the philosophy of language. The distinction between sense and reference and between concept and object are due to him. In 1930, Gödel's incompleteness theorems undermined part of Frege's logicalist project. The theorems show that for any formal system that is powerful enough to express arithmetic, there will be true propositions in the system that cannot be proved, nor their denials disproved. Despite this, Frege's contribution as the great pioneer of mathematical logic is openly recognized.
Gilles Deleuze articulates his Logic of Sense based on the infinite proliferation of verbal entities or Frege's paradox, according to which "given a proposition, its sense can always be taken as what is designated by another proposition".
Work
- Ideography (1879) (Begriffsschrift)
- The foundations of arithmetic (1884) (Die Grundlagen der Arithmetik)
- Basic laws of arithmetic (two volumes) (1893-1903)Grundgesetze der Arithmetik)
- On meaning and reference (1892) (Über Sinn und Bedeutung)
Contenido relacionado
Gottfried leibniz
Stephen Kleene
Universal quantizer
Raymond smullyan
Gerhard gentzen