Goo
The viscosity of a fluid is a measure of its resistance to gradual deformations produced by shear stresses or tensile stresses in a fluid. For example, honey has a much higher dynamic viscosity than water. The dynamic viscosity of honey is 70 centipoise and the dynamic viscosity of water is 1 centipoise at room temperature.
Viscosity is a characteristic physical property of all fluids, which emerges from collisions between fluid particles that move at different speeds, causing resistance to their movement according to the kinetic theory. When a fluid is forced through a smooth tube, the particles that make up the fluid move faster near the long axis of the tube, and slower near the walls. Therefore, it is necessary that there are some shear stresses to overcome the resistance due to the friction between the layers of the liquid and the condition of no slip at the edge of the surface, and that the fluid continues to move through the tube of minimum roughness.. Otherwise, there would be no movement.
A fluid that has no viscosity is a superfluid. It happens that in certain conditions the fluid does not have the resistance to flow or it is very low and the zero viscosity model is an approximation that is verified experimentally.
The viscosity of some fluids is measured experimentally with viscometers and rheometers. The part of physics that studies the deformation due to external forces in fluids is rheology. The internal forces are the reactions that are generated by the existing friction between the layers of fluid.
It only exists in liquids and gases (fluids). It is represented by the Greek letter μ. It is defined as the ratio of the local negative velocity gradient, which is the driving force for momentum transport, to the net momentum flux, which is the ratio of shear stress to plate area traversed by the plates. molecules. This relationship is also called the viscous momentum flux, and it appears to follow the direction of decreasing velocity, that is, it goes from a region of high velocity to a region of low velocity. In case the flow is turbulent, the Boussinesque Eddy Viscosity is added to the molecular viscosity, which means that the effect of Turbulent Flow is added to that of Laminar Flow. This is a function of position.
Etymology
The word "Viscosity" It comes from the Latin viscum ("mistletoe"). Viscum also refers to the viscous glue derived from mistletoe berries.
Liquids
Fluids that follow Newton's laws are called Newtonian fluids. Liquids that do not follow this form are pastes, suspensions, and high molecular weight polymers. Viscosity generally decreases with increasing temperature because the distance between the molecules is small and they travel very small distances between them, so effective shock is the form of transfer.
Gas
The viscosity of gases with low density increases with increasing temperature.
Kinematic viscosity
Another viscosity is also known, called kinematic viscosity, and is represented by the Greek letter ν (ni). To calculate the kinematic viscosity, it is enough to divide the dynamic viscosity by the density of the fluid:
.. =μ μ ρ ρ {displaystyle nu ={frac {mu }{rho }}}}
[chuckles].. ]=(lorngitud)2tiempor=m2s=N⋅ ⋅ mkg⋅ ⋅ s=Jkg⋅ ⋅ s={displaystyle {nu}={frac {(longitude)}}{time}}{{{frac} {{m^{2}}{s}}}=mathrm {{frac {rm} {ncdot m}}}{{{rm {kg}}}{cdot}}{m {rm {w}{c}{c}{c}}}{ specific energy multiplied by time.
![{displaystyle [nu ]={frac {(longitud)^{2}}{tiempo}}={frac {m^{2}}{s}}=mathrm {{frac {rm {Ncdot m}}{rm {kg}}}cdot s} =mathrm {{frac {rm {J}}{rm {kg}}}cdot s} =}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a24851dc9ded99b48f4942113cc6fc3bdd08cbdc)
Non-Newtonian fluid
These are gases and polymerized liquids, asphaltic substances, pasty materials, crystalline materials and suspensions. If the viscosity decreases with increasing velocity gradient, the behavior is called pseudoplastic and dilatant when it increases with increasing said gradient. If the viscosity is independent of the velocity gradient, the fluid behaves as a Newtonian. Various models have been proposed to express the relationship that exists, at steady state, between the negative local velocity gradient and the viscous flow density of momentum. Positive empirical parameters can be obtained by correlating the viscous flow density of momentum with the negative local velocity gradient at constant temperature and pressure. They arise from empiricism when fitting the curves and it is risky to use them in a range other than the one obtained. The values of the rheological parameters are also a function of the temperature, pressure and local negative velocity gradient, so it is necessary to clarify the conditions in which they are obtained. When the state is not steady, if by suddenly applying a shear force the viscosity begins to decrease the fluid is thixotropic and if it begins to increase it is rheopectic. When the shear effort ceases, it partially recovers its properties, it is viscoelastic.
Bingham's model
Bingham plastic remains rigid as long as the shear stress is less than a certain value, above which it behaves similar to a Newtonian fluid. It is used for pastes and fine suspensions.
Waele's Ostwald Model
Used to model dilatant and pseudoplastic fluids by converting the viscosity into a function of the local velocity gradient such that as the local velocity increases, the viscous flow density decreases for pseudoplastic fluids and increases for dilatant fluids.
Eyring's model
Eyring's model predicts the behavior of pseudoplastic fluids for finite values of viscous flow density and becomes Newton's law of viscosity as the viscous flow density approaches zero.
Ellis model
It presents great flexibility because it becomes Newton's Law and the Power Law depending on the values that the constants acquire.
Reiner-Philippoff model
For very low or very high values of the local velocity gradient, it obeys Newton's Law.
Viscosity explained
Let's imagine a solid (non-fluid) block subjected to a tangential force (for example: an eraser on which the palm of the hand is placed and pushed parallel to the table). In this case, the solid material (a) opposes resistance to the applied force, but deforms (b) all the more the lower its rigidity.
If we imagine that the eraser is made up of thin layers one on top of the other, the result of the deformation is the relative displacement of some layers with respect to the adjacent ones, as shown in figure (c).
In liquids, the slight friction between adjacent layers is called viscosity. It is its small magnitude that gives the fluid its peculiar characteristics; so, for example, if we drag the surface of a liquid with the palm of the hand as we did with the eraser, the lower layers will not move or will move much more slowly than the surface since they are dragged by the effect of the small tangential resistance, while the upper layers flow easily. Similarly, if we stir with a spoon a large container with water in which we have deposited small pieces of cork, we will observe that when stirring in the center the periphery also moves and when stirring in the periphery the cork pieces in the center also rotate; again, the cylindrical layers of water move due to viscosity, slowing down as we move further away from the spoon.
It should be noted that viscosity only manifests itself in moving fluids, since when the fluid is at rest it adopts a form in which the tangential forces that it cannot resist do not act. That is why when a container is filled with a liquid, its surface remains flat, that is, perpendicular to the only force acting at that moment, gravity, therefore without any tangential component.
If the viscosity were very high, the friction between adjacent layers would be too, which means that they could not move relative to each other or would do so very little, that is, we would be dealing with a solid. If, on the other hand, the viscosity were zero, we would be facing a superfluid that has remarkable properties such as escaping from containers even if they are not full (see Helium-II).
Viscosity is characteristic of all fluids, both liquids and gases, although in the latter case its effect is usually negligible, they are closer to being ideal fluids.
Quantitative Expressions
There are various models of viscosity applicable to substances that exhibit viscous behaviors of different types. The easiest model or type of viscous fluid to characterize is the Newtonian fluid, which is a linear model (between the velocity gradient and tangential stresses) but there are also non-linear models with shear thinning or thickening or such as Bingham plastics..
Newtonian Fluid
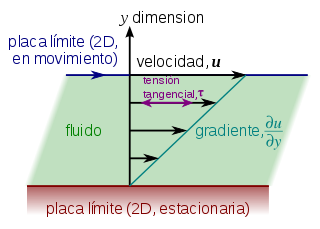
In a newtonian fluid the strength experienced by a moving plate, at constant speed (u){displaystyle (u)} by the surface of a fluid is given by:
| Symbol | Name |
|---|---|
| F{displaystyle F} | Cutting force |
| μ μ {displaystyle mu } | Dynamic viscosity |
| A{displaystyle A} | Area |
| u{displaystyle u} | Constant speed |
| and{displaystyle and} | Separation |
| uand{displaystyle {frac {u}{y}}}} | Cutting Deformation Rate (Crying Speed) |
This expression can be rewritten in terms of tangential stresses on the plate as:
Δ Δ xand=μ μ ▪ ▪ u▪ ▪ and{displaystyle tau _{xy}=mu {frac {partial u}{partial y}}}}}
where u{displaystyle u} It's fluid speed.
By plotting the shear stress against the negative local velocity gradient, a straight line is obtained through the origin of coordinates and whose slope is the viscosity at a given temperature and pressure. This occurs in unpolymerized liquids and gases.
Units
Dynamic viscosity, μ
Relates the local stress or tension in a moving fluid with the strain rate of the fluid particles. The viscosity of a fluid is the resistance to which the different sheets slide against each other.
Dynamic viscosity, designated as μ, is measured, in SI units, in pascal-seconds (Pa s), or N s m-2, or kg·m−1·s−1.
In the Cegesimal System the poise (P) is used.
- 1 poise = 1 [P] = 10-1 [Pa·s] = [10]-1 kg·s-1·m-1]
The following are dynamic viscosity values for some fluids:
Gas (to 0 °C): Dynamic viscosity μ [Pa·s]
Hydrogen 0,00084 Air 0.0000174 Xenón 0.000212 Water (20 °C) 0.001
Kinematic viscosity, ν
The cinematic viscosity, designated as Greek ν (ni), is measured in units of the International System, in square meters per second (m2/s){textstyle left({m^{2}}{big /}{s}right)}.
In the Cegesimal System uses stokes (St){textstyle left({St}right)}.
Influence of temperature and pressure
The correlations used are based on the principle of corresponding states. One correlation is the reduced viscosity, that is, the viscosity at a given pressure and temperature divided by the viscosity corresponding to the critical point as a function of the reduced temperature and reduced pressure. It is observed that the viscosity of the gas tends towards the low density limit when the pressure tends to zero at a certain temperature. For most gases it is reached at 1 atm of pressure. The critical viscosity is estimated by the following methods: i) if the value of the viscosity is known for a certain reduced temperature and pressure, if possible in the conditions closest to those sought, the correlation is used. ii) if only the critical values of p-V-T are known, the critical viscosity is estimated empirically. The other correlation is the numeral viscosity, which is the relationship between the viscosity at a certain temperature and pressure divided by the viscosity at the same temperature but at atmospheric pressure as a function of reduced temperature and pressure. The viscosity at atmospheric temperature and pressure is estimated from the Theory of Dilute Gases.