Golden ratio

ImprimirCitar

The golden number arises from the division in two of a segment saving the following proportions: The total length a+b is the longest segment aLike, a is the shortest segment b.

The AB and BC segments are perpendicular and equal to the unit. With center in O we trace the radius circumference 1/2. Finally, joining A with O and prolonging we get P. The AP length is the golden number regarding AB. (EUCLIDES)

The golden ratio, also called the golden number, number of God, extreme and average ratio, golden ratio, golden ratio, golden mean, golden ratio and divine ratio, is an irrational number, represented by the Greek letter φ (phi) (lowercase) or Φ (Phi) (uppercase) in honor of the Greek sculptor Phidias.

Its numerical value, using radicals or decimals, is:

${displaystyle varphi ={frac {1+{sqrt {5}}}{2}}approx 1.618 033 988 749 894ldots }$

Since it is irrational, it is not possible to represent it exactly as a decimal fraction; you can keep calculating figures, but you never reach the last one.

It is also represented by the Greek letter tau (Τ τ), as it is the first letter of the Greek root τομή, which means to shorten, although it is more common to find it represented by the letter fi (phi) (Φ,φ). It is also represented by the lowercase Greek letter alpha.

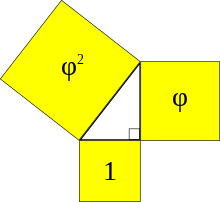
It is an irrational algebraic number (its decimal representation is infinite and it has no period) that has many interesting properties and was discovered in Antiquity, not as an arithmetic expression, but as a relationship or proportion between two segments of a line, that is, a geometric construction. This proportion is found both in some geometric figures and in nature: in the veins of the leaves of some trees, in the thickness of the branches, in the shell of a snail, in the florets of sunflowers, etc. One of its most curious arithmetic properties is that its square (Φ² ≈ 2.61803398874988…) and its reciprocal (1/Φ ≈ 0.61803398874988…) have the same infinite decimal places.

Likewise, an aesthetic character is attributed to objects whose measurements keep the golden ratio. Some even believe it has mystical importance. Throughout history, its inclusion in the design of various works of architecture and other arts has been attributed, although some of these cases have been questioned by scholars of mathematics and art.

Contemporary sculpture in steel elaborated by the sculptor and mathematician Ibo Bonilla. Based on a symbolism, it uses the concept of the golden number in relation to the "Flor of Life" and "Sacred Geometry". It measures 17,8 m (11xx) high and each of the modules of the spiral measures ≈=1.618 m. It's Costa Rica's tallest sculpture.

Definition

The golden ratio is the numerical value of the proportion between two line segments a and b (a longer than b), which fulfill the following relationship:

The total length, adds to the two segments a and bIt's the largest segment. a, what this segment a is the minor b. Written as algebraic equation:

${displaystyle {frac {a+b}{a}}={frac {a}{b}}}$

Being the value of the golden number φ the quotient: $phi =a/b$ . The following geometric problem arises: to divide a segment into two others, so that, by dividing the total length by that of the larger segment, we obtain the same result as by dividing the length of the larger segment by that of the minor.

Calculation of the value of the golden ratio

Two numbers a and b are in the golden ratio if:

Deduction
	1	2
Equations	${displaystyle {frac {a+b}{a}}={frac {a}{b}}}$	${displaystyle varphi ={frac {a}{b}}}$
Simplifying	${displaystyle 1+{frac {b}{a}}={frac {a}{b}}}$
Replacement	${displaystyle 1+varphi ^{-1}=varphi }$
Multiplying ${displaystyle (varphi)}$	${displaystyle varphi +1=varphi ^{2}}$
Clearing	${displaystyle varphi ^{2}-varphi -1=0}$
Positive solution	${displaystyle varphi ={frac {1+{sqrt {5}}}{2}}}$

${displaystyle varphi ={frac {1+{sqrt {5}}}{2}}approx 1{textrm {.}}6180339887498948482045868343656381177203ldots }$

which is the value of the golden number, equivalent to the relationship $a/b$ .

History of the golden ratio

Some authors suggest that the golden ratio is found as a ratio on various Babylonian and Assyrian stelae from around 2000 BCE. C. However, there is no historical documentation indicating that the golden number was consciously used by these artists in the preparation of the stelae. When measuring a complex structure, it is easy to get curious results if you have many measurements available. In addition, for it to be possible to affirm that the golden number is present, the measurements must be taken from significant points of the object, but this is not the case of many hypotheses that defend the presence of the golden number. For all these reasons, Mario Livio concludes that it is highly unlikely that the Babylonians discovered the golden ratio.

Antiquity

The first to make a formal study of the golden ratio was Euclid (c. 300 BC-265 BC), who defined it as follows:

It is said that a straight has been cut in extreme and half reason when the whole straight is to the larger segment as the larger segment is to the smaller segment.
Euclides The Elements Definition 3 of the Sixth Book.

Euclid also showed that this number cannot be described as the ratio of two integers; that is, it is an irrational number.

Plato (c. 428-347 BC) may have studied the golden ratio; however, it may be that he is credited with developing theorems related to the golden ratio because the Greek historian Proclus wrote:

Eudoxo... multiplied the number of theorems related to the section to which Plato originated.
Prochlor in A commentary on the First Book of the Euclid Elements.

Here the word section (τομή) was often interpreted as the golden section. However, starting in the XIX century, this interpretation has been the subject of great controversy and many researchers have come to the conclusion that the The word section had nothing to do with the golden ratio. However, Plato considered that the irrational numbers, discovered by the Pythagoreans, were of particular importance and the key to the physics of the cosmos. This opinion had a great influence on many later philosophers and mathematicians, particularly the Neoplatonists.

Modern Age

In 1509, the Italian mathematician and theologian Luca Pacioli published De Divina Proportione (The Divine Proportion), where he gave five reasons why he considered it appropriate to consider the golden ratio divine:

Oneness; Pacioli compares the unique value of the golden number to the oneness of God.
The fact that it is defined by three straight segments, Pacioli associates it with the Trinity.
The immeasurability; for Pacioli the immeasurability of the golden number and the immeasurability of God are equivalent.
The self-similitude associated with the golden number; Pacioli compares it to the omnipresence and invariability of God.
According to Pacioli, in the same way that God became the Universe through the fifth essence, represented by the dodecahedron, the golden number became the dodecahedron.

In 1525, Albrecht Dürer published Instruction on the measurement with a ruler and compass of flat and solid figures, where he describes how to draw with a ruler and compass the golden spiral based on the golden section, which is known as "Dürer's spiral".

The astronomer Johannes Kepler (1571-1630) developed a Platonic model of the solar system using the Platonic solids, and he spoke of the golden ratio in grand terms:

Geometry has two great treasures: one is the theorem of Pythagoras; the other, the division of a line between the end and its proportional. The first one can compare it to a measure of silver; the second one must call it a precious jewel.
Johannes Kepler in Mysterium Cosmographicum (The cosmic mystery).

The first known use of the adjective aureo, gilt, or gold, to refer to this number is made by the German mathematician Martin Ohm, brother of the famous physicist Georg Simon Ohm, in the second edition of 1835 of his book Die Reine Elementar Matematik (Pure Elementary Mathematics). Ohm writes in a footnote:

One also gets used to calling this division of an arbitrary line in two parts like these the golden section.
Martin Ohm in Die Reine Elementar Matematik (Pure elementary mathematics).

Although the spelling suggests that the term was already in common use by this time, the fact that he did not include it in his first edition suggests that the term may have gained popularity around 1830.

In mathematics texts that dealt with the subject, the usual symbol to represent the golden ratio was τ, from the Greek τομή, which means 'cut or section'. However, the modern denomination Φ or φ was made in 1900 by the mathematician Mark Barr in honor of Phidias, since this was the first letter of his name written in Greek (Φειδίας). This honor was granted to Phidias for the maximum aesthetic value attributed to his sculptures, a property that was also attributed to the golden ratio at that time. Mark Barr and Schooling were responsible for the mathematical appendices to the book The Curves of Life, by Sir Theodore Cook.

The golden ratio in mathematics

Properties and representations

Silver Angle

{displaystyle {frac {360^{circ }}{varphi +{1}}}approx 137{.}5^{circ }}

ratio number aure

Arithmetic properties

${displaystyle textstyle varphi =1.618033988749894848204586834365638117720309...}$ is the only positive real number such that:

varphi ^{2}=varphi +1

φ also possesses the following properties, derived from the previous:

varphi -1={frac {1}{varphi }}

varphi ^{3}={frac {varphi +1}{{varphi -1}}}

{displaystyle varphi ^{2}-{frac {1}{varphi }}=2 }

The powers of the golden number can be expressed according to a sum of powers of lower grades of the same number, established a true recurring succession of powers.

The simplest case is:

{displaystyle varphi ^{n}=varphi ^{n-1}+varphi ^{n-2},}

Whatever. n an integer. This case is a recurring succession of order k = 2, since two previous powers are used.

A recurring equation of order k has the form:

a_{1}u_{{n+k-1}}+a_{2}u_{{n+k-2}}+...+a_{k}u_{n},

where

a_{i},

is any real or complex number and k is a natural number less or equal to n and greater or equal to 1. In the previous case is

scriptstyle k=2,

scriptstyle a_{1}=1,

and

scriptstyle a_{2}=1,

But we can “save” the power immediately above and write:

{displaystyle varphi ^{n}=varphi ^{n-2}+2varphi ^{n-3}+varphi ^{n-4},}

. Here.

{displaystyle scriptstyle k=4,}

{displaystyle scriptstyle a_{1}=0,}

scriptstyle a_{2}=1,

scriptstyle a_{3}=2,

and

scriptstyle a_{4}=1,

If we cancel the two powers immediately above, there is also a recurring formula of order 6:

{displaystyle varphi ^{n}=varphi ^{n-3}+3varphi ^{n-4}+3varphi ^{n-5}+varphi ^{n-6},}

Generally:

{displaystyle varphi ^{n}=sum _{i=0}^{k/2}{{frac {k}{2}} choose i}varphi ^{left[textstyle n-left(textstyle {frac {k}{2}}+iright)right]};qquad k=2j, n, iin mathbb {N} }

In short, any power of the golden number can be considered as the element of a recurring succession of orders 2, 4, 6, 8,..., 2kwhere k It's a natural number. In the recurrent formula, negative powers may appear

varphi

, totally correct. In addition, a negative power

varphi

corresponds to a positive power of its reverse, the golden section.

This curious set of properties and the fact that the significant coefficients are those of the binomial, seem to indicate that between the golden number and the number and there is a kinship.

The golden number ${displaystyle {tfrac {{sqrt {5}}+1}{2}}}$ is the fundamental unit “ε” of the algebraic number body ${mathbb {Q}}left({sqrt {5}}right)$ and the golden section ${displaystyle {tfrac {{sqrt {5}}-1}{2}}}$ is his reverse, « $varepsilon ^{{-1}}$ ». In this extension the "emblematic" number irrational ${sqrt {2}}$ fulfils the following equality:

{sqrt {2}}={frac {{sqrt {5}}+1}{2}}{sqrt {3-{sqrt {5}}}}={frac {{sqrt {5}}-1}{2}}{sqrt {3+{sqrt {5}}}}

Representation by continued fractions

The expression using continued fractions is:

${displaystyle varphi =1+{frac {1}{varphi }}quad longrightarrow quad varphi =1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+{cfrac {1}{1+...}}}}}}}}}$

This iteration is the only one where adding is multiplying and subtracting is dividing. It is also the simplest of all continued fractions and the one with the slowest convergence. This property also means that the golden ratio is a number that is poorly approximated by rationals, which in fact reaches the worst possible degree of approximability by rationals.

That is why it is said that $varphi$ is the farthest number from the rational or the most irrational number. This is why it appears in the theorem of Kolmogórov-Arnold-Moser.

Trigonometric Representation

varphi =1+2sin(pi /10)=1+2sin 18^{circ }

varphi ={1 over 2}csc(pi /10)={1 over 2}csc 18^{circ }

varphi =2cos(pi /5)=2cos 36^{circ }

varphi ={frac {1}{2}}sec {frac {2}{5}},pi ={frac {1}{2}}sec 72^{circ }

{displaystyle varphi ={frac {sin(2pi /5)}{sin(1pi /5)}},={frac {sin(72^{circ })}{sin(36^{circ })}}}

These correspond to the fact that the diagonal of a regular pentagon (distance between two non-consecutive vertices) is φ times the length of its side, and to other similar relationships in the pentagram.

Representation using nested roots

varphi ={sqrt {1+varphi }}quad longrightarrow quad varphi ={sqrt {1+{sqrt {1+{sqrt {1+{sqrt {1+cdots }}}}}}}}

This formula as a particular case of a general identity published by Nathan Altshiller-Court, of the University of Oklahoma, in the American Mathematical Monthly magazine, 1917. The general theorem says that the expression

lim _{{nto infty }}{sqrt {a_{1}+{sqrt {a_{2}+{sqrt {a_{3}+{sqrt {a_{4}+{sqrt {cdots +{sqrt {a_{n}}}}}}}}}}}}}

where $a_{i}=a,$ , is equal to the greater roots of the equation ${displaystyle x^{2}-x-a=0,}$ I mean, ${displaystyle {tfrac {1+{sqrt {1+4a}}}{2}}}$ .

Relation to the Fibonacci sequence

If Fibonacci's number is denoted as F_nand the next number of Fibonacci F_{n + 1}, we discover that, as n increase, this reason oscillates and is alternatively less and greater than the golden reason. We can also note that the continuous fraction that describes the golden number always produces Fibonacci numbers as it increases the number of one in the fraction. For example: ${displaystyle textstyle {frac {3}{2}}=1.5}$ ; ${displaystyle textstyle {frac {8}{5}}=1.6}$ and ${displaystyle textstyle {frac {21}{13}}=1.61538461...}$ which approaches considerably to the golden number. Then you have to:

{displaystyle lim _{nto infty }{frac {F_{n+1}}{F_{n}}}=varphi }

This property was discovered by the German astronomer Johannes Kepler, but more than a hundred years passed before it was proven by the Scottish mathematician Robert Simson.

Later, it was found that any recurring additive sequence of order 2 tends to the same limit. For example, if we take two arbitrary natural numbers, for example 3 and 7, the recurring sequence is: 3, 7, 10, 17, 27, 44, 71, 115, 186, 301,... The quotients of successive terms produce rational approximations that approach asymptotically by excess and by default to the same limit: 44/27 = 1.6296296…; 71/44 = 1.613636…; 301/186 = 1.6182795.

In the mid-19th century, the French mathematician Jacques Philippe Marie Binet rediscovered a formula that was apparently already known to Leonhard Euler, and by another French mathematician, Abraham de Moivre. The formula allows you to find the nth Fibonacci number without the need to produce all the previous numbers. Binet's formula depends exclusively on the golden number:

{displaystyle F_{n}={frac {1}{sqrt {5}}}left[left({frac {1+{sqrt {5}}}{2}}right)^{n}-left({frac {1-{sqrt {5}}}{2}}right)^{n}right]quad ={frac {1}{sqrt {5}}}left[varphi ^{n}-(1-varphi)^{n}right]}

for n 0 and n is a positive integer.

The golden ratio in geometry

The triangle of Kepler is a rectangle triangle formed by three squares with areas in geometric progression according to the golden number.

The golden ratio and the golden section are present in all regular or semi-regular geometric objects in which there is pentagonal symmetry, which are pentagons or where the square root of five appears in some way.

Relations between the Pentagon parts.
Relations between the parts of the starry pentagon, pentacle or staff.
Relations between the decagone parts.
Relations between the parts of the dodecahedron and the icosaedro.

Euclid's golden rectangle

The rectangle AEFD is golden because its sides AE and AD are in the proportion of the golden ratio. Euclid, in his proposition 2.11 of The elements , gets the construction of it:

GC={sqrt {5}}

With center in G we obtain the point E, and therefore:

GE=GC={sqrt {5}}

with which it is evident that

AE=AG+GE=1+{sqrt {5}}

from where, finally,

{frac {AE}{AD}}={frac {1+{sqrt {5}}}{2}}=varphi

On the other hand, the rectangles AEFD and BEFC are similar, so the latter is also a golden rectangle.

Generation of a golden rectangle from another

In another way:

{displaystyle varphi ={sqrt {left({frac {1}{2}}right)^{2}+1}}+{frac {1}{2}}}

On the staff

The coloured segments of the staff have golden proportions.

The golden ratio plays a very important role in regular pentagons and pentagrams. Each intersection of parts of a segment intersects another segment in a golden ratio.

The pentagram includes ten isosceles triangles: five acute and five obtuse. In both, the ratio of the longest side and the shortest side is φ. These triangles are known as the golden triangles.

Taking into account the great symmetry of this symbol, it is observed that within the inner pentagon it is possible to draw a new star, with a recursion to infinity. In the same way, it is possible to draw a pentagon on the outside, which would in turn be the inner pentagon of a larger star. When measuring the total length of one of the five lines of the inner pentacle, it is equal to the length of any of the arms of the major star, or Φ. Therefore, the number of times the golden ratio appears on the staff is infinite by adding infinitely many staves.

Ptolemy's theorem and the pentagon

You can calculate the golden number using the Ptolemy theorem in a regular pentagon.

Claudio Ptolemy developed a theorem known as Ptolemy's theorem, which allows us to draw a regular pentagon using a ruler and compass. Applying this theorem, a quadrilateral is formed by removing one of the vertices of the pentagon, If the diagonals and the larger base measure b, and the sides and the smaller base measure a, it turns out that b² = a² + ab which implies:

{displaystyle {b over a}={{1+{sqrt {5}}} over 2},.}

Starry Pentagon

The number of the right ratio between the partial segments of the sides of a stellated pentagon appears.

Trigonometry

The sine of 18º is half the inverse of the right ratio number.

cos 36 is half the golden number.

Similarly 2 cos 36o - 2 sen 18o = φ - 1/φ.

Relation to the Platonic solids

The golden ratio is related to the Platonic solids, in particular the icosahedron and the dodecahedron, whose dimensions are given in terms of the golden ratio.

The 12 vertices of an icosahedron with edges of length 2 can be expressed in Cartesian coordinates by the following points:

(0, ±1, ±φ), (±1, ±φ, 0), (±φ, 0, ±1)

The 20 vertices of a dodecahedron with edges of length 2/φ=√5−1 can also be given in similar terms:

(±1, ±1, ±1), (0, ±1/φ, ±φ), (±1/φ, ±φ, 0), (±φ, 0, ±1/φ)

The 12 vertices of the three golden rectangles match the centers of the faces of a dodecahedron.

For a dodecahedron with edges of length a, its volume and total area can also be expressed in terms of the golden ratio:

A=3{sqrt {15+20varphi }}cdot a^{2}

V={frac {4+7varphi }{2}}cdot a^{3}

If three golden rectangles overlap parallelly at their centers, the 12 vertices of the three golden rectangles coincide exactly with the vertices of an icosahedron, and with the centers of the faces of a dodecahedron.

The point that the rectangles have in common is the center of both the dodecahedron and the icosahedron.

The golden ratio in nature

Nautilus shell in logarithmic spiral

In nature, there are many elements related to the golden section and/or Fibonacci numbers:

Leonardo de Pisa (Fibonacci), in his Book of the Abbots (Liber abacci, 1202, 1228), uses the succession that takes its name to calculate the number of rabbit pairs n months after a first couple begins to reproduce (assuming that rabbits are isolated by walls, they begin to reproduce when they are two months old, they take one month from fertilization to childbirth and each bed is two rabbits). This is a purely independent mathematical problem that the involved are rabbits. In fact, the European common rabbit has 4 to 12 individual beds and several times a year, although not every month, despite the fact that pregnancies last 32 days. The problem is found in pages 123 and 124 of the 1228 manuscript, which was the one that came to us, and it seems that the approach resorted to rabbits as it might have been to other beings; it is a support to make understandable an unknown, a mathematical puzzle. The quotient of two consecutive terms of Fibonacci succession tends to the golden section or to the golden number if the resulting fraction is proper or improper, respectively. The same is true of any recurring succession of order two, as Barr and Schooling demonstrated in the magazine The Field December 14, 1912.

The disposition of the petals of the flowers (the role of the golden number in the botany receives the name of the Law of Ludwig).
The distribution of leaves in a stem. See: Fibonacci Succession.
The relationship between the nerves of the leaves of the trees.

The relationship between the thickness of the main branches and the trunk, or between the main branches and the secondary branches (the thickness of one equals Ω taking as unit the upper branch).
The amount of spirals of a pineapple (eight and thirteen spirals), flowers or inflorescences. These numbers are elements of the Fibonacci succession and the quotient of two consecutive elements tends to the golden number.
The distance between the navel and the sole of the feet of a person, regarding its total height.
The amount of petals in the flowers. There are flowers with 3, 5 and 8 petals and also with 13, 21, 34, 55, 89 and 144.
The distribution of the leaves of the yuca and the arrangement of the leaves of the alcachofas.
The relationship between the distance between the spiras of the spiral interior of any snail or cephalopods like nautilus. There are at least three logarithmic spirals more or less assimilable to aorean proportions. The first of them is characterized by the constant relationship equal to the golden number among the radiators of points located in two consecutive evoluts in the same direction and sense. The shells of the Fusus antiquusMurex, Scalaria pretiosaOf Facelaria and Solarium trochleareamong others, follow this type of growth spiral. It should be understood that in every natural consideration, although it involves the sciences considered more mathematically developed, such as Physics, no relationship or constant that has an infinite number of decimals can reach the mathematical limit, because on that scale there would be no physical object. The diminutive elementary particle you can imagine is infinitely larger than a point in a straight line. The laws observed and mathematically described in the organisms comply with them organically.
In order for the spread leaves of a plant (see Filotaxis) or branches around the trunk to have the maximum insolation with the minimum interference between them, they must grow separated in ascending helix according to a constant and theoretical angle equal to 360o (2 - φ) ≈ 137° 30' 27,950 580 136 276 726 855 462 662 132 999...". In nature a practical angle of 137o 30' or 137o 30' 28" will be measured at best. For the calculation it is considered vertical illumination and the mathematical criterion is that the horizontal projections of one another are not exactly recovered. Although the lighting of the Sun is not, in general, vertical and varies with latitude and seasons, this guarantees the maximum use of sunlight. This fact was empirically discovered by Church and mathematically confirmed by Weisner in 1875. In practice the angle cannot be measured so precisely and the plants reproduce it "organically"; that is, with a small deviation from the theoretical value. Not all plants benefit from a maximum of sun exposure or rain, so other constant angles differ from the ideal of 137.a 30'. You can find a table on page 26 of the full document accessible on the reference link.
In the amount of constituent elements of the spirals or double spirals of the inflorescences, as in the case of sunflower, and in other organic objects such as pineapples are numbers belonging to the succession of Fibonacci. The quotient of two successive numbers of this succession tends to the golden number.
There are pentagonal dodecaédrical pineapple crystals (piritoedros) whose faces are irregular pentagons. However, the proportions of such irregular polyhedron No. involve the golden number. In the inorganic world there is no regular pentagon. This appears (making the saving that with an organic error; we cannot pretend mathematical accuracy to the limit) exclusively in living organisms.

The golden ratio in art

Relations in the form of the Great Pyramid of Guiza. Herodoto's claim that the height square is equal to the surface of a face is possible only if the meridian semi-section of the pyramid is proportional to the rectangle triangle ${displaystyle textstyle left( 1.;{sqrt {frac {{sqrt {5}}+1}{2}}},;{frac {{sqrt {5}}+1}{2}}right)}$ , where 1 represents proportionally at the middle of the base, the square root of the golden number at the height to the vertex (not presently present) and the golden or hypotenuse number of the triangle to the apothesis of the Great Pyramid. This thesis has been defended by mathematicians Jarolimek, K. Kleppisch and W. A. Price (see references), is supported by the interpretation of a Herodoto passage (see references).History, book II, chap. 124) and is theoretically meaningful, although such a construction should contain inevitable errors to all architectural work and the very nature of human technology, which in practice can handle only rational numbers.

Other famous researchers favor the hypothesis that the builders intended to square the circle, since the square root of the golden ratio is very close to the ratio of 4 over π. But such a construction, even if π were known to a large approximation, would be entirely without geometric interest.

However, based on measurements it is not possible to choose between one or the other since the difference on the real monument is not greater than 14.2 cm and this small variation is masked by the uncertainties of the measurements, the construction errors and Mainly because the pyramid lost its coating in the hands of the first builders in Cairo. To make this clearer, a precision of 1 per thousand on a base of 230 meters is equivalent to 23 centimeters and in height it is in the order of the real difference that should exist between both possibilities.

The relationship between the parts, the ceiling and the columns of the Parthenon, in Athens (s. V a.C.). During the first quarter of the centuryXX.Jay Hambidge, from Yale University, was inspired by a passage from Plato Teeteto to study the relative proportions of the surfaces, something very natural when it comes to architectural works. Two non-similar rectangles are distinguished by the quotient of their main side by the minor, a number that is sufficient to characterize these figures and which called the rectangle module. One square has module 1 and the double square module 2. Those rectangles whose modules are whole or rational numbers were called "static" and those that possess euclidian irrational modules, that is, algebraicly express as roots of quadratic equations or reducible to them, "dynamic." The double square is both static and dynamic, as 2 is the square root of 4. An example of elemental dynamic rectangle is that which has on the main side the square root of 5 and on the lower side to the unit, being its module the square root of 5. Hambidge then studied Greek monuments and temples and came to frame the Parthenon's front in a module rectangle ${displaystyle {tfrac {4varphi -2}{varphi +1}}}$ . Through four diagonals it supplies the main vertical and horizontal proportions. This rectangle is broken into six modules ${sqrt {5}}$ and four squares.

As additional data to indicate the complexity of the treatment of the building, optical corrections were discovered in the Parthenon in 1837. The temple has three main views and if its columns were effectively plumb, all its lines were parallel and perfectly straight and the right angles were exact, due to the properties of human vision the whole would appear wider at the top than at the base, its Columns would be perceived as leaning outwards and the line that supports the roof on the columns would be seen as a kind of catenary, with the ends of the building appearing higher than the center. The builders made the construction compensating for these optical illusion effects by tilting or curving the elements involved in the opposite direction. Thus the outer columns, on both sides of the front, are inclined inward at an angle of 2.65 arc seconds, while those in the middle have an inclination of 2.61 arc seconds. The line that would form the lintels between columns and that constitutes the base of the triangle that crowns the building, is actually an angle of 2.64 seconds of arc with the vertex higher than the ends. In this way, and with other corrections that are not mentioned here, it is achieved that any observer who is located in the three main points of view sees the entire assembly parallel, uniform and straight.

Studies like Dr. Fechner have shown that the perception of beauty lies in the golden proportion. Therefore, what mathematically closest approaches to fi, will be perceived as more beautiful and perfect. This notion of beauty and perfection is applicable to architectural structures, paintings, musical scores, fractals and people.
In the table Atomic leda, by Salvador Dalí, done in collaboration with the Romanian mathematician Matila Ghyka.
In the structures and times of the films "The Potemkin Warehouse" and "Iván el Terrible" by Serguéi Eisenstein.
In the violins, the location of the ephes (the “hears” or holes in the lid) is related to the golden number.^{[chuckles]required]}
The golden number appears in the relations between height and width of objects and people that appear in the works of Michelangelo, Durero and Leonardo Da Vinci, among others.
It is necessary to deny the expanded assertion that the golden number appears in the well-known representation of the man of Vitruvio of Leonardo da Vinci. In this drawing Leonardo da Vinci strictly follows the fractional proportions of the human body that Vitruvio describes in his book De architectura; specifically in Chapter I of the Third Book, “The Origin of the Measures of the Temple”.
In the formal structures of Wolfgang Amadeus Mozart's sonatas, Fifth Symphony of Ludwig van Beethoven^{[chuckles]required]}in works by Franz Schubert^{[chuckles]required]} and Claude Debussy ^{[chuckles]required]} (these composers probably composed these relationships unconsciously, based on sound mass balances).
On the page. 56 of Dan Brown’s novel The code Da Vinci There is a messy version of the first eight Fibonacci numbers (13, 3, 2, 21, 1, 1, 8, 5), which work as a clue left by the Musée du Louvre, Jacques Saunière. In pp. 121-122 he explains some of the appearances of the number phi (1,618) in nature and the human being. It mentions that the distances between our body are proportional to each other, such as those from the leg to the thigh, the arm to the forearm, etc.
In the “Sabotage” episode of the television series NUMB3RS (first season, 2005), math genius Charlie Eppes mentions that the number fi is found in the structure of the crystals, in the spiral of the galaxies and in the shell of the Nautilus.
In the episode of Mentes Criminales "master's work" (Fourth season, episode 8), the crimes of Professor Rothschild follow a succession of Fibonacci; in the first area, he killed one victim; in the second, another; in the third, two; in the fourth, three; and in the fifth, five: twelve in total. Locations are also arranged according to a golden spiral, from outside to within: the place where children were kidnapped was right in the center. He even chose his first twelve victims as to how much the relationships between his facial features approached the golden number: he sought to be the "most perfect specimens of human beings."
The art Póvera was an Italian artistic movement of the 1960s, many of whose works are based on this succession.^{[chuckles]required]}
On the Darren Aronofsky tape Pi, faith in chaos/Pi, order of chaos, the central character, the mathematician Max Cohen, explains the relationship between the numbers of Fibonacci and the golden section, although denouncing it incorrectly Theta (θ) instead of Phi (Ω).
In Steel Ball Run, the seventh part of the popular JoJo's Bizarre Adventure sleeve franchise, the golden spiral is a crucial element within the plot, being the origin of the Spin technique used by the protagonists.
The phi number appears in the Disney movie Donald in the country of mathematics.

Contenido relacionado

Más resultados...