Gamma distribution

Density function of a Gamma.

In probability theory and statistics, the gamma distribution is a distribution with two parameters that belongs to the continuous probability distributions. The exponential distribution, the Erlang distribution, and the χ² distribution are particular cases of the gamma distribution. There are two different parameterizations that are commonly used

1. With shape parameter k{displaystyle k} and scale parameter θ θ {displaystyle theta }.
2. With shape parameter α α =k{displaystyle alpha =k} and reverse scale parameter λ λ =1/θ θ {displaystyle lambda =1/theta }.

Definition

Notation

If a continuous random variable X{displaystyle X} It has gamma distribution with parameters 0}" xmlns="http://www.w3.org/1998/Math/MathML">α α ▪0{displaystyle alpha 한0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/edd4f784b6e8bb68fa774213ceacbab2d97825dc" style="vertical-align: -0.338ex; width:5.749ex; height:2.176ex;"/> and 0}" xmlns="http://www.w3.org/1998/Math/MathML">λ λ ▪0{displaystyle lambda 한0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/eea25afc0351140f919cf791c49c1964b8b081de" style="vertical-align: -0.338ex; width:5.616ex; height:2.176ex;"/> Then we'll write X♥ ♥ Interpreter Interpreter (α α ,λ λ ){displaystyle Xsim Gamma (alphalambda)}.

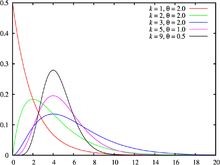
Density Function

Yeah. X♥ ♥ Interpreter Interpreter (α α ,λ λ ){displaystyle Xsim Gamma (alphalambda)} then its density function is

fX(x)=λ λ (λ λ x)α α − − 1e− − λ λ xInterpreter Interpreter (α α ){displaystyle f_{X}(x)={frac {lambda (lambda x)^{alpha -1}e^{-lambda x}{Gamma (alpha)}}}}}}}

for 0}" xmlns="http://www.w3.org/1998/Math/MathML">x▪0{displaystyle x 2005}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/> where

Interpreter Interpreter (α α )=∫ ∫ 0∞ ∞ tα α − − 1e− − tdt{displaystyle Gamma (alpha)=int _{0}^{infty }t^{alpha -1}e^{-t}dt}

is the gamma function and satisfies

1. Interpreter Interpreter (2)=Interpreter Interpreter (1)=1{displaystyle Gamma (2)=Gamma (1)=1}
2. For any 0}" xmlns="http://www.w3.org/1998/Math/MathML">α α ▪0{displaystyle alpha 한0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/edd4f784b6e8bb68fa774213ceacbab2d97825dc" style="vertical-align: -0.338ex; width:5.749ex; height:2.176ex;"/> is fulfilled Interpreter Interpreter (α α +1)=α α Interpreter Interpreter (α α ){displaystyle Gamma (alpha +1)=alpha Gamma (alpha)}
3. Yeah. n한 한 Z+{displaystyle nin mathbb {Z} ^{+} then. Interpreter Interpreter (n+1)=n!{displaystyle Gamma (n+1)=n!}
4. Interpreter Interpreter (12)=π π {displaystyle Gamma left({frac {1}{2}}{right)={sqrt {pi }}}}}
5. Yeah. n한 한 Z+{displaystyle nin mathbb {Z} ^{+} then. Interpreter Interpreter (n2)=π π (n− − 1)!2n− − 1(n− − 12)!{displaystyle Gamma left({frac {n}{2}}}right)={frac {{sqrt {pi }(n-1)}{2^{n-1}left({frac {n-1}{2}}{2}}}}}{2}}}}}}}}}}}

Cumulative Density Function

The accumulated distribution function of a random variable X♥ ♥ Interpreter Interpreter (α α ,λ λ ){displaystyle Xsim Gamma (alphalambda)} is given by

FX(x)=∫ ∫ 0xλ λ (λ λ and)α α − − 1e− − λ λ andInterpreter Interpreter (α α )dand{displaystyle F_{X}(x)=int _{0}^{x}{frac {lambda (lambda y)^{alpha-1}e^{-lambda y}}{Gamma (alpha)}}}}{;dy}

Yeah. X{displaystyle X} is a random variable such that X♥ ♥ Interpreter Interpreter (n,λ λ ){displaystyle Xsim Gamma (n,lambda)} where n한 한 Z+{displaystyle nin mathbb {Z} ^{+} (i.e., X{displaystyle X} has a distribution of Erlang) then its accumulated distribution function is given by

FX(x)=1− − ␡ ␡ k=0n− − 1(λ λ x)kk!e− − λ λ x=␡ ␡ k=n∞ ∞ (λ λ x)kk!e− − λ λ x{displaystyle {begin{aligned}F_{X}(x) fake=1-sum _{k=0}{n-1}{frac {(lambda x){k}{k}{k}{x}{k}{lambda x}{k}{k={infty }{

Properties

Yeah. X{displaystyle X} is a random variable such that X♥ ♥ Interpreter Interpreter (α α ,λ λ ){displaystyle Xsim Gamma (alphalambda)} then. X{displaystyle X} satisfies some properties.

Media

The mean of the random variable X{displaystyle X} That's it.

E[chuckles]X]=α α λ λ {displaystyle {text{E}}[X]={frac {alpha }{lambda }}}}}

Variance

Variance of the random variable X{displaystyle X} That's it.

Var[chuckles]X]=α α λ λ 2{displaystyle {text{Var}}[X]={frac {alpha }{lambda ^{2}}}}}}}}

Moments

The n{displaystyle n}-the moment of the random variable X{displaystyle X} That's it.

E [chuckles]Xn]=α α (α α +1) (α α +n− − 1)λ λ n{displaystyle operatorname {E} [X^{n}]={frac {alpha +1)cdots (alpha +n-1)}{lambda ^{n}}}}}}

for n한 한 N{displaystyle nin mathbb {N} }.

Moment generating function

The moment generating function is given by

MX(t)=(λ λ λ λ − − t)α α {displaystyle M_{X}(t)=left({frac {lambda }{lambda -t}right)^{alpha }}}

for t}" xmlns="http://www.w3.org/1998/Math/MathML">λ λ ▪t{displaystyle lambda t}t}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/06e1c46af304b4a4e76acd74280ba00c6709a2b3" style="vertical-align: -0.338ex; width:5.293ex; height:2.176ex;"/>.

Sum of Gammas

Yeah. Xi♥ ♥ Interpreter Interpreter (α α i,λ λ ){displaystyle X_{i}sim Gamma (alpha _{i},lambda)} for i=1,2,...... ,n{displaystyle i=1,2,dotsn} are independent random variables then

␡ ␡ i=1nXi♥ ♥ Interpreter Interpreter (␡ ␡ i=1nα α i,λ λ ){displaystyle sum _{i=1}^{n}X_{i}sim Gamma left(sum _{i=1}^{n}alpha _{i},lambda right)}

Scaling

Yeah. X♥ ♥ Interpreter Interpreter (α α ,λ λ ){displaystyle Xsim Gamma (alphalambda)} then for any 0}" xmlns="http://www.w3.org/1998/Math/MathML">c▪0{displaystyle c HCFC}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/2ba126f626d61752f62eaacaf11761a54de4dc84" style="vertical-align: -0.338ex; width:5.268ex; height:2.176ex;"/>

cX♥ ♥ Interpreter Interpreter (α α ,λ λ /c){displaystyle cXsim Gamma left(alphalambda /cright)}

Mean Logarithmic

It can be shown that

E [chuckles]ln (X)]=END END (α α )− − ln (λ λ ){displaystyle operatorname {E} [ln(X)]=psi (alpha)-ln(lambda)}

where END END {displaystyle psi } It's the digomma function.

Calculation of Probabilities in R

R (programme language) can be used to find density function values f(x){displaystyle f(x)} and distribution function F(x){displaystyle F(x)} of a continuous random variable X♥ ♥ Interpreter Interpreter (α α ,λ λ ){displaystyle Xsim Gamma (alphalambda)}.

Density function

Stop. 0}" xmlns="http://www.w3.org/1998/Math/MathML">x▪0{displaystyle x 2005}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>, the Gamma distribution density function is given by

fX(x)=λ λ (λ λ x)α α − − 1e− − λ λ xInterpreter Interpreter (α α ){displaystyle f_{X}(x)={frac {lambda (lambda x)^{alpha -1}e^{-lambda x}{Gamma (alpha)}}}}}}}

then to evaluate the density function f(x){displaystyle f(x)} We use the following code

# d=density functiondgamma(x,α,λ)

Distribution Function

The cdf of the gamma distribution is given by

FX(x)=∫ ∫ 0xλ λ (λ λ and)α α − − 1e− − λ λ andInterpreter Interpreter (α α )dand{displaystyle F_{X}(x)=int _{0}^{x}{frac {lambda (lambda y)^{alpha-1}e^{-lambda y}}{Gamma (alpha)}}}}{;dy}

for 0}" xmlns="http://www.w3.org/1998/Math/MathML">x▪0{displaystyle x 2005}0" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/80d24be5f0eb4a9173da6038badc8659546021d0" style="vertical-align: -0.338ex; width:5.591ex; height:2.176ex;"/>, you can use the following code to evaluate the accumulated distribution function F(x){displaystyle F(x)}

# p=probability distribution functionpgamma(x,α,λ)

Related Distributions

• Yeah. X1,X2,...... ,Xn{displaystyle X_{1},X_{2},dotsX_{n}} are independent and identically distributed random variables such that Xi♥ ♥ Exp(λ λ ){displaystyle X_{i}sim {text{Exp}}(lambda)} then. ␡ ␡ i=1nXi♥ ♥ Interpreter Interpreter (n,λ λ ){displaystyle sum limits _{i=1}^{n}X_{i}sim Gamma left(n,lambda right)}, this distribution is known as Erlang distribution and is a particular case of gamma distribution when the parameter α α =n한 한 N{displaystyle alpha =nin mathbb {N} }.

• Yeah. X♥ ♥ Interpreter Interpreter (1,λ λ ){displaystyle Xsim Gamma left(1,lambda right)} then. X♥ ♥ Exp(λ λ ){displaystyle Xsim {text{Exp}}(lambda)}.
• Yeah. X♥ ♥ Interpreter Interpreter (n2,12){displaystyle Xsim Gamma left({frac {n}{2}}},{frac {1}{2}}}right)} with n한 한 N{displaystyle nin mathbb {N} } then. X♥ ♥ χ χ n2{displaystyle Xsim chi _{n}^{2}}.