Games theory
Game theory is an area of applied mathematics that uses models to study interactions in formalized incentive structures (so-called «games»). Game theory has become an extremely important tool for economic science and has contributed to a better understanding of human behavior in decision-making. Its researchers study optimal strategies as well as the predicted and observed behavior of individuals in games. Apparently different types of interaction can actually present a similar incentive structure and, therefore, the same game can be represented a thousand times together.
Developed in its beginnings as a tool to understand the behavior of the economy, game theory has spread to many other fields, such as biology, computer science, sociology, political science, psychology and The philosophy. It experienced substantial growth and was first formalized from the work of John von Neumann and Oskar Morgenstern, before and during the Cold War, mainly due to its application to military strategy, particularly because of the concept of mutual destruction. guaranteed. Since the 1970s, game theory has been applied to animal behavior, including the development of species by natural selection. Following games like the prisoner's dilemma, in which pervasive egoism harms players, game theory has also attracted the attention of computer science researchers, being used in artificial intelligence and cybernetics.
Conflicts between rational beings who are suspicious of each other, or the struggle between competitors who interact and influence each other, who think and may even be capable of betraying each other, constitute the field of study of the theory. of games, which is based on a rigorous mathematical analysis but which, nevertheless, arises naturally when observing and analyzing a conflict from a rational point of view. From the perspective of this theory, a "game" is a conflictive situation in which conflicting interests of individuals or institutions take precedence, and in this context, one party, when making a decision, influences the decision that the other party will make; Thus, the outcome of the conflict is determined from all the decisions made by all the actors.
Game theory posits that there must be a rational way to play any "game" (or to negotiate in a conflict), especially when there are many tricky situations and ulterior motives; Thus, for example, the mutual anticipation of the opponent's intentions, which occurs in games such as chess or poker, gives rise to theoretically infinite chains of reasoning, which can also be transferred to the realm of real and complex conflict resolution. In summary, and as commented, individuals, when interacting in a conflict, will obtain results that are somehow totally dependent on such interaction.
Thus, since Von Neumann, Morgenstern and John Nash outlined the basic postulates of this theory during the 40s and 50s, there have been several applications that have been given to this tool in the field of economic decisions, Going so far as to modify the way in which economists interpreted decision-making and the achievement of the common good.
Game representation
Prisoner's Dilemma
One of the problems with Nash equilibrium is that it does not necessarily lead to efficient situations in the Pareto1 sense. The original analysis of this game is based on a situation in which two people who have jointly committed an armed robbery of a bank are interrogated in different rooms; however, the stolen money is not in their hands and, therefore, the police can only charge them with illegal possession of weapons, lacking other evidence. Thus, when interrogated separately, each of them would have the possibility of confessing guilt, implicating the other prisoner or denying having participated in the robbery. However, the police can offer them a deal and, through the use of an appropriate incentive scheme, make both confess to involvement in the act, get the truth out and convict them. Next, it will be seen that an adequate proposal made by the police force can lead to rationality and individual egoism with which decisions are usually made, which can turn against the joint interest of these subjects. To demonstrate this, consider, for example, the game called The Prisoner's Dilemma. This game allows you to understand that maintaining cooperation is extremely difficult. Many times individuals do not cooperate (this case is a paradoxical example, since it demonstrates the benefits that would be obtained by maintaining cooperation between any group of individuals, but at the same time it demonstrates that this, under certain postulates, is impossible to achieve), and their individual decisions do not necessarily lead to mutual well-being.
Normal form of a game
| Player 2 chooses left | Player 2 chooses right | |
|---|---|---|
| Player 1 chooses above | 4, 3 | -1, -1 |
| Player 1 chooses below | 0, 0 | 3, 4 |
The normal form (or strategic form) of a game is a payoff matrix, showing the players, strategies, and rewards (see the example on the right). There are two types of players; one chooses the row and another the column. Each player has two strategies, which are specified by the number of rows and the number of columns. The rewards are specified inside. The first number is the reward received by the player in the ranks (Player 1 in our example); the second is the reward of the player in the columns (the Player 2 in our example). If player 1 chooses up and player 2 chooses left then their rewards are 4 and 3, respectively.
When a game is presented in normal form, it is assumed that all players act simultaneously or, at least, without knowing the choice that the other is making. If the players have any information about other players' choices, the game is usually presented in the extensive form.
There is also a reduced normal form. It combines strategies associated with the same payment.
Extensive form of a game
The extensive form representation of games models games with some order to be considered. The games are presented as trees (as shown on the right). Each vertex or node represents a point where the player makes decisions. The player is specified by a number next to the vertex. The lines that start from the vertex represent possible actions for the player. The rewards are specified on the leaves of the tree.
In the game shown in the example there are two players. Player 1 moves first and chooses F or U. Player 2 sees Player 1's move and chooses A or R. If player 1 chooses U and then player 2 chooses A, then player 1 gets 8 and player 2 gets 2.
Games in extensive form can also model simultaneous move games. In such cases, a dotted line or a circle is drawn around two different vertices to represent them as part of the same information set (for example, when the players do not know where they are).
Normal form gives the mathematician a simple notation for the study of equilibrium problems, because it dismisses the question of how strategies are calculated or, in other words, how the game is actually played. The convenient notation for dealing with these issues, most relevant to combinatorial game theory, is the extensive form of the game.
Types of games and examples
The theory classifies games into many categories that determine what particular methods can be applied to solve them (and, indeed, also how "solving" is defined in a particular category). Common categories include:
Symmetrical and asymmetrical games
| E | F | |
|---|---|---|
| E | 1, 2 | 0, 0 |
| F | 0, 0 | 1, 2 |
A symmetrical game is a game in which the rewards for playing a particular strategy depend only on the strategies used by the other players and not on who plays them. If the identities of the players can be changed without the payoffs of the strategies changing, then the game is symmetric. Many of the most studied 2×2 games are symmetrical. The standard representations of the game of chicken, the prisoner's dilemma, and the stag hunt are symmetrical games.
The most studied asymmetric games are the games where there are no identical strategy sets for both players. For example, the Ultimatum Game and the Dictator Game have different strategies for each player; however, there can be asymmetric games with identical strategies for each player. For example, the game shown on the right is asymmetric despite having identical strategy sets for both players.
Zero-Sum and Non-Zero-Sum Games
| A | B | C | |
|---|---|---|---|
| 1 | 30, -30 | -10, 10 | 20, -20 |
| 2 | 10, -10 | 20, -20 | - 30, 30 |
In zero-sum games the total payoff to all players in the game, in each combination of strategies, always adds up to zero (in other words, one player benefits only at the expense of others).. Go, chess, poker, and the bear game are examples of zero-sum games, because you win exactly the amount your opponent loses. As a curiosity, soccer stopped being zero-sum a few years ago, since victories reported 2 points and a tie 1 (consider that both teams initially start with 1 point), while currently victories report 3 points and a draw 1.
Most real-world examples in business and politics, like the prisoner's dilemma, are nonzero-sum games, because some outcomes have net outcomes greater than or less than zero. That is, the gain of one player does not necessarily correspond to the loss of another. For example, a business contract ideally involves a positive-sum outcome, where each opponent ends up in a better position than he or she would have if the negotiation had not taken place.
A non-zero sum game can be more easily analyzed, and any game can be turned into a zero sum game by adding a "dummy" ("the board" or "the bank"), whose losses offset the net gains of the players.
The payoff matrix of a game is a convenient form of representation. For example, a two-player zero-sum game with the matrix shown to the right.
"Maximin" and "minimax" criteria
The “maximin” and “minimax” criteria state that each player must minimize his maximum loss:
- Criterion "maximin": Player A, chooses that its minimum charge is the greatest.
- Criterion "minimax": player B chooses that the maximum payment to A is the least possible.
Nash equilibrium
Dominance strategy equilibria are all very well when they appear in games, but unfortunately, that doesn't happen often.
A pair of strategies is a Nash equilibrium if player A's choice is optimal, given B's choice, and B's is optimal, given A's.
Nash equilibrium can be interpreted as a pair of expectations about each person's choice such that, when the other reveals their choice, neither wants to change their behavior.
Each player knows and has adopted his best strategy, and everyone knows each other's strategies. Consequently, each individual player gains nothing by changing his strategy as long as the others stick to theirs. Thus, each player is executing the best "move" that can given the moves of the other players.
Cooperative games
A cooperative game is characterized by a contract that can be enforced. Cooperative game theory gives plausible contract justifications. The plausibility of a contract is closely related to stability.
Two players negotiate so much they want to invest in a contract. The axiomatic trading theory shows us how much investment is convenient for us. For example, the Nash solution to bargaining demands that investment be fair and efficient.
Either way, we might not be interested in justice and demand more. In fact, there is a non-cooperative game created by Ariel Rubinstein consisting of alternating offers, which supports the Nash solution, considering it the best, through the so-called Nash equilibrium. Cooperative play in Mathematics time
In this sense, we propose to analyze didactic sequences so that our students “do math”, that is, explore, establish relationships, confront their productions with those of others, discuss with their peers, make decisions, argue, validate propositions, produce knowledge. so that this work Whenever possible, it is necessary to pose problems that imply a certain level of challenge; a fertile context for posing these challenges is that of games.
Simultaneous and sequential
Simultaneous games are games in which players move simultaneously or are unaware of other players' previous moves. Sequential (or dynamic) games are games in which subsequent players have some knowledge of previous actions. This knowledge does not necessarily have to be perfect; it should only consist of some information. For example, player1 may know that player2 did not perform a certain action, but not know which of the other available actions he chose.
The difference between simultaneous and sequential games is captured in the representations discussed previously. The normal form is used to represent simultaneous games, and the extensive form to represent sequential games.
Perfect Information Games
An important subset of sequential games is the set of perfect information games. A game is of perfect information if all the players know the moves that all the other players have previously made; so only sequential games can be games of perfect information, since in simultaneous games not all players (often none) know the actions of the rest. Most of the games studied in game theory are imperfect information games, although some interesting games are perfect information games, including the ultimatum game and the centipede game. Also many popular games are information perfect, including chess and go.
Perfect information is often confused with complete information, which is a similar concept. Complete information requires each player to know the strategies and rewards of the rest but not necessarily the actions.
In full information games each player has the same "game-relevant information" than the other players. Chess and the prisoner's dilemma exemplify complete information games. Full information games rarely occur in the real world, and game theorists usually see them only as approximations of the game actually played.
The English mathematician and Princeton University Professor Emeritus John Conway developed a notation for some complete information games and defined various operations on those games, originally to study the endings of go, although much of this analysis focused on nim. This became combinatory game theory.
Conway discovered that there is a subclass of those games that can be used as numbers, as he described in his book On Numbers and Games (1976), leading to the very general class of surreal numbers.
Games of infinite length
For obvious reasons, the games studied by economists and the games in the real world generally end after a finite number of moves. Pure mathematical games do not have these restrictions and set theory studies games of infinite moves, where the winner is not known until all moves are known.
The interest in such a situation is usually not in deciding the best way to play a game, but simply in which player has a winning strategy (It can be proved, using the axiom of choice, that there are games—even of perfect information, and where the only rewards are 'losing' and 'winning'—for which no player has a winning strategy.) The existence of such strategies has consequences important in descriptive set theory.
Combination Games
Games in which the difficulty of finding an optimal strategy comes from the multiplicity of possible moves are called combinatorial games. Some examples of these games can be chess and go. Games that involve imperfect or incomplete information can also have a strong combinatory character, for example backgammon. There is no unified theory that deals with combinatorial elements in games. There are, however, mathematical tools that can solve particular problems and answer general questions.
Games of perfect information have been studied in combinatorial game theory, which has developed new representations such as surreal numbers, as well as combinatorial and algebraic (and sometimes non-constructive) proof methods for solving games of certain types, including "loopy" that can give rise to infinitely long sequences of movements. These methods address games with greater combinatorial complexity than those normally considered in traditional (or "economic") game theory. A typical game that has been solved in this way is hexadecimal. A related field of study, based on computational complexity theory, is game complexity, which is concerned with estimating the computational difficulty of finding optimal strategies.
Research in artificial intelligence has addressed perfect and imperfect (or incomplete) information games that have very complex combinatorial structures (such as chess, go, or backgammon) for which no verifiable optimal strategies have been found. Practical solutions involve computational heuristics, such as alpha-beta pruning or the use of artificial neural networks trained by reinforcement learning, which make games more manageable in practical computing.
Continuous play
Much of game theory is concerned with finite, discrete games, which have a finite number of players, moves, events, outcomes, etc. However, many concepts can be extended. Continuous games allow players to choose one strategy from a set of continuous strategies. For example, Cournot competition is typically modeled with the strategies of players for any non-negative amounts, including fractional amounts.
Differential games
Differential games are continuous games where the evolution of the players' state variables is governed by differential equations. The problem of finding an optimal strategy in a differential game is closely related to the theory of optimal control. In particular, there are two types of strategies: open-loop strategies use the maximum Pontryagin principle, while closed-loop strategies use Bellman's dynamic programming method.
A particular case of differential games are games with a random time horizon. In these games, the terminal time is a random variable with a given probability distribution function. Therefore, players maximize the mathematical expectation of the cost function. It was shown that the modified optimization problem can be reformulated as a differential game with discount on an infinite time interval.
Games with many players and populations
Games with an arbitrary, but finite, number of players are often called n-person games. Evolutionary game theory considers games involving a population of decision makers, where the frequency with which a particular decision is made may change over time in response to decisions made by all individuals in the population. In biology, this is used to model (biological) evolution, where genetically programmed organisms pass along some of their programming strategy to their offspring. In economics, the same theory is meant to capture population changes because people play the game many times within their lifetime, and consciously (and perhaps rationally) change strategies.
Stochastic results (and relation to other fields)
Individual decision problems with stochastic outcomes are sometimes considered "single player games". These situations are not considered game theoretical by some authors. They can be modeled using similar tools within the related disciplines of decision theory, operations research, and areas of artificial intelligence, particularly AI planning (with uncertainty) and multi-agent systems. Although these fields may have different drivers, the mathematics involved are substantially the same, for example using Markov Decision Processes (MDPs). Stochastic outcomes can also be modeled in game-theoretic terms by adding a random action player making "chance moves" ("moves by nature"). This player is not usually considered a third player in what is otherwise a two-player game, but simply serves to provide a die roll when required by the player. game.
For some problems, different approaches to modeling stochastic results may lead to different solutions. For example, the difference in approach between MDPs and the minimax solution is that the latter considers the worst case on a set of adversary moves, instead of reasoning on the expectation of these moves given a fixed probability distribution. The minimax approach may be advantageous when stochastic models of uncertainty are not available, but it may also be overestimating extremely unlikely (but costly) events, dramatically changing strategy in such scenarios if it is assumed that an adversary can force such an event to happen. General models including all elements of stochastic outcomes, adversaries, and partial or noisy observability (of other players' moves) have also been studied. The "gold standard" is a partially observable stochastic game (POSG), but few realistic problems are computationally feasible in the POSG representation.
Metagames
These are games where you try to develop the rules for another game, the target, or the player. Metagames seek to maximize the utility value of the developed ruleset. Metagame theory is related to mechanism design theory.
The term metagame analysis is also used to refer to a practical approach developed by Nigel Howard. Therefore, a situation is framed as a strategic game in which the interested parties try to achieve their objectives through the available options. Subsequent events have led to the formulation of confrontation analysis.
Applications
Game theory has the characteristic of being an area in which the underlying substance is primarily a category of applied mathematics, but most fundamental research is carried out by specialists in other areas. In some universities it is taught and researched almost exclusively outside of the mathematics department.
This theory has applications in many areas, including economics, evolutionary biology, psychology, political science, industrial design, operations research, computer science, and military strategy.
Economy and business
Economists have used game theory to analyze a wide range of economic problems, including auctions, duopolies, oligopolies, the formation of social networks, and voting systems. These investigations are usually focused on particular sets of strategies known as solution concepts. These solution concepts are normally based on what is required by the rules of perfect rationality. The most famous is the Nash equilibrium. A set of strategies is a Nash equilibrium if each represents the best response to other strategies. In this way, if all the players are applying the strategies in a Nash equilibrium, they have no incentive to change their behavior, since their strategy is the best that they can apply given the strategies of the others.
Game rewards typically represent the utility of individual players. Rewards often represent money, which is presumed to correspond to an individual's utility. This assumption, however, may not be correct.
A game theory paper in economics begins by presenting a game that is an abstraction of a particular economic situation. One or more solutions are chosen, and the author shows which set of strategies correspond to the equilibrium in the presented game. Economists and business school professors suggest two main uses.
Descriptive
The main use is to inform about the behavior of current human populations. Some researchers believe that finding the equilibrium of the games can predict how human populations would behave if faced with situations analogous to the game studied. This particular view of game theory has been criticized today. First, it is criticized because the assumptions of theorists are frequently violated. Game theorists may assume players always behave rationally and act to maximize profit (the Homo oeconomicus model), but real humans often act irrationally or rationally but for the benefit of a larger group (altruism).
Game theorists respond by comparing their assumptions to those used in physics. Thus, although their assumptions do not always hold, they can treat game theory as a reasonable idealization, in the same way as the models used by physicists. However, this use of game theory has continued to be criticized because some experiments have shown that individuals do not behave according to equilibrium strategies. For example, in the centipede game, the ⅔-of-the-mean guessing game, and the dictator game, people often do not behave according to Nash equilibrium. This controversy is currently being resolved.
On the other hand, some authors argue that Nash equilibria do not provide predictions for human populations, but rather provide an explanation of why populations that behave according to Nash equilibrium remain in that behavior. However, the question of how many people behave this way remains open.
Some game theorists have pinned hopes on evolutionary game theory to resolve these concerns. Such models presuppose either no rationality or a bounded rationality in the players. Despite the name, evolutionary game theory does not necessarily presuppose natural selection in the biological sense. Evolutionary game theory includes biological and cultural evolution and also models individual learning.
Regulations
| Cooperate | Trace | |
|---|---|---|
| Cooperate | 2 2 | 0 3 |
| Trace | 3 0 | 1 1 |
On the other hand, some mathematicians do not see game theory as a tool that predicts the behavior of human beings, but as a suggestion about how they should behave. Since the Nash equilibrium is the best response to the actions of other players, following a strategy that is part of the Nash equilibrium seems most appropriate. However, this use of game theory has also received criticism. First, in some cases it is appropriate to play a non-equilibrium strategy if one expects that others will also play according to equilibrium. For example, in the game guess ⅔ of the mean.
The prisoner's dilemma presents another potential counterexample. In this game, if each player pursues his own benefit, both players get a worse result than if they had not. Some mathematicians believe that this demonstrates the failure of game theory as a course recommendation.
Psychology and psychiatry
Experimental designs based on games of economic exchange have begun to be used for the study of people with psychiatric disorders and the understanding of the neural functioning that underlies cognitive processes and affective processing; emphasizing decision-making between two or more people in the face of the possibility of distributing economic goods In this sense, it is known that people make decisions in economic games according to their ability to experience trust, as well as their implicit and explicit processing of the trustworthiness of their peers.
Biology
| Falcon | Paloma | |
|---|---|---|
| Falcon | (V-C)/2 (V-C)/2 | V 0 |
| Paloma | 0 V | V/2 V/2 |
Unlike the use of game theory in economics, the rewards of games in biology are frequently interpreted as adaptation. In addition, his study has focused less on the balance that corresponds to the notion of rationality, focusing on the balance maintained by evolutionary forces. The best known equilibrium in biology is known as an evolutionarily stable strategy, and it was first introduced by John Maynard Smith. Although his initial motivation did not carry the mental requirements of Nash equilibrium, every evolutionarily stable strategy is a Nash equilibrium.
In biology, game theory is used to understand many different problems. It was first used to explain the evolution (and stability) of 1:1 sex ratios (same number of males as females). Ronald Fisher suggested in 1930 that the 1:1 ratio is the result of individuals trying to maximize the number of their grandchildren subject to the constraints of evolutionary forces.
It should be noted that biologists have used evolutionary game theory and the concept of evolutionarily stable strategy to explain the emergence of animal communication (John Maynard Smith and Harper in 2003). Analysis of signaling and other communication games has provided new insights into the evolution of communication in animals.
Finally, biologists have used the hawk-dove problem (also known as the chicken problem) to analyze combative behavior and territoriality.
Computer science and logic
Game theory has begun to play an important role in logic and computer science. Many logical theories are based on game semantics. In addition, computer researchers have used games to model programs that interact with each other.
Political Science
Political science research has also used results from game theory. One explanation of democratic peace theory is that open public debate in democracy sends clear and reliable information about the intentions of governments towards other states. On the other hand, it is difficult to know the interests of non-democratic leaders, what privileges they will grant and what promises they will keep. According to this reasoning, there will be mistrust and little cooperation if at least one party to a dispute is not a democracy.
The application of game theory in political science extends into other areas such as fair division, economic policy, public decisions, war negotiations, positive political theory, and social choice theory. In each of these areas, researchers have developed game-theoretic models in which the players are voters, states, interest groups or bureaucrats, and politicians.
Some of these game theory examples were explained by Anthony Downs. In his book An Economic Theory of Democracy , in which he applied Hotelling's Law to the political process. In the Downsian model, political candidates perpetrate ideologies in a space with a political dimension. Downs first shows how political candidates will converge to the preferred ideology of the median voter if voters are fully informed. But then, he argues, voters choose to remain rational by ignoring what allows for candidate divergence to take place. Also, it was applied in 1962 in the Cuban missile crisis during John's presidency. F.Kennedy.
Criminal Law and Criminology
Recently, the usefulness of game theory and its analysis methodologies is being addressed to support the criminal liability of legal persons (companies, associations, foundations, etc.) and for the development of prediction, detection and reaction to crimes committed by managers and employees in this type of organization. The Spanish jurist Rafael Aguilera has been a pioneer in this line of research by proposing in his studies the use of game theory and socioeconomic theories in corporate Criminal Law and Criminology, specifically for:
a) Establish an anthropic model of criminal liability of legal entities.
In this representation, the corporate entity is not a true entity, independent and with the capacity to direct itself, but is configured by the points (which are the individuals of the organization) and the constraints, limitations and procedures (represented by lines). which, strictly speaking, are decided and configured by the individuals themselves. The legal person does not have the capacity to commit an injustice or guilt, but the responsibility is transferred to it, after analyzing the constraints. The entity is conceived as a possible recipient of criminal responsibility due to the «visibility» it holds by virtue of the constraints and the individuals themselves who originate and implement them. If, as a result of an individual's criminal conduct, the inexistence of some constraints and procedures tending to prevent crimes is observed or they are observed to be defective or favoring the commission of illicit acts (represented by red lines), a deficit is being observed. organizational, an aspect implicit in the "fact of connection" and this leads to the transfer of criminal responsibility to the legal entity.
Anthropic model of corporate criminal responsibility of Aguilera.
b) The development of crime prevention programs or corporate compliance programs that enable a more effective response to crime in the company.
Aguilera addresses the extraordinary utility of game theory for the legal-criminal and business criminology fields, since it allows a rigorous study of the dynamics of action and the interaction of a strategic nature between participants who act directed by their own interests. Game theory makes it possible to explain how individuals, through their rational behavior and based on interactions with others, regulate themselves or adopt certain decisions. In addition, game theory is accompanied by a valuable methodological development that enables the analysis of decision-making processes, taking into account such important elements to analyze and elucidate criminal responsibilities, such as information asymmetries and compliance or non-compliance with the rules for strategic reasons (such as occurs, for example, in the famous Prisoner's Dilemma).
Similarly, Aguilera argues why the States are promoting, through the possibility of exemption from corporate criminal liability, the incorporation of the figure of the compliance officer or compliance officer and is that this theory mathematically demonstrates that the compliance officer reduces the tendency of companies or other organizations to default (what is known in game theory as external solution to the dilemma).
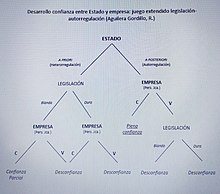
This author argues that game theory is fully acceptable and extraordinarily useful for developing more effective crime prevention programs or corporate compliance programs, since they make it possible to predict illegal behavior by taking into account aspects such as information flows, interpersonal relationships, tactical aspects with respect to other individuals or groups of individuals, as well as the influence exerted by organizations; risks are analyzed from a dynamic and live perspective, as is the business reality itself and not from the usual static perspective (which is how it has traditionally been done through the use of classic risk matrices).
The result of using game theory in the business context is obtaining a greater clarification of the wide range of behaviors that each worker can carry out according to the position he occupies, not in an isolated and static way, but taking into account that the decision of each employee depends, in turn, on the decisions of other employees -strategic decisions in dynamic environments-. In this way, it can be solved, for example, how an employee who deals with the accounting of a company or another whose function is to sign purchase contracts with third parties would act; Based on this global information that takes into account all the strategic factors (according to a scientifically proven methodology), unique procedures can be established that “force” each member of the company to act in one way or another depending on the subjects that intervened., specific circumstances and context to respect the legal framework. The application of game theory in the development of crime prevention programs together with jurimetry makes it possible to obtain what Aguilera calls a model of organization and management or legal compliance. In other words, the author defends that the use of modeling to develop more effective compliance to combat crimes in companies.
In addition, the use of this methodology to develop a corporate compliance program or crime prevention program shows that, in the organization, there is a firm commitment to crime prevention and regulatory compliance, which multiplies the options for exclusion or release of criminal liability to the legal person itself when one of its members managed to commit a crime.
On the other hand, the author relates the usefulness of game theory to the current boom in computer programs and tools for risk, cost, and benefit analysis in business decision-making processes. These programs make use of a huge amount of data and perform millions of mathematical operations taking into account the set of possible decisions, all their consequences and the list of strategies to be adopted; its results yield very precious information, for example, which is the decision that carries the most danger, which is the most conservative, the most expensive, etc. At the end of the day, it is about the translation into computer language of mathematical models and methodology that come from the economic theories themselves, game theory or the new institutionalism of rational choice. That is to say, from computer science it has also been assuming the validity and usefulness of the aforementioned theories when it comes to analyzing and predicting behaviors of individuals in organizations. However, this link between both areas is not contemplated from the legal-criminal level. In this regard, he proposes a determined assimilation by Criminal Law of the proposals developed in the investigation would allow the establishment of what Aguilera comes to call logical nexus of socio-legal roots, which would make it possible to address with greater solvency the difficulties, legal challenges and ethical dilemmas that the use of these new computer tools by companies poses and will pose.
Philosophy
Game theory has proven to have many uses in philosophy. Building on two works by W. V. O. Quine published in 1960 and 1967, David Lewis (1969) used game theory to develop the philosophical concept of convention. In this way, he provided the first analysis of common knowledge and used it to analyze coordination games. Furthermore, he was the first to suggest that meaning could be understood in terms of signal plays. This suggestion has been followed by many philosophers since Lewis's work.
Leon Henkin, Paul Lorenzen, and Jaakko Hintikka initiated an approach to the semantics of formal languages that explains with game-theoretic concepts the concepts of logical truth, validity, and the like. In this approach the "players" they compete by proposing quantifications and instances of open sentences; the rules of the game are the rules of interpretation of the sentences in a model, and the strategies of each player have properties that semantic theory deals with (being dominant if and only if the sentences that are played with meet certain conditions, etc.).
| Deer | Hare | |
|---|---|---|
| Deer | 3, 3 | 0, 2 |
| Hare | 2, 0 | 2, 2 |
In ethics, some authors have attempted to continue Thomas Hobbes's idea of deriving morality from personal interest. Since games like Prisoner's Dilemma present an apparent conflict between morality and self-interest, explaining why cooperation is necessary for self-interest is an important component of this project. This general strategy is a component of the idea of the social contract in political philosophy (examples in Gauthier 1987 and Kavka 1986).
Finally, other authors have attempted to use evolutionary game theory to explain the birth of human attitudes toward morality and corresponding animal behaviors. These authors have searched for examples in many games, including the prisoner's dilemma, the stag hunt, and the Nash bargain game to explain the reason for the emergence of attitudes about morality (see Skyrms 1996, 2004; Sober and Wilson 1999).
Music
A composer who uses game theory in his compositions is Iannis Xenakis, in his works Duel or Stratégie.
Design optimization
The theory of design optimization dictates five characteristic principles of a game, without which it would cease to be called in such a way:
- Rules: They must be easy to understand, but only through the experience to be completely dominated.
- Interaction (Participation): Players, through the intervention of the created world, must forget the real world.
- Opposition: The game must be balanced. Skill is required to win, not luck.
- Decision-making: All decision-making must have an inciteer of interest and merit as small as possible.
- Target: A final point to reach. It must be accompanied by an increase in emotions and tension while the game approaches its conclusion.
History of Game Theory
| Year | Development |
|---|---|
| 1713 | James Waldegrave gives the first mathematical demonstration for a case of two players. |
| 1838 | Antoine Augustin Cournot publishes a theoretical solution case of two players. |
| 1928 | John von Neumann presents a series of articles on the subject. |
| 1944 | John von Neumann along with Oskar Morgenstern publish Theory of Games and Economic Behavior. |
| 1950 | Albert W. Tucker formally raised "the prisoner's dilemma," fundamental in the theory of games. John Forbes Nash, under the direction of Albert W. Tucker, is a doctor with a thesis on non-cooperative games, which includes what was later called the balance of Nash. |
| 1965 | Reinhard Selten introduced his concept of balancing perfect of the subgame, which later refined the balance of Nash. |
| 1967 | John Harsanyi developed the concepts of information Complete and Berriesian games. |
| 1982 | In biology John Maynard Smith introduces the concept of Evolutionaryly stable strategy. |
| 1994 | John Harsanyi, John Forbes Nash and Reinhard Selten they win the Prize in Economics in memory of Alfred Nobel. |
| 2012 | Lloyd Stowell Shapley and Alvin E. Roth they win the Prize in Economics in memory of Alfred Nobel. |
The first known discussion of game theory appears in a letter written by James Waldegrave in 1713. In this letter, Waldegrave provides a minimal mixed-strategy solution to a two-person version of the card game le Her. However, a theoretical analysis of game theory in general was not published until the publication of Recherches sur les príncipes mathématiques de la théorie des richesses, by Antoine Augustin Cournot in 1838. In this work, Cournot considers a duopoly and presents a solution that is a restricted version of the Nash equilibrium.
Although Cournot's analysis is more general than Waldegrave's, game theory did not really exist as a separate field of study until John von Neumann published a series of papers in 1928. These results were later expanded upon in his book 1944, Theory of Games and Economic Behavior, co-authored with Oskar Morgenstern. This work contains a method to find optimal solutions for two-person zero-sum games. During this period, work on game theory focused primarily on cooperative game theory. This type of game theory analyzes the optimal strategies for groups of individuals, assuming that they can agree among themselves about the most appropriate strategies.
In 1950 Albert W. Tucker formally raised the first discussions of the prisoner's dilemma, and an experiment on this game was undertaken at the RAND corporation. In that year John Nash developed a definition of an optimal strategy for multiplayer games where the optimum had not been previously defined, known as Nash equilibrium, under the supervision of the aforementioned Tucker. This equilibrium is general enough to allow the analysis of non-cooperative games in addition to cooperative games.
Game theory experienced a remarkable activity in the 1950s, at which time the basic concepts, the extensive form game, the fictional game, repetitive games, and the Shapley value were developed. Also, at that time, the first applications of game theory appeared in philosophy and political science.
In 1965, Reinhard Selten introduced his concept of solving subgame perfect equilibria and the concept of shaky-hand perfect equilibrium, which further refined the concept of Nash equilibrium. In 1967 John Harsanyi developed the concepts of complete information and Bayesian games. He, along with John Forbes Nash and Reinhard Selten, won the Alfred Nobel Memorial Prize in Economic Sciences in 1994.
In the 1970s game theory was widely applied to biology, largely as a result of the work of John Maynard Smith and his concept of evolutionary stable strategy. In addition, the concepts of correlated balance, perfect shaky hand balance, and common knowledge were introduced and discussed.
In 2005, game theorists Thomas Schelling and Robert Aumann won the Alfred Nobel Memorial Prize in Economic Sciences. Schelling worked on dynamic models, the first examples of evolutionary game theory. For his part, Aumann contributed more to the school of equilibrium.
In 2007, Roger Myerson, along with Leonid Hurwicz and Eric Maskin, received the Alfred Nobel Memorial Prize in Economic Sciences for "laying the foundations of mechanism design theory."
In 2012, Lloyd Stowell Shapley and Alvin E. Roth won the Alfred Nobel Memorial Prize in Economic Sciences for naming half a dozen theorems, algorithms, principles, solutions, and indices in the field.
Contenido relacionado
Gene
Imaginary number
Dactyloctenium


