Friendly numbers

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Demonstration with stripes that (220 and 284) are numbers friends

Two different natural numbers related in such a way that the sum of the proper divisors of each one is equal to the other number are called friendly numbers. That is, σ(a)=b and σ(b)=a, where σ(n) is equal to the sum of the proper divisors of n (see also the divisor function).

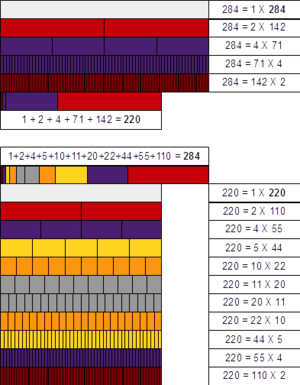
The smallest pair of friendly numbers is (220, 284), and they are friends because the proper divisors of 220 are 1, 2, 4, 5, 10, 11, 20, 22, 44, 55, and 110, of of which the sum is 284; and the proper divisors of 284 are 1, 2, 4, 71, and 142, of which the sum is 220 (a proper divisor of a number is a positive factor of that number other than the number itself. For example, the proper divisors proper of 6 are 1, 2 and 3, but not 6).

The first ten pairs of friendly numbers are: (220, 284), (1184, 1210), (2620, 2924), (5020, 5564), (6232, 6368), (10744, 10856), (12285, 14595), (17296, 18416), (63020, 76084) and (66928, 66992). (sequence A259180 in OEIS) (see also (sequence A002025 in OEIS) and (sequence A002046 in OEIS)) It is unknown if there are infinitely many pairs of friendly numbers.

A pair of friendly numbers constitutes an aliquot sequence of period 2. A related concept is that of a perfect number, which is a number that is equal to the sum of "its" proper divisors, in other words, a number that forms an aliquot sequence of period 1. Numbers that are members of an aliquot sequence with period greater than 2 are known as sociable numbers.

History

Unresolved problems of mathematics: Are there infinite couples of friends numbers?

Friendly numbers were known to the Pythagoreans, who attributed many mystical properties to them. The Iraqi mathematician Thábit ibn Qurra (826–901) invented a general formula by which some of these numbers could be found around the year 850. Other Arab mathematicians who studied friendly numbers included al-Majriti (died 1007), al- Baghdadi (980–1037) and al-Fārisī (1260–1320). The Iranian mathematician Muhammad Baqir Yazdi (16th century) discovered the pair (9363584, 9437056), although this achievement has often been attributed to Descartes. Much of the work of Islamic mathematics in this area has been forgotten.

Thābit ibn Qurra's formula was rediscovered by Fermat (1601–1665) and Descartes (1596–1650), to whom it is sometimes attributed, and extended by Euler (1707–1783). It was further extended by Borho in 1972. Fermat and Descartes also rediscovered pairs of friendly numbers known to Arab mathematicians. Euler also discovered dozens of new pairs. The second smallest pair, (1184, 1210), was discovered in 1867 by 16-year-old B. Nicolò I. Paganini (not to be confused with the composer and violinist), after been overlooked by earlier mathematicians.

The first ten pairs of friends numbers
#	m	n
1	220	284
2	1184	1210
3	2620	2924
4	5020	5564
5	6232	6368
6	10 744	10 856
7	12 285	14 595
8	17 296	18 416
9	63 020	76 084
10	66 928	66 992

By 1946 there were 390 known pairs, but the advent of computers has allowed the discovery of many thousands since then. Extensive searches have been performed to find all pairs below a given limit, extending this limit from 10⁸ in 1970, to 10¹⁰ in 1986, 10¹¹ in 1993, 10¹⁷ in 2015 and up to 10¹⁸ in 2016.

As of 2022 out of 10, there are more than 1,227,366,104 known pairs of friendly numbers.

Rules for generation

Although these rules generate some pairs of friendly numbers, many other pairs are known, so these rules are not exhaustive.

In particular, the two rules below yield only even friendly pairs, so they are not relevant to the open problem of finding coprime friendly pairs a 210 = 2 3 5 7, while known more than 1000 coprime pairs at 30 = 2·3·5 [García, Pedersen & te Riele (2003), Sándor & Crstici (2004)].

Thābit ibn Qurra's Theorem

The theorem of Thābit ibn Qurra is a method for discovering friendly numbers invented in the IX century by the Arab mathematician Thábit ibn Qurra.

State yes

p = 3\times2 n - 1 - 1

q = 3\times2 n - 1

r = 9\times2 2 n - 1 - 1

where $n > 1$ is an integer and $p$ , $q$ and $r$ are prime numbers, so $2 n \times p \times q$ and $2 n \times r$ are a pair of friendly numbers. This formula gives the pairs $(220, 284)$ for $n = 2$ , $(17296, 18416)$ for $n = 4$ and $(9363584, 9437056)$ for $n = 7$ , but no other pairs are known. Numbers of the form $3\times2 n - 1$ are known as Thabit numbers. For Ibn Qurra's formula to produce a friendly pair, two consecutive Thabit numbers must be prime; this severely restricts the possible values of $n$ .

To establish the theorem, Thâbit ibn Qurra proved nine lemmas divided into two groups. The first three lemmas deal with the determination of the aliquot parts of a natural number. The second group of lemmas deals more specifically with the formation of perfect, abundant, and deficient numbers.

Euler's Rule

Euler's rule is a generalization of Thâbit ibn Qurra's theorem. He affirms that yes

p = n - m + 1)\times2 m - 1

q = n - m + 1)\times2 n - 1

r = n - m + 1) 2 \times2 m + n - 1

where $n > m > 0$ are integers and $p$ , $q$ and $r$ are prime numbers, so $2 n \times p \times q$ and $2 n \times r$ are a pair of friendly numbers. Thābit ibn Qurra's theorem corresponds to the case $m = n - 1$ . Euler's rule creates additional friendly pairs for $(m, n) = (1,8), (29,40)$ with no others known. Euler (1747 and 1750) overall found 58 new pairs, bringing the number of known pairs to 61.

Regular Pairs

Let ( $m$ , $n$ ) a friendly number pair with $m < n$ . Now denote $m = gM$ and $n = gN$ where $g$ is the greatest common divisor of $m$ and $n$ . If $M$ and $N$ are both numbers coprime to $g$ and free of squares then the pair ( $m$ , $n$ ) is regular (sequence A215491 in OEIS); otherwise, it is called irregular or exotic. if ( $m$ , $n$ ) is regular and $M$ and $N$ have $i$ and $j$ prime factors respectively, then $(m, n)$ is said to be of type $(i, j)$ .

For example, with $(m, n) = (220, 284)$ , the greatest common factor is $4$ and therefore $M = 55$ and $N = 71$ . Therefore, $(220, 284)$ is a regular of type $(2, 1)$ .

Couples of twin friends

A pair of friends $(m, n)$ is the twin of another if there are no integers between $m$ and $n$ belonging to another friendly couple (sequence A273259 in OEIS).

Other results

In all known cases, the numbers in a pair are either both even or both odd. It is not known if there are pairs of friendly numbers made up of an even and an odd number, but if there is, the even number must be a square number or twice one, and the odd number must be a square number. However, friendly numbers exist in which the two members have different smaller prime factors: seven such pairs are known. Furthermore, every known pair shares at least one common prime factor. It is not known if there is a pair of friendly numbers that are coprime numbers, although if there are, the product of the two must be greater than 10⁶⁷. Furthermore, a pair of coprime friendly numbers cannot be generated by Thabit's formula (above), or by any similar formula.

In 1955, Paul Erdős proved that the density of friendly numbers, relative to positive integers, was 0.

In 1968, Martin Gardner observed that most pairs of friends known in his time have sums divisible by 9, and a rule was derived to characterize the exceptions (sequence A291550 in OEIS).

According to the Friendly Pairs Sum Conjecture, as the number of friendly numbers approaches infinity, the percentage of the sums of friendly pairs divisible by ten approaches 100% (sequence A291422 in OEIS).

There are pairs of Gaussian friends.

References in popular culture

Friendly numbers appear in the novel The Housekeeper and the Professor Yōko Ogawa and the Japanese film based on her.
The collection of short stories by Paul Auster entitled True Tales of American Life contains a story ('Afrodisiac mathematician' by Alex Galt) in which friends numbers play an important role.
Friendly numbers appear briefly in the novel The Stranger House Reginald Hill.
Friendly numbers are mentioned in the French novel The Loro Theorem Denis Guedj.
Friendly numbers are mentioned in the JRPG Shin Megami Tensei: Person 4.
Friendly numbers appear in the visual novel Rewrite.
Friendly numbers (220, 284) are mentioned in episode 13 of Korean drama And of 2017.
Friendly numbers appear in the Greek film The Other Me.
Friendly numbers are analyzed in Brian Clegg's book Are the numbers real?
Friendly numbers are mentioned in the 2020 novel Apeirogon Colum McCann.

Generalizations

Friend tuples

Friends numbers ${displaystyle (m,n)}$ satisfying that ${displaystyle sigma (m)-m=n}$ and ${displaystyle sigma (n)-n=m}$ that can be written together ${displaystyle sigma (m)=sigma (n)=m+n}$ . This can be generalized to larger tuples, such as ${displaystyle (n_{1},n_{2},ldotsn_{k})}$ where it is required

{displaystyle sigma (n_{1})=sigma (n_{2})=dots =sigma (n_{k})=n_{1}+n_{2}+dots +n_{k}}

For example, (1980, 2016, 2556) is a triplet of friendly numbers (sequence A125490 in OEIS) and (3270960, 3361680, 3461040, 3834000) is a (sequence A036471 in OEIS) quadruplet of friendly numbers.

Multisets of friends are defined analogously and generalize this concept a bit more (sequence A259307 in OEIS).

Sociable Numbers

Main article: Sociable numbers

The sociable numbers are the numbers in cyclical lists of numbers (with a length greater than 2) where each number is the sum of the dividers of the previous number. For example, ${displaystyle 1264460mapsto 1547860mapsto 1727636mapsto 1305184mapsto 1264460mapsto dots }$ are sociable numbers of order 4.

Search for sociable numbers

An liquid succession can be represented as a directed graph, ${displaystyle G_{n,s}}$ for an integer $n$ Where ${displaystyle s(k)}$ denotes the sum of the dividers own $k$ . Cycles in ${displaystyle G_{n,s}}$ represent the sociable numbers within the interval ${displaystyle [1,n]}$ . Two special cases are the loops that represent the perfect numbers and cycles of length two that represent friends numbers.

Contenido relacionado

Más resultados...