Four color theorem
In graph theory, the four color theorem (or chromatic minimality theorem) is a theorem about graph coloring that states the following:
|
Assuming that adjacent regions share not just one point, but an entire edge segment (border) in common.
Three colors are sufficient for simple maps, but in some cases an additional fourth color is necessary, that is, when a region to be colored is enclosed by an odd number of regions touching in a cycle. The five color theorem, whose proof is short and elementary, states that five colors are enough to color a map and was proven in the century. XIX by Heawood. A number of false proofs and false counterexamples have appeared since the first statement of the four-color theorem in 1852.
The four-color map problem was first posed by the student Francis Guthrie in 1852, which was communicated to Augustus de Morgan. The conjecture became famous with the statement of Arthur Cayley, in 1878, in the sense that he had approached it. It was solved, in the mid-1970s, by Kenneth Appel and Wolfgang Haken.
Precise formulation of the theorem
First of all, all corners and commonalities that belong to three or more countries should be ignored. Without this restriction, strange maps (using regions of finite area but infinite perimeter) may require more than four colors.
Second, for the purpose of the theorem each "country" it has to be a simply connected or continuous region. In the real world, this is not true (for example, Alaska as part of the United States, Nakhchivan as part of Azerbaijan, Kaliningrad as part of Russia, or Bolivia as part of Spain are not continuous regions). Because the territory of a particular country must be the same color, if "countries" non-continuous, four colors might not be enough. For example, consider a simplified map:
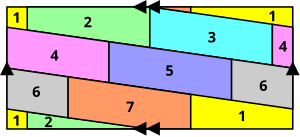
In this map, the two A regions belong to the same country, and therefore must be the same color. Consequently, this map requires five colors, since the two A regions are contiguous with the other four regions, and each of these regions are contiguous with each other. If there are three A regions, then six or more colors are needed; you can build maps that require an arbitrarily large number of colors. A similar scenario can also occur if the color blue is reserved for water.
A simpler version of the theorem uses graph theory. The set of regions of a map can be represented more abstractly as a simple undirected graph by associating a vertex for each region and an edge for each pair of regions that share an edge segment. This representation of the map with vertices and edges is a dual graph and the problem of coloring countries is changed by the coloring of the graph. This graph is flat, that is, it can be drawn in the plane without crossing edges by placing each vertex in an arbitrarily chosen place within the region to which it corresponds. Using the terminology of graph theory, the four-color theorem states that:
|
That is, the vertices of each planar graph can be colored with a maximum of four colors so that no two adjacent vertices have the same color. χ(G) corresponds to the chromatic number.
History
The four-color theorem arose as a conjecture. In 1852 Francis Guthrie was a student of Augustus De Morgan and made this conjecture, which could not be proven by Guthrie, nor by his brother Frederick, who had also been a student of De Morgan's, nor by Sir William Rowan Hamilton, whom De Morgan wrote to him formulating the conjecture.
In 1879 Alfred Bray Kempe announced in the journal Nature that he had a proof for the conjecture. In 1890, Percy John Heawood found an error in Kempe's proof. Heawood could not prove that the conjecture was invalid, but he continued to work on map coloring, being able to prove that any map could be colored with five colors.
In 1976 the conjecture had a proof, thanks to Kenneth Appel and Wolfgang Haken, who used a computer for the proof, which generated multiple controversies in the mathematical environment.
The controversial demo
The four-color theorem was proved with the help of a computer. However, the proof is not accepted by all mathematicians since it would be impracticable due to its great amount of detail, so that a person would be unable to verify it manually. It only remains to accept the accuracy of the program, the compiler and the computer on which the test was executed.
Another aspect of the demo, which can be considered a negative, is its lack of elegance. A review that talks about the elegance of it, commented at the time of its publication, says:
“A good mathematical test is similar to a poem—but this is a phone book!”.
Currently, another demonstration was made, also using computer calculations, which verifies the original proof; but there is still no demo that does not make use of these methods.
Summary of demo ideas
The following summary is based on the book Every Planar Map is Four Colorable by Appel and Haken published in 1989. Although Kempe's proof of the four color theorem contained a flaw, it provided some of the basic tools used later to demonstrate it. The explanation given here has been restated using modern graph-theoretic terms.
Kempe's argument is as follows. First, if the graph has non-triangular planar regions or faces, that is, they do not have three edges as boundaries, edges can be added to the graph (without introducing new vertices) such that each region of the graph is triangular, including the region abroad. If this original triangular graph supports a coloring with four colors or less, then the initial graph also supports the same coloring (or a coloring with fewer colors), since the coloring is still valid if the introduced edges are removed. So it is enough to prove the theorem of the four colors for the particular case of triangular graphs to prove it to all planar graphs, and without loss of generality, we assume that the graph is triangular.
Suppose v, a, and c are the number of vertices, edges, and regions. Since each region is triangular and each edge is shared by two regions, we have that 2a = 3c. This, together with Euler's theorem formula for polyhedra (v - a + c = 2) can be used to show that 6v - 2a = 12. Now, the degree of a vertex is the number of incident edges. If vn is the number of vertices of degree n, and D is the maximum degree of a vertex, you have:
- 6v− − 2a=6␡ ␡ i=1Dvi− − ␡ ␡ i=1Divi=␡ ␡ i=1D(6− − i)vi=12.{displaystyle 6v-2a=6sum _{i=1}^{d}v_{i-sum _{i=1}^{d}iv_{i}=sum _{i=1}{d}{d}(6-i)v_{i}=12. !
But 12 > 0, is a positive number and "6 - i ≤ 0" for all "i ≥ 6", this shows that there is at least one vertex of degree 5 or less.
If there exists a graph that requires 5 colors, then there exists a minimal graph, where the removal of any vertex makes it four colorable. Let's call this graph G. The graph G cannot have a vertex of degree 3 or less, because if g(v) ≤ 3, we can eliminate v from G, and color the smallest modified graph with four colors, and then add back the vertex v and color it with a different color from its neighbors.
Kempe also proved that G cannot have any vertex of degree 4. As before, the vertex v is removed, and four colors of the remaining vertices. If the four neighbors of v are of different colors, say red, green, blue, and yellow clockwise, we look for an alternate path of red and blue vertices joining the red and blue neighbors. Such a path is called a Kempe chain. There may be a Kempe chain joining the red and blue neighbors, and there may be a Kempe chain joining the green and yellow neighbors, but not both, since these two paths necessarily intersect, and the vertex where they intersect cannot be colored. Suppose that red and blue neighbors are treated that are not chained to each other. Explore all the vertices connected to the red neighbor by the red-blue alternate paths, and then invert the red and blue colors at all these vertices. The result is still a valid four-color, and now v can be added again and colored red.
This leaves only the case where G has a vertex of degree 5; but Kempe's argument was flawed in this particular case. Heawood noted Kempe's error and also noted that if you were satisfied with proving that only five colors are necessary, you could use the above argument (changing the counterexample to one that requires 6 colors) and use the Kempe chains at the vertex of grade 5 to prove the five color theorem:
|
Generalizations
The problem of coloring other surfaces that are not equivalent to a plane has also been studied. For closed surfaces (orientable or non-orientable) with positive gender, the maximum number of p colors needed depends on the Euler characteristic χ, given by the following formula:
- p= 7+49− − 24χ χ 2 ,{displaystyle p=leftlfloor {frac {7+{sqrt {49-24chi }}}}{2}}rightrfloor}
where the outer parentheses determine the function integer part.
Alternatively, for an orientable surface, the formula can be given in terms of the sort of the surface, g:
- p= 7+1+48g2 {displaystyle p=leftlfloor {frac {7+{sqrt {1+48g}}}}{2}rightrfloor } (Weisstein).
This formula, known as Heawood's conjecture, was conjectured by P. J. Heawood in 1890 and proved for cases of unbounded orientable (and nonorientable) surfaces by Gerhard Ringel and J. T. W. Youngs in 1968. The only exception to the formula is the Klein Bottle, which has Euler characteristic 0 (hence the formula gives p=7) and requires 6 colors, as P. Franklin demonstrated in 1934 (Weisstein). (A Möbius Band, whose Euler characteristic χ = 0, also requires 6 colors, but in this case the formula is not applicable, since it is a bounded surface. (Weisstein))
The torus has an Euler characteristic χ = 0 (and genus g = 1) and therefore p = 7, so no more than 7 colors they are required to color any map about a bull. The Szilassi Polyhedron is another example that requires 7 colors.
There is no obvious extension of the problem of coloring regions of three-dimensional solids. Using a set of n flexible rods, one can make each rod touch each of the others. The set will then require n colors, or n+1 if empty space is considered to also touch each rod. For the number n you can take as large an integer as you like. such examples were proposed by Fredrick Gurthrie in 1880. (Wilson, 2002)
Contenido relacionado
International System Prefixes
MathML
Stochastic