Formal grammar

This image shows the relationship between character strings, well-formed formulas and theorems. In some formal systems, however, the set of the theorems coincides with that of well-formed formulas.

A formal grammar is a logical-mathematical structure with a set of formation rules that define the admissible character strings in a given formal language or natural language. Formal grammars appear in several different contexts: mathematical logic, computer science, and theoretical linguistics, often with divergent methods and interests.

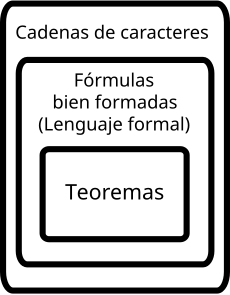
In a formal language, strings formed according to the rules of formal grammar are called well-formed formulas, and the set of all well-formed formulas constitutes a formal language. A formal grammar does not describe the meaning of well-formed formulas, only their form. The theory of formal languages studies formal grammars and formal languages, and is a branch of applied mathematics. Its applications are found in theoretical computational science, linguistics, formal semantics, mathematical logic, and other areas.

Introduction

A formal grammar is a set of rules for rewriting strings, together with a starting symbol from which the rewriting should begin. Therefore, a formal grammar is generally thought of as a generator of languages. However, it can also sometimes be used as the basis for a "matcher": a function that determines whether any given string belongs to a language or is grammatically incorrect.

There are different types of formal grammars that generate formal languages (see Chomsky's hierarchy). Imagine a grammar with these two rules:

1. A → bA
2. A → c

The uppercase element is the initial symbol. Elements in lowercase are the terminal symbols. To generate character strings, the idea is to replace the leading symbol on the left with the symbols on the right, and then repeat the process until there are only terminal symbols. For example:

A → bA → bbA → bbbA → bbbc

This grammar gives rise to a formal language that consists of the set of all character strings that can be generated by means of them. For example: bbbc, bbbbbbbbc, c, bc, etc.

To better understand the idea, we can consider a rewrite model for Spanish:

1. O → SUJ PRED (Order → Subject Preached)
2. SUJ → Det N (Subject → Determinant Name)
3. PRED → V COMP (Preached → Add-on Word)
4. DET →
5. N → child, (man, old)
6. V → sleep, (rie, eat)
7. COMP → quietly, (internalranquile)

These rules can be used to generate the phrase "the child sleeps peacefully", like so:

1. O(RATION) (initial symbol)
2. PRED (ICADO) (by rule 1)
3. DET(ERMINANT) N(OMBRE) PRED(ICADO) (by rule 2)
4. DET(ERMINANT) N(OMBRE) V(ERBO) COMP(LEMENT) (by rule 3)
5. the N(OMBRE) V(ERBO) COMP(LEMENT) (by rule 4)
6. the child V(ERBO) COMP(LEMENT) (by rule 5)
7. The child sleeps COMP(LEMENT) (by rule 6)
8. the child sleeps quietly (by rule 7)

We see that there are some special definitions such as SENTENCE, SUBJECT, etc. that do not appear in the final sentence formed. They are abstract entities called "syntactic categories" which are not usable in a sentence (they have a role similar to that of parts of speech in natural languages). And likewise the same system allows deriving other similar sentences using the lexical forms between parentheses:

Det	N	V	COMP
The	child man Old	Sleep. laugh. Eat.	plácida Inquire

Syntactic categories define the structure of the language representing more or less large portions of the sentences. There is an internal hierarchy between the syntactic categories.

The top category would be the SENTENCE that represents a valid sentence in Spanish.

Below it are its components. None of these categories give rise to valid phrases only the top category.

At the end of the entire hierarchy we arrive at the words that are the minimum units with meaning that a sentence can adopt.

By applying the hierarchies and substituting elements, we reach the point where all the syntactic categories have been converted into words, thus obtaining a valid sentence; such as: The boy is running. This process is called production or generation.

Formal grammars in theoretical linguistics

A formal grammar is a mathematical model (more exactly an algebraic structure) composed of a series of syntactic categories that are combined with each other by means of syntactic rules that define how a syntactic category is created by means of others or symbols of the grammar. There are several types of historically important formal grammars:

• The categorial formal grammar (C-grams) that use an analysis below and require the use of category labels for each sequence formed or constituting syntactic properly said. There is a single higher category that denotes complete and valid chains.
• The syntagmatic structure grammar (ES-gramsin English PS-grammars) based on rewriting rules and with a top-down analysis. Like the C-grams are based on the notion of syntactic constituents.
• The associative grammar (on the left) (A-gramsin English LA-grammars), which uses an analysis from the bottom up, which allows an analysis of linear complexity, although they ignore the concept of syntactic constituent.

The first two types have obvious points of connection with the notion of syntactic constitution and parsing by syntactic trees. However, parsers for sentences formed according to them cannot rely on generation rules (speaker-listener asymmetry), which suggests that they cannot be good models of speaker intuition. In addition, the natural language models based on them seem to have a polynomial or exponential complexity, which does not seem to agree with the speed with which speakers process natural languages. On the other hand, A-grammars in general have linear complexity, symmetry between speakers and listeners, however, they ignore the classical constituents of syntactic analysis. However, they are still used for parsers used in computing.

By means of these constituent elements, a specification mechanism is defined consisting of repeating the mechanism of substitution of a category by its constituents according to the rules starting with the superior category and ending when the sentence no longer contains any category. In this way, the grammar can generate or produce each of the strings of the corresponding language and only these strings.

Definition of a C-grammar

A categorical grammar or C-grammar is one based on grammatical categories. The lexical forms and sequences formed from them are labeled with categories that indicate the type of entity formed and their combinatory possibilities (for example, in a noun language a sequence of words can constitute a noun phrase which specifies with what other types of categories This phrase can be combined to form another major phrase).

categorial grammars can be defined as an algebraic formal structure. A grammar is a cyntuplate ${displaystyle scriptstyle (W,C,LX,R,CE)}$ with the following properties:

1. ${displaystyle scriptstyle W}$ (words) is the non-empty set of well formed forms of the tongue (in a natural language W could be interpreted as sequences of seals that form expressions, irrespectively of their grammatical category).
2. ${displaystyle scriptstyle C}$ (categories) is the non-empty set of possible categories. For this set to be an acceptable set of categories, it is required if ${displaystyle scriptstyle X,Yin C}$ then there are also categories ${displaystyle scriptstyle X{bar {Y}in C}$ (frequently denoted as well as And/X) and ${displaystyle scriptstyle {bar {Y}Xin C}$ (frequently denoted as well as AndX). Note that the above results from the existence of the categories ${displaystyle scriptstyle X{bar {Y}in C}$ and ${displaystyle scriptstyle {bar {Y}Xin C}$ (without sharing the role of X e And).
3. The whole ${displaystyle scriptstyle LX}$ (lexicon) is a set ${displaystyle scriptstyle LXsubset Wtimes C}$, this set is somewhat different from the conventional lexicon as it includes both inanalyzable atomic words and expressions formed from them.
4. The whole ${displaystyle scriptstyle R}$ (rules) is a set of rules, usually formed by the following two rules:
   1. ${displaystyle alpha _{X{bar {Y}}}circ beta _{Y}rightarrow alpha beta _{X}}}$
   2. ${displaystyle beta _{Y}circ alpha _{{bar {Y}X}rightarrow alpha beta _{X}}}}$

   The above apply to any categories and are thus interpreted: if in a formal language the elements on the left of the rule belong to the lexicon ${displaystyle scriptstyle LX}$, then the expression on the right of the rule is also part of the lexicon (i.e. of the set of possible expressions in that language). It is understood that since the composition may be on the left (rule 1) or on the right (rule 2) it has been required that the whole ${displaystyle scriptstyle C}$ in addition to categories ${displaystyle scriptstyle X}$ e ${displaystyle scriptstyle Y}$ categories ${displaystyle scriptstyle X{bar {Y}}}$ and ${displaystyle scriptstyle {bar {Y}X}$.

5. The whole ${displaystyle scriptstyle CE}$ (complete expressions)

Definition of an ES-grammar

In the classic definition given by Noam Chomsky in the 1950s, a formal phrase-structure grammar (ES-grammar) is a quadruple G = (N,T,S,P) where:

• N is a finite set of non-stop symbols (variable).
• T is a finite set of terminal symbols (counters), disjoined with N.
• S is a distinguished symbol of N, the initial symbol.
• P is a finite set of production rules, each shape:

${displaystyle (Ncup T)^{*}N(Ncup T)^{*}$

where * is the closing of Kleene. This is, each production rule maps from one chain of symbols to another, where the first string contains at least one non-stop symbol. In the event that the second chain is the empty chain, to avoid confusion it is denoted with a special notation (usually ${displaystyle epsilon ,}$, ${displaystyle e,}$ or ${displaystyle lambda ,}$).

The alphabet of grammar is then the whole ${displaystyle sigma =Ncup T}$

Derivations

Sea ${displaystyle G=(N,T,P,S)}$ a grammar, and be α, β, δ, φ, ρ,... words of ${displaystyle sigma ^{}}$. Then:

• β derived of α in a step of derivation, and we denote it with α ${displaystyle Rightarrow }$ β if there are two strings ${displaystyle phi _{1},phi _{2}in sigma ^{*}}$, and a production δ → ρ such that α = ${displaystyle phi _{1}}$ δ ${displaystyle phi _{2}}$, and β = ${displaystyle phi _{1}}$ ρ ${displaystyle phi _{2}}$
• We note with ${displaystyle Rightarrow ^{{}}$ to reflective and transitive closure ${displaystyle Rightarrow }$. I mean α ${displaystyle Rightarrow ^{{}}$ β denotes a sequence of derivations in a finite number of steps from α to β.
• ${displaystyle xin sigma ^{*}$ It's a sentencing form of ${displaystyle G}$if the following sequence of derivations can be obtained ${displaystyle SRightarrow ^{*}x}$. In the particular case of ${displaystyle xin T^{}}$ it is said that x is a Judgement
• It is called formal language generated by G to the whole ${displaystyle L(G)={xin T^{*}{Rightarrow ^{*}x}}$

Chomsky's Hierarchy

When Noam Chomsky formalized the idea of generative grammars in 1956, he classified generative grammars into various types of increasing complexity that form the so-called Chomsky hierarchy. The difference between these types is that each one of them has more particular and restricted rules and therefore they generate less general formal languages. Two important types are context-free grammars (Type 2) and regular grammars (Type 3). The languages that can be described by these types of grammars are context-free languages and regular languages, respectively. These two types are much less general than Type 0 unrestricted grammars (ie they can be processed or recognized by Turing machines). These two types of grammars are used more frequently since parsers for these languages can be implemented efficiently. For example, all regular languages can be recognized by a finite automaton. For subsets of context-free grammars, there are algorithms for generating efficient LL parsers and LR parsers, which allow recognizing the corresponding languages generated by those grammars.

Limitation of formal grammars

ES-grammars like the one used in early generative grammar models require certain restrictions to be computationally tractable. To understand this restriction, the interaction between a speaker and a listener must be considered, the first generates a sentence or sequence according to the rules of grammar, the second to understand said sequence must analyze the sequence to understand it, finding the forming elements, interpreting them. and reconstructing the relationship between them (internal structure). For this second to be possible, it is required that the internal structure have a sufficiently simple structure to be able to parse the sequences with a low degree of ambiguity. Well, computationally it has been found that the complexity class against the inverse analysis of certain grammars is excessive. For ES-grammars based on rewriting rules we have:

Formal grammars in mathematics and logic

Within the formalist and axiomatic approach to mathematics, it was conceived that certain areas of mathematics could be conceived as a logical-deductive system of formulas subject to manipulation restrictions. The formal grammar of these systems would be the set of combinatorial rules according to certain deductive principles.

A formal language in logic or mathematics is a triplet ${displaystyle scriptstyle (A,R_{F},{mathcal {A}},{mathcal {D}}}}$ where ${displaystyle scriptstyle A}$ denotes the alphabet or set of used signs, the set of rules ${displaystyle scriptstyle R_{F}}$ explains what combinations of signs are well defined and allows to define what is a well-formed formula (in that sense ${displaystyle scriptstyle R_{F}}$ defines the morphology of the words of the formal language. The set of well-formed formulas constitute vocabulary or lexicon, while the pair ${displaystyle scriptstyle ({mathcal {A}},{mathcal {D}}}}}}$ describes the set of axioms and the set of valid deduction rules. The latter two allow to establish sequences of well-formed formulas (words of formal language) that constitute valid demonstrations within the formal system (they are somehow the equivalent of the syntax of the formal language).