Finite automaton

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

A finite automaton (AF) or finite state machine is a computational model that automatically performs computations on an input to produce an output.

This model is made up of an alphabet, a set of finite states, a transition function, an initial state, and a set of final states. Its operation is based on a transition function, which receives from an initial state a string of characters belonging to the alphabet (the input), and which reads said string as the automaton moves. from one state to another, to finally stop at a final state or acceptance state, which represents the exit.

The purpose of finite automata is to recognize regular languages, which correspond to the simplest formal languages according to Chomsky's Hierarchy.

History

McCulloch-Pitts' neuronal model also uses diagrams with states and transitions, as well as input and output concepts.

The origin of finite automata probably dates back to their implicit use in electromechanical machines, from the early 20th century. As early as 1907, the Russian mathematician Andrei Markov formalized a process called the Markov chain, where the occurrence of each event depends with a certain probability on the previous event. This ability to "remember" it is later used by finite automata, which have a similar primitive memory, in which the activation of a state also depends on the previous state, as well as the symbol or word present in the transition function.

Subsequently, in 1943, a first formal approximation of finite automata emerged with the McCulloch-Pitts neural model. During the 1950s their study proliferated, often being called sequence machines; many of their basic properties are established, including their interpretation as regular languages and their equivalence with regular expressions. At the end of this decade, in 1959, the concept of non-deterministic finite automata arose in the hands of computer theorists Michael O. Rabin and Dana Scott.

In the 1960s their connection to power series and overwriting systems was established. Finally, with the development of the Unix operating system in the 1970s, finite automata found their niche in the massive use of regular expressions for practical purposes, specifically in the design of lexical analyzers (lex command) and text search and replace (ed and grep commands). From that time, finite automata also began to be used in dynamical systems.

Formal definition

Formally, a finite automaton is a 5-tuple (Q, Σ, q₀, δ, F) where:

$Q,$ is a finite set of states;
$Sigma ,$ He is a finite alphabet;
$q_{0}in Q$ is the initial state;
$delta colon Qtimes Sigma to Q$ is a transitional function;
$Fsubseteq Q$ is a set of final or acceptance states.

Representation as state diagrams

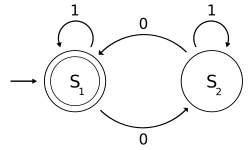
This finite automaton is defined on the alphabet σ={0,1}, has two states s₁ and s₂, and their transitions are δ(s₁,0)=s₂, δ(s₁,1)=s₁, δ(s₂,0)=s₁ and δ(s₂,1)=s₂. Your initial status is s₁which is also its only final state.

Finite automata can be represented by particular graphs, also called finite state diagrams, as follows:

The states Q are represented as vertices, labeled with their name on the inside.
A transition δ from one state to another, dependent on a symbol of the alphabet, is represented by a directed edge that binds these vertices, and is labeled with that symbol.
Initial status q₀ is characterized by having an arist that comes to it, coming from no other vertex.
The or the final states F they are represented by vertices that are locked in turn by another circumference.

Representation as transition table

Main article: State transition table

Another way to describe the operation of a finite automaton is by using transition tables or state matrices. Two possible tables for the example of the previous image could be the following:

Output q 한 Q	symbol σ ⋅	arrival δ(q,σ) 한 Q
s₁	0	s₂
s₁	1	s₁
s₂	0	s₁
s₂	1	s₂

	0	1
*→s₁**	s₂	s₁
s₂	s₁	s₂

The first one explicitly represents the parameters and the value that each occurrence of the transition function takes. The second one is more compact, and marks the initial state with an arrow, and the final states with an asterisk.

Operation

The general scheme is that of a reading tape that advances only forward and to a cell, according to the transitional function.

At the beginning of the process of recognizing an input string, the finite automaton is in the initial state and as it processes each symbol in the string it changes state according to what is determined by the transition function. When the last of the symbols in the input string has been processed, the automaton stops in the final state of the process. If the final state at which it stopped is an accepting state, then the string belongs to the language recognized by the automaton; otherwise, the string does not belong to that language.

Note that the initial state $q_{0}$ of a finite automaton is always unique, while the final states can be more than one, that is, the whole $F$ can contain more than one element. There can also be the case that a final state corresponds to the same initial state.

Generalization of the transition function

If Σ is an alphabet, then Σ* is denoted by the set of all strings of characters or words that can conform to that alphabet.

A δ transition function can be generalized to a δ* function, which operates on states and sequences of symbols, rather than individual symbols of the alphabet. Thus, this new transitional function is defined $delta ^{*}colon Qtimes Sigma ^{*}to Q$ , allowing to characterize automatons more abbreviated and without losing expressivity.

The function δ* can also be expressed recursively, defining for every string x ∈ Σ*, every symbol a ∈ Σ, and a state q ∈ Q:

$delta ^{*}(q,epsilon)=q,$ which is the inductive base, being ε the empty chain, and
$delta ^{*}(q,xa)=delta (delta ^{*}(q,x),a),$ which is the induction itself.

The configuration of a finite automaton at an "instant" in machine computing; that is, the current state of said computation, together with the word that has been processed up to that moment. Formally, it is defined as an ordered pair (q, x) ∈ Q × Σ*. In this way, the initial configuration of the automaton can also be defined, such as the pair (q₀,x), where x is the input; and the final configuration, as the pair (q,ε), with q ∈ F.

Thus, the regular language accepted by a finite automaton A can be denoted as L(A) = {w; δ^*(q₀,w)∈ F}, that is, as the set of all initial configurations that lead to final states.

Deterministic finite automaton

AFD that recognizes the regular language formed exclusively by strings with a pair of zeros and pairs of ones.

Main article: Determinist finite

A deterministic finite automaton (abbreviated AFD) is a finite automaton that is also a deterministic system; that is, for each state q ∈ Q in which the automaton is, and with any symbol a ∈ Σ of the read alphabet, there always exists at most one possible transition δ(q,a).

In an AFD neither of these two cases can occur:

That there are two transitions of the type δ(q,a♪q₁ and δ(q,a♪q₂, being q₁ I was. q₂;
That there are transitions of the type δ(q, ε), except q be a final state, without transitions to other states.

An interesting type of deterministic finite automata are called acyclics and an example of these are tries.

Nondeterministic finite automaton

AFND with δ(q₀,b♪q₀ and δ(q₀,b♪q₁which accepts the regular language on the alphabet {a,b} conformed by all the words that end in b; i.e. equivalent to regular expression (aUDIB)*b⁺.

AFND-ε to which state 2 can be accessed via state 3, without processing input symbols.

Main article: Automata finito no determinista

A nondeterministic finite automaton (abbreviated AFND) is one that, unlike deterministic finite automata, possesses at least one state q ∈ Q, such that for a symbol a ∈ Σ of the alphabet, there exists more than one transition δ(q,a) possible.

Making the analogy with AFDs, in an AFND either of these two cases can occur:

That there are transitions of the type δ(q,a♪q₁ and δ(q,a♪q₂, being q₁ I was. q₂;
That there are transitions of the type δ(q, ε), being q a non-final state, or a final state, but with transitions to other states.

When the second case holds, the automaton is said to be a nondeterministic finite automaton with empty transitions or ε-transitions (abbreviated AFND-ε). These transitions allow the automaton to change state without processing any input symbols.

Formally, it is distinguished from the 5-tuple that defines a deterministic finite automaton in its transition function. While in an AFD this function is defined as follows:

delta:Qtimes Sigma to Q

in an AFND is defined as:

delta:Qtimes Sigma to {mathcal {P}}(Q)

In the case of AFND-ε, the transition function is usually expressed in the form:

delta:Qtimes {Sigma cup epsilon }to {mathcal {P}}(Q)

where P(Q) is the power set of Q.

This means that deterministic finite automata are a particular case of non-deterministic automata, since Q belongs to the set P(Q).

The interpretation that is usually made in the computation of an AFND is that the automaton can be in several states at the same time, generating a branch of the configurations existing at a given moment. Another interpretation can be to imagine that the machine "guess" to which state it should go, choosing a transition among several possible ones.

Note finally that in a non-deterministic finite automaton we can accept the existence of more than one initial node, further relaxing the original definition.

Equivalences between finite automata

Two finite automata are said to be equivalent, if they both recognize the same regular language.

Any regular expression (which in turn defines a regular language) can be expressed as a deterministic finite automaton, and vice versa. Given a regular expression, it is possible to construct an AFND-ε that recognizes that language, for example by Thompson's algorithm. Then, every AFND-ε can be transformed into an equivalent AFND, just as every AFND can be transformed into an equivalent AFD, through the method called power set construction. Thus, by transitivity, for any nondeterministic finite automaton there always exists an equivalent deterministic finite automaton, and vice versa.

Normally in the design of finite automata, the first thing to do is build an AFND-ε, which is the easiest to build, as it has fewer restrictions on its transition function. Then said automaton is reduced to an AFND, and finally to an AFD, which due to its deterministic characteristics can already be implemented without problems using a programming language.

Conversion of an AFND-ε to an AFND

The conversion of an AFND-ε into an AFND is based on the concept of closure-ε, which corresponds to a transitive closure contextualized in automata theory.

Given a state q, the set of all states that can be accessed is closure-ε(q). starting from q, processing at most a single symbol from the input. It can be defined recursively as follows:

(Inductive base) For everything q, q certified closed-ε(q).
(Induction) Given two states p and rYeah. p certified closed-ε(q) and r certified δ(p,ε), then r certified closed-ε(q).

The algorithm to remove empty transitions is as follows:

The closing-ε of the initial state is calculated, forming a set A which will correspond to the initial state of the new automaton.
For each alphabet symbol, the achievable states are verified from a state contained in Aand the closing-ε of such achievable states is calculated. If such closures produce new sets other than A, these will be new states that will be accessed from A and the corresponding symbol.
The above is repeated for each new set, until there are no possible transitions for any alphabet symbol.

Example

Elimination of empty transitions from an AFND-ε.

AFND-ε initial.

In this case you get an AFD, which is a particular case of AFND.

In the example of the figure, we will initially have:

Closure-ε(1= {1,2,3,4,6} = A

Stop. A:

For the symbol a: 4 goes to 5, and closing-ε(5= {5.7} = B.

For the symbol b: there are no possible transitions.

Stop. B:

For the symbol a: there are no possible transitions.

For the symbol b: 5 going to 6, and closing-ε(6- = {6} = C.

Stop. C:

For the symbol a: there are no possible transitions.

For the symbol b: there are no possible transitions.

This concludes the algorithm and the automaton of the figure is obtained.

In some cases it may happen that by removing the epsilon transitions we directly obtain an AFD, since the only reason for non-determinism was precisely the presence of said transitions.

Conversion from an AFND to an AFD

Main article: Construction of subsets

Conversion of an AFND to an AFD.

Initial AFND.

Conversion process.

Final AFD.

All AFND (Q_N, Σ, q₀, δ_N, F_N) can become an AFD (Q_D, Σ, q₀, δ_D, F_D) equivalent, keeping the alphabet Σ and the initial state q₀ originals. The conversion involves going through an intermediate AFD with redundant states and transitions, which, since they are not accessible from the initial state, are eliminated to obtain the final AFD.

To define the intermediate AFD, the following steps must be followed:

First the set of states is redefined Q_N =q₀, q₁,... q_mOriginal, as one made up of all subsets Q_N. The new final states will be all those states that contain any of the original final states.
Subsequently, the set of original transitions is redefined, by transitions of the type δ_D(S,aWhere a한, and S is the union of all states q of Q_N for which there was the transition δ_N(q,a).
Finally, the inaccessible states or inalcanzables (together with their departure transitions), that is, those to which you cannot access from the initial state. After this cleansing, you get the final AFD.

Example

In the example figures, as the initial AFND has three states (q₀, q₁, q₂), then the intermediate DFA will have seven ({q₀}, {q ₁}, {q₂}, {q₀, q₁}, {q₀, q₂}, {q₁, q₂}, {q ₀, q₁, q₂}), and as the final state original was q₂, then the final states of the intermediate DFA are {q₂}, { q₀, q₂}, {q₁, q₂} and {q₀, q₁, q₂}. Regarding the new transitions, note for example that the transition δ_N(q₀,1) was kept)=q₀, now called δ_D({q₀},1)={q₀}; however, since it was originally given that δ_N(q₀,0)=q ₀ and δ_N(q₀,0)= q₁, now these two transitions were replaced by δ_D({q₀},0)={q₀, q₁}. Finally, note that the states {q₁}, {q₂}, and {q ₁, q₂} are not connected to the rest of the automaton that has the initial state; therefore, they are eliminated. Also {q₀, q₁, q_{is also removed 2}}, because despite being connected to the rest of the automaton, it is not accessible from {q₀}. Thus, finally, eliminating these four states, as well as their respective transitions, the AFD sought is obtained.

Minimization of an AFD

Two states of a deterministic finite automaton are equivalent states if, when united into a single state, they can recognize the same regular language as if they were separated. This union of states implies the union of both its input and output transitions. If two states are not equivalent, they are said to be distinguishable states. A final state with a non-final state will never be equivalent.

An AFD is minimized, if all its states are distinguishable and reachable. An AFD minimization algorithm is as follows:

Eliminate the inaccessible states of automaton.
Build a board with all pairs (p, q) of remaining states.
Mark in the table those entries where one state is final and the other is non-final, that is, those pairs of states that are clearly distinguishable.
For each pair (p, q) and each symbol a of the alphabet, r = δ(p,a) and s = δ(q,a(c):
1. Yeah.r, s) has already been marked, then p and q are also distinguishable, therefore mark the entrance (p, q).
2. Otherwise, place (p, q) in a list associated with the entry (r, s).
Group the pairs of unmarked states.

After the third step, if the created table is completely marked, then the initial AFD was already minimal.

The computational complexity of the problem of minimizing an AFD is polynomial. In fact, there are even more efficient algorithms than the one shown in this article (although less intuitive). However, the problem of minimizing a non-deterministic finite automaton is NP-complete and PSPACE-complete.

Example

Minimization of an AFD.

AFD with redundant states.

AFD minimized.

The first figure in the example shows an automaton with the inaccessible state d, which can be removed immediately. Then the table of state pairs is built, and then, according to the third line of the algorithm, the rows and columns corresponding to the final states c and g are marked., except for the cell that represents the pair (c,g), since since both are final states, they can be equivalent states. Subsequently, the remaining cells are marked according to the fourth line of the algorithm, noting that the pair (b, f) is associated with the pair (c, g), and thus finally the final automaton is obtained, grouping the states b and f, as well as c and g, as shown in the second figure of the example.

Tables for the search for equivalent states

b
c
e
f
g
	a	b	c	e	f

b
c
e
f
g
	a	b	c	e	f

b
c
e
f
g
	a	b	c	e	f

Generalizations of finite automata

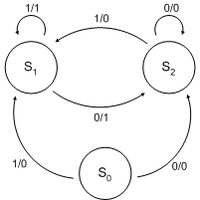
Example of Mealy Machine, a type of finite state transducer, which generalizes finite automatons.

There are several possible generalizations to make about finite automata, to increase their usability and expressiveness. Thus, for example, finite state transducers are defined as finite automata that are also endowed with an output alphabet, different from the input one, and that can have more than one initial state. Moore machines and Mealy machines are Well-known examples of transducers, which are mainly used to model sequential systems.

It is even possible to increase the computational power of a finite automaton, allowing an additional alphabet on it, acting on a stack type memory to be considered in each transition. This is the idea used by so-called stack automata, which are capable of recognizing context-free languages, which are one level above regular languages in Chomsky's Hierarchy.

Contenido relacionado

Más resultados...