Fibonacci sequence
In mathematics, the Fibonacci sequence is the following infinite sequence of natural numbers:
610, 987, 1597ldots ,</math>.
The sequence begins with the numbers 0 and 1; from these, "each term is the sum of the two previous ones", is the recurrence relation that defines it.
The elements of this sequence are called Fibonacci children. This sequence was described in Europe by Leonardo of Pisa, an Italian mathematician of the 13th century also known as Fibonacci >. It has numerous applications in computer science, mathematics, and game theory. It also appears in biological configurations, such as in the branches of trees, in the arrangement of the leaves on the stem, in the flowers of artichokes and sunflowers, in the inflorescences of Romanesque broccoli, in the configuration of the cones of conifers., in rabbit reproduction, and in how DNA codes for the growth of complex organic forms. Similarly, it is found in the spiral structure of the shell of some mollusks, such as the nautilus.
History
Leonardo Pisano, Leonardo of Pisa, or Leonardo Bigollo, also known as Fibonacci, was born in 1170 and died in 1240. Long before it was known in the West, the Fibonacci sequence was already described in mathematics in India, in connection with Sanskrit prosody.
Susantha Goonatilake notes that the development of the Fibonacci sequence "is partly attributed to Pingala (c. 200), later associated with Virahanka (c. 700), Gopāla (c. 1135) and Hemachandra (c. 1150)". Parmanand Singh cites Pingala (c. 450) as a forerunner in the discovery of the sequence.
The sequence was described and made known in the West by Fibonacci as the solution to a rabbit breeding problem:
| Number of month | Explanation of genealogy | Couples of rabbits |
|---|---|---|
| Beginning of the month 1 | A couple of rabbits are born (part A). | 1 couple in total. |
| End of the month 1 | Couple A is one month old. You cross the A pair. | 1+0=1 couple in total. |
| End of the month 2 | Couple A gives birth to couple B. It crosses the A pair again. | 1+1=2 pairs in total. |
| End of the month 3 | Couple A gives birth to couple C. Couple B turns 1 month. Couples A and B cross. | 2+1=3 pairs in total. |
| End of the month 4 | Couples A and B give birth to D and E. Couple C turns 1 month. Couples cross A, B and C. | 3+2=5 pairs in total. |
| End of the month 5 | A, B and C give birth to F, G and H. D and E serve a month. They cross A, B, C, D and E. | 5+3=8 pairs in total. |
| End of the month 6 | A, B, C, D and E give birth to I, J, K, L and M. F, G and H each month. They cross A, B, C, D, E, F, G and H. | 8+5=13 couples in total. |
| ... | ... | ... |
| ... | ... | ... |
Note: by counting the number of different letters in each month, you can find out the total number of pairs up to that month.
This is how Fibonacci presented the sequence in his book Liber Abaci, published in 1202. Many properties of the Fibonacci sequence were discovered by Édouard Lucas, responsible for having named it as it is known in the present.
Also Kepler described Fibonacci numbers, and Scottish mathematician Robert Simson discovered in 1753 that the relationship between two successive Fibonacci numbers fn+1/fn{displaystyle f_{n+1}/f_{n}} approaching the golden relationship fi (φ φ {displaystyle phi }) when n{displaystyle n} tends to infinity; it is more: the quotient of two successive terms of any recurring succession of order two tends to the same limit. This succession had popularity in the centuryXX. especially in the musical sphere, in which composers with both renowned and Béla Bartók, Olivier Messiaen, the band Tool and Delia Derbyshire used it for the creation of chords and new structures of musical phrases.
Recurring definition
Fibonacci numbers are defined by the equations
(1)f0=0{displaystyle f_{0}=0,}
(2)f1=1{displaystyle f_{1}=1,}
(3)fn=fn− − 1+fn− − 2{displaystyle f_{n}=f_{n-1}+f_{n-2},}
This produces the following numbers:
- f2=1{displaystyle f_{2}=1,}
- f3=2{displaystyle f_{3}=2,}
- f4=3{displaystyle f_{4}=3,}
- f5=5{displaystyle f_{5}=5,}
- f6=8{displaystyle f_{6}=8,}
- f7=13{displaystyle f_{7}=13,}
- f8=21{displaystyle f_{8}=21,}
and so on.
This way of defining, in fact considered algorithmic, is usual in discrete mathematics.
It is important to define f0=0{displaystyle f_{0}=0,} so that the important property can be complied with:
fn{displaystyle f_{n}} divide a fm↓ ↓ n{displaystyle f_{m*n}For any =1}" xmlns="http://www.w3.org/1998/Math/MathML">m,n▪1{displaystyle m,n rigid=1}=1" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/41f03ee0b1d3f950472801ae5ae59353161d1e25" style="vertical-align: -0.671ex; width:10.538ex; height:2.509ex;"/>.
Alternative representations
To analyze the Fibonacci sequence (and, in general, any sequence) it is convenient to obtain other ways of representing it mathematically.
1± ± 52=ba=cb{displaystyle {frac {1pm {sqrt {5}}}{2}}{frac {b}{b}}}}{{frac {c}{b}}}}}}}}}}where c=a+b; aterio0; bì0; b
bb=ac{displaystyle bb=ac}
b2=ac{displaystyle b^{2}=ac}
b2=a↓ ↓ (a+b){displaystyle b^{2}=a*(a+b)}
b2=a2+ab{displaystyle b^{2}=a^{2}+ab}
a2− − b2+ab=0{displaystyle a^{2}-b^{2}+ab=0}
Replacing the variables by pairs of consecutive values of the Fibonacci sequence (a=1;b=2 or a=3;b=5) it is seen that:
(1)2− − (2)2+(1)↓ ↓ (2)=− − 1{displaystyle (1)^{2}-(2)^{2}+(1)*(2)=-1}
(3)2− − (5)2+(3)↓ ↓ (5)=− − 1{displaystyle (3)^{2}-(5)^{2}+(3)*(5)=-1}
With the following formula you can establish how strong the golden relationship is between two numbers: 0 It is a perfect golden relationship and in the extremes 1 and - 1 are numbers belonging to the Fibonacci succession <math alttext="{displaystyle -1<=a^{2}-b^{2}+ab− − 1♫a2− − b2+ab♫1{displaystyle -1 habit=a^{2}-b^{2}+ab margin=1}<img alt="{displaystyle -1<=a^{2}-b^{2}+ab
Generating function
A generating function for any succession a0,a1,a2,...... {displaystyle a_{0},a_{1},a_{2},dots } is the function f(x)=a0+a1x+a2x2+a3x3+a4x4+ {displaystyle f(x)=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+cdots }, that is, a formal series of powers where each coefficient is an element of succession. Fibonacci numbers have the generator function
(4)f(x)=x1− − x− − x2{displaystyle fleft(xright)={frac {x}{1-x-x^{2}}}}}}}
When this function expands into powerpowers x{displaystyle x,}, the coefficients turn out to be Fibonacci's succession:
- x1− − x− − x2=0x0+1x1+1x2+2x3+3x4+5x5+8x6+13x7+ {displaystyle {frac {x}{1-x-x^{2}}}}=0x^{0}+1x^{1x^{2}+2x^{3}+3x^{4} +5x^{5}+8x^{6}+13x^{7}+cdots}
Explicit formula
The definition of the Fibonacci sequence is recursive; that is to say that all the previous terms need to be calculated in order to be able to calculate a specific term. An explicit formula of the Fibonacci sequence (which does not require calculating previous terms) can be obtained by noting that the equations (), () and () define the recurrence relation
- fn+2− − fn+1− − fn=0{displaystyle f_{n+2}-f_{n+1}-f_{n}=0,}
with initial conditions
- f0=0{displaystyle f_{0}=0,} and f1=1{displaystyle f_{1}=1,}
The polynomial characteristic of this relationship of recurrence is t2− − t− − 1=0{displaystyle t^{2}-t-1=0}, and its roots are
- t=1± ± 52{displaystyle t={frac {1pm {sqrt {5}}}{2}}}{2}}}}
In this way, the explicit formula of the Fibonacci sequence will have the form
- fn=b(1+52)n+d(1− − 52)n{displaystyle f_{n}=bleft({frac {1+{sqrt {5}}}}{2}right)^{n}+dleft({frac {1-{sqrt {5}}}{2}}{2}}{right)^{n}.
If the initial conditions are taken into account, then the constants b{displaystyle b} and d{displaystyle d} satisfy the previous equation when n=0{displaystyle n=0} and n=1{displaystyle n=1}, that is to say that they satisfy the system of equations
- b+d=0b(1+52)+d(1− − 52)=1!{displaystyle left.{begin{array}{rcl}b+d fake= fake0bleft({frac {1+{sqrt {5}}}}{2}}}}{2}}{right)+dleft({frac {1-{sqrt {5}{2}{2}}{2}}}{2}}{right}}}}}}}{right}}{right}{right}{end}{right}{
By solving this system of equations we get
- b=15,d=− − 15{displaystyle b={frac {1}{sqrt {5}}}}},d=-{frac {1}{sqrt {5}}}}}}}
Therefore, each number of the Fibonacci sequence can be expressed as
(5)fn=15(1+52)n− − 15(1− − 52)n{displaystyle f_{n}={frac {1}{sqrt {5}}}}{left({frac {1+{sqrt {5}}{2}}}{2}}}{n}-{frac {1}{sqrt {5}}}{1-{sqrt {1}{1}{1}{1}{1}{1}{1}{1}{1}{1}{sqf}}{1}}{1}{1}{1}{1}{s}{1}{f}}{f}}}}}{f}}}}}{f}}}}}}{f)}{1}}{
To simplify even more it is necessary to consider the golden number
- φ φ =1+52{displaystyle varphi ={frac {1+{sqrt {5}}}}{2}}}}}
so that the equation () reduces to
(6)fn=φ φ n− − (− − φ φ − − 1)n5{displaystyle f_{n}={frac {varphi ^{n}-left(-varphi ^{-1}right)^{n}}{sqrt {5}}}}}}}}}
This formula, known as Binet formula, is attributed to the French mathematician Édouard Lucas, and is easily demonstrable by mathematical induction. Although Fibonacci's succession consists only of natural numbers, its explicit formula includes the irrational number φ φ {displaystyle varphi ,}. In fact, the relationship with this number is narrow.
Noting the values adopted by the two sums of the formula (), it is verified that the second sum always has a lower absolute value than 1{displaystyle 1}, and it changes in sign successively, compensating the not whole, irrational part, which has the first sum, so that the sum of two irrational numbers gives a natural number.
Bearing in mind then that second sum of the formula () is always a number of absolute value less than 0.5{displaystyle 0.5}, (the maximum absolute value is for n=0{displaystyle n=0}, approximately 0.4472{displaystyle 0.4472}), the formula can be written, eliminating this second adding, like this:
(7)fn=int (15(1+52)n+12){displaystyle f_{n}=operatortorname {int} left({frac {1{sqrt {5}}}}}}{left({frac {1+{sqrt {5}}}}{2}}}{2}}{right)}{n}
or what is the same, using the golden number φ φ {displaystyle varphi }:
(8)fn=int (φ φ n5+12){displaystyle f_{n}=operatortorname {int} left({frac {varphi ^{n}{sqrt {5}}}}} +{frac {1}{2}}{2}}}{right)}
Matrix form
Another way to obtain the Fibonacci sequence is by considering the linear system of equations
- fn=fnfn− − 1+fn=fn+1!{displaystyle left.{begin{array}{rcl}f_{n} alien= fakef_{n}f_{n-1}+f_{n}{n}{n}{n+1}end{array}}}{right}}}
This system can be represented by its matrix notation as
- [chuckles]0111][chuckles]fn− − 1fn]=[chuckles]fnfn+1]{displaystyle {begin{bmatrix}0 fake1\1 fake1end{bmatrix}}{begin{bmatrix}f_{n-1}f_{n}end{bmatrix}}}}}{{begin{bmatrix}f_{n}f_{n+1end{bmatrix}}}}}}}}}}}}}}{bmatrix}}}}}}{bmatrix{bmatrix
Knowing f0=0{displaystyle f_{0}=0} and f1=1{displaystyle f_{1}=1}when applying the previous formula n{displaystyle n} times you get
(9)[chuckles]0111]n[chuckles]01]=[chuckles]fnfn+1]{displaystyle {begin{bmatrix}0 dream1\1 fake1end{bmatrix}}{n}{begin{bmatrix}01end{bmatrix}}}}}{{begin{bmatrix}f_{n}f_{n+1}end{bmatrix}}}}}}}}}}{{bmatrix}{bmatrix}}{bmatrix
Autovalores of the matrix [chuckles]0111]{displaystyle {begin{bmatrix}0 fake1{bmatrix}}}are precisely φ φ =1+52{displaystyle varphi ={frac {1+{sqrt {5}}}}{2}}}}} and END END =1− − 52{displaystyle psi ={frac {1-{sqrt {5}}}{2}}}{2}}}}(the golden number) φ φ {displaystyle varphi }and the negative of its reverse or conjugated END END =− − 1φ φ =1− − φ φ {displaystyle psi ={frac {-1}{varphi }}=1-varphi }); and its auto-voctors (END END ,− − 1){displaystyle (psi-1)} and (φ φ ,− − 1){displaystyle (varphi-1)}.
By applying techniques of spectral decomposition of the matrix, using its eigenvalues, and the base of its eigenvectors, or by diagonalizing the matrix, it is possible to substitute or simplify the operation of potentiation of the matrix, and obtain, by two other methods, the explicit formula () that gives the general term of the sequence.
Also checked
(10)[chuckles]0111]n=[chuckles]fn− − 1fnfnfn+1]{displaystyle {begin{bmatrix}0 fake11 fake1end{bmatrix}}{n}={begin{bmatrix}f_{n-1}{n}{n}{n}{n}{n}{n}{n}{n}{bmatrix}}}}}}}
This equality can be proved by mathematical induction.
Properties of the sequence
Fibonacci numbers appear in numerous applications from different areas. For example, in rabbit or plant breeding models, counting the number of bit strings in length n{displaystyle n} that have no consecutive zeros and a vast number of different contexts. In fact, there is a specialized publication called Fibonacci Quarterlydedicated to the study of the succession of Fibonacci and related topics. It is a tribute to the extent with which Fibonacci numbers appear in mathematics and their applications in other areas. Some of the properties of this succession are the following:
- The reason or quotient between a term and the immediately preceding one varies continuously, but it stabilizes in the golden number. I mean:
limn→ → ∞ ∞ fn+1fn=φ φ {displaystyle lim _{nto infty }{frac {f_{n+1}}{f_{n}}}}
- This limit is not deprived of the Fibonacci Succession. Any recurring succession of order 2, such as succession 3, 4, 7, 11, 18, leads to the same limit. This was demonstrated by Barr and Schooling in a letter published in the London magazine The Field December 14, 1912.[chuckles]required] The quotients are oscillating; that is, a quotient is less than the limit and the next is greater. The quotients can be ordered in two successions that approach asymptoically by excess and by default to the limit value.
- Any natural number can be written by adding a limited number of terms of Fibonacci succession, each of them different from the others. For example, 17=13+3+1{displaystyle 17=13+3+1}, 65=55+8+2{displaystyle 65=55+8+2}.
- Only one term of each three is pair, one in four is multiple of 3, one in five is multiple of 5, etc. This can be generalized, so that Fibonacci succession is periodic in module congruences m{displaystyle m}For any m{displaystyle m}.
- Succession can be expressed through another explicit formula called shape of Binet (from Jacques Binet). Yeah. α α =1+52{displaystyle textstyle alpha ={frac {1+{sqrt {5}}{2}}}}} and β β =1− − 52{displaystyle textstyle beta ={frac {1-{sqrt {5}}{2}}}}}, then
- fn=α α n− − β β nα α − − β β {displaystyle f_{n}={alphac {alpha ^{n}-beta ^{n}}{alpha-beta }}}} and fn≈ ≈ α α n5{displaystyle f_{n}approx {frac {alpha ^{n}{sqrt {5}}}{,}
- Each Fibonacci number is the average of the term that is two positions before and the term that is a position later. I mean
- fn=fn− − 2+fn+12{displaystyle f_{n}={frac {f_{n-2}+f_{n+1}}{2}}}{2}}}}
- The above can also be expressed as follows: calculating the next number to a given number is 2 times this number minus the number 2 positions further back.
- fn+1=fn↓ ↓ 2− − fn− − 2{displaystyle f_{n+1}=f_{n}*2-f_{n-2}
- The sum of the n{displaystyle n} first numbers is equal to the number that occupies the position n+2{displaystyle n+2} minus one. I mean
- f0+f1+f2+ +fn=fn+2− − 1{displaystyle f_{0}+f_{1}+f_{2}+cdots +f_{n}=f_{n+2}-1}
- Other interesting identities include the following:
- f0− − f1+f2− − +(− − 1)nfn=(− − 1)nfn− − 1− − 1{displaystyle f_{0}-f_{1}+f_{2}-cdots +(-1)^{nf_{n}=(-1)^{n}f_{n-1}-1}
- f1+f3+f5+ +f2n− − 1=f2n{displaystyle f_{1}+f_{3}+f_{5}+cdots +f_{2n-1}=f_{2n}}}
- f0+f2+f4+ +f2n=f2n+1− − 1{displaystyle f_{0}+f_{2}+f_{4}+cdots +f_{2n}=f_{2n+1}-1}
- f02+f12+f22+ +fn2=fnfn+1{displaystyle f_{0}{2}+f_{1}^{2}+f_{2}{2}{2}{2} +cdots +f_{n}{2}{2}=f_{n}f_{n+1}}}}
- f1f2+f2f3+f3f4+ +f2n− − 1f2n=f2n2{displaystyle f_{1}f_{2}+f_{2}f_{3}+f_{3}f_{4}f_{4}+cdots +f_{2n-1}f_{2n}=f_{2n}{2n}{2}{2}}
- f1f2+f2f3+f3f4+ +f2nf2n+1=f2n+12− − 1{displaystyle f_{1}f_{2}+f_{2}f_{3}+f_{3}f_{4}f_{4}+cdots +f_{2n}f_{2n+1}=f_{2n+1}{2n+1}
- Yeah. k≥ ≥ 1{displaystyle kgeq 1}, then fn+k=fkfn+1+fk− − 1fn{displaystyle f_{n+k}=f_{k}f_{n+1}+f_{k-1}f_{n},} for any n≥ ≥ 0{displaystyle ngeq 0}
- fn+1fn− − 1− − fn2=(− − 1)n{displaystyle f_{n+1}f_{n-1}-f_{n}^{2}=(-1)^{n}} (Identity of Cassini)
- fn+12+fn2=f2n+1{displaystyle f_{n+1}^{2}+f_{n}^{2}=f_{2n+}}
- fn+22− − fn+12=fnfn+3{displaystyle f_{n+2}^{2}-f_{n+1}^{2}=f_{n}f_{n+3}}}}
- fn+22− − fn2=f2n+2{displaystyle f_{n+2}^{2}-f_{n}^{2}=f_{2n+2}}}
- fn+23+fn+13− − fn3=f3n+3{displaystyle f_{n+2}^{3}+f_{n+1}^{3}-f_{n}^{3}=f_{3n+3}}}}{3}}}}}{3}}}
- fn=φ φ n+1− − (fn+1)φ φ {displaystyle f_{n}=varphi ^{n+1}-(f_{n+1}}varphi } (with φ = golden numberor, clearing f(n+1) and applying 1/φ = φ-1:
- fn+1=φ φ n+(1− − φ φ )fn{displaystyle f_{n+1}=varphi ^{n}+(1-varphi)f_{n}}
- The maximum common splitter of two Fibonacci numbers is another Fibonacci number. More specifically
- mcd(fn,fm)=fmcd(n,m){displaystyle mathrm {mcd} left(f_{n},f_{mright}=f_{mathrm {mcd} left(n,mright)}}}}}}}}
- This means that fn{displaystyle f_{n},} and fn+1{displaystyle f_{n+1},} are relative cousins and fk{displaystyle f_{k},} divides exactly to fnk{displaystyle f_{nk},}
- Fibonacci numbers appear when the diagonals of the triangle of Pascal are added. I mean, for anyone n≥ ≥ 0{displaystyle ngeq 0},
- fn+1=␡ ␡ j=0 n2 (n− − jj){displaystyle f_{n+1}=sum _{j=0}^{leftlfloor {frac {n}{2}}}{rightrfloor }{begin{pmatrix}n-jjend{pmatrix}}}}}}}}{
- and more
- f3n=␡ ␡ j=0n(nj)2jfj{displaystyle f_{3n}=sum _{j=0}{n}{begin{pmatrix}njend{pmatrix}}}2^{j}f_{j}}
- Yeah. fp=a{displaystyle f_{p}=a}, such that a{displaystyle a} It's a prime number, then. p{displaystyle p} is also a prime number, with one exception, f4=3{displaystyle f_{4}=3}3 is a prime number, but 4 is not.
- The infinite sum of the terms of succession fn10n{displaystyle textstyle {frac {f_{n}}{10^{n}}}} It's exactly 1089{displaystyle textstyle {frac {10}{89}}}}.
- The sum of ten consecutive Fibonacci numbers is always 11 times higher than the seventh number of the series.
- The last digit of each number is repeated periodically every 60 numbers. The last two, every 300; from there, repeat each 15× × 10n− − 1{displaystyle 15times 10^{n-1}} numbers.
- As the succession of Fibonacci arises from the sum of the diagonals of the triangle of Pascal. It can also be characterized by φ φ {displaystyle varphi } (the golden number) based on these sums. Representing the limit in the infinite of reason between the sums of the diagonal pairs of the triangle (f2n){displaystyle (f_{2n}}} and the sums of the unforeseen diagonals (f2n− − 1){displaystyle (f_{2n-1}}}in this way:
φ φ =limn→ → +∞ ∞ ((2n− − 10)+(2n− − 21)+(2n− − 32)+...+(nn− − 1)(2n− − 20)+(2n− − 31)+(2n− − 42)+...+(n− − 1n− − 1)){displaystyle varphi =displaystyle lim _{nto {+}infty {left({dfrac {{binom {2n-1}{bi}{binom}{2n-2}{1}{1}{2n-3}{2n}}{2n}}{binom}{n1}}{x1}{2}}{2nx1}}{2}}}}}{2nx1⁄2nx1st}}}}}{x1⁄2}}}{x1⁄2}}}{x1⁄2nx1st}}}{x1st}}}}{x1st}{x1st}{x1st)}{x1st}}}}}}{x1st or φ φ ≈ ≈ ␡ ␡ k=0n− − 1(2n− − 1− − kk)␡ ␡ k=0n− − 1(2n− − 2− − kk){displaystyle varphi ,approx {},{dfrac {displaystyle sum _{k=0}{n-1},displaystyle {binom {2n-1-k}{k}}}}{displaystyle sum _{k=0}^{n-1},displaystyle {binom {2n-2-k}{k}{
Generalization
The fundamental concept of Fibonacci succession is that each element is the sum of the previous two. In this sense succession can expand to the whole numbers as ...... ,− − 8,5,− − 3,2,− − 1,1,0,1,1,2,3,5,8,...... {displaystyle ldots-8,5,-3,2,-1,1,0,1,2,3,5,8,ldots } so that the sum of any two consecutive numbers is the next immediate. In order to define the negative indices of succession, it is clear fn− − 2{displaystyle f_{n-2},} of the equation () from where you get
- fn− − 2=fn− − fn− − 1{displaystyle f_{n-2}=f_{n}-f_{n-1},}
This way, f− − n=fn{displaystyle f_{-n}=f_{n},} Yeah. n{displaystyle n} It's odd and f− − n=− − fn{displaystyle f_{-n}=-f_{n},} Yeah. n{displaystyle n} It's a pair.
Succession can be expanded to the real numbers field by taking the actual part of the explicit formula (ecution () when n{displaystyle n} It's any real number. The resulting function
- f(x)=φ φ x− − # (π π x)φ φ − − x5{displaystyle f(x)={frac {varphi ^{x}-cos(pi x)varphi ^{-x}{sqrt {5}}}}}}}}}}}
has the same characteristics as the Fibonacci sequence:
- f(0)=0{displaystyle f(0)=0~}
- f(1)=1{displaystyle f(1)=1~}
- f(x)=f(x− − 1)+f(x− − 2){displaystyle f(x)=f(x-1)+f(x-2)~} for any real number x{displaystyle x}
One Generalized Fibonacci succession It's a succession. g0,g1,g2,...... {displaystyle g_{0},g_{1},g_{2},ldots } where
(11)gn=gn− − 1+gn− − 2{displaystyle g_{n}=g_{n-1}+g_{n-2},} for n=2,3,4,5,...... {displaystyle n=2,3,4,5,ldots }
That is, each element of a generalized Fibonacci sequence is the sum of the two previous ones, but it does not necessarily start at 0 and 1.
A very important generalized Fibonacci sequence is formed by the powers of the golden ratio.
- φ φ n=φ φ n− − 1+φ φ n− − 2{displaystyle varphi ^{n}=varphi ^{n-1}+varphi ^{n-2}}.
The importance of this sequence lies in the fact that it can be expanded directly to the set of real numbers.
- φ φ x=φ φ x− − 1+φ φ x− − 2{displaystyle varphi ^{x}=varphi ^{x-1}+varphi ^{x-2}}.
...and that of the complexes.
- φ φ z=φ φ z− − 1+φ φ z− − 2{displaystyle varphi ^{z}=varphi ^{z-1}+varphi ^{z-2}}.
A remarkable feature is that, if g0,g1,g2,...... {displaystyle g_{0},g_{1},g_{2},ldots } is a widespread Fibonacci succession, then
- gn=fn− − 1g0+fng1{displaystyle g_{n}=f_{n-1}g_{0}+f_{n}
For example, the equation () can be generalized to
- [chuckles]0111]n[chuckles]g0g1]=[chuckles]gngn+1]{displaystyle {begin{bmatrix}0 dream1\1 fake1end{bmatrix}}{n}{begin{bmatrix}g_{0}g_{1}end{bmatrix}}}{{begin{bmatrix}g_{n}g_{n+1}end{bmatrix}}}{bmatrix}}{bmatrix}}{bmatrix}{bmatrix}}{bmatrix}{bmatrix}{bmatrix}{bmatrix}{bmatrix}
This means that any calculation on a generalized Fibonacci sequence can be performed using Fibonacci numbers.
Lucas Sequence
An example of a generalized Fibonacci sequence is the Lucas sequence, described by the equations
- l0=2{displaystyle l_{0}=2~}
- l1=1{displaystyle l_{1}=1~
- ln=ln− − 1+ln− − 2{displaystyle l_{n}=l_{n-1}+l_{n-2}~ for n=2,3,4,5,...... {displaystyle n=2,3,4,5,ldots }
The Lucas sequence is very similar to the Fibonacci sequence and shares many of its characteristics. Some interesting properties include:
- The proportion between a number of Luke and his immediate successor approaches the golden number. I mean
- limn→ → ∞ ∞ ln+1ln=φ φ {displaystyle lim _{nto infty }{frac {l_{n+1}}{l_{n}}}}}{varphi }
- The explicit formula for Lucas' succession is
- ln=φ φ n+(− − φ φ )− − n{displaystyle l_{n}=varphi ^{n}+(-varphi)^{-n}}}
- The sum of the first n{displaystyle n} Lucas numbers is the number found in the position n+2{displaystyle n+2} minus one. I mean
- l0+l1+l2+ +ln=ln+2− − 1{displaystyle l_{0}+l_{1}+l_{2}+cdots +l_{n}=l_{n+2}-1}
- Any formula containing a Lucas number can be expressed in terms of Fibonacci numbers through equality
- ln=fn− − 1+fn+1{displaystyle l_{n}=f_{n-1}+f_{n+1}~}
- Any formula containing a Fibonacci number can be expressed in terms of Lucas numbers by equality
- fn=ln− − 1+ln+15{displaystyle f_{n}={frac {l_{n-1}+l_{n+1}}{5}}}}{5}}}
Calculation algorithms
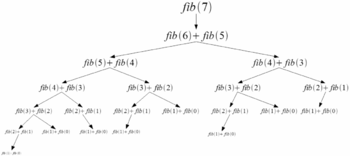
To calculate n{displaystyle n}-This is an element of Fibonacci succession. There are several algorithms (methods). Its definition itself can be used as one of these algorithms, here expressed in pseudocode:
| Algoritmo 1 Descending recursive version (Complexity) O(φ φ n){displaystyle O(varphi ^{n}),}) |
function fib(n){displaystyle {rm {fib}(n),}
|
Using algorithm analysis techniques it is possible to prove that, despite its simplicity, the algorithm required fn+1− − 1{displaystyle f_{n+1}-1} sums to find the result. Since the succession fn{displaystyle f_{n}} grows as fast as φ φ n{displaystyle varphi ^{n}}, then the algorithm is in order φ φ n{displaystyle varphi ^{n}}. I mean, this algorithm is very slow. For example, to calculate f50{displaystyle f_{50} this algorithm requires 20,365,011.073 sums.
To avoid doing so many operations, it is common to use a calculator and to use the equation () of the mathematician Édouard Lucas. However, since φ φ {displaystyle varphi } is an irrational number, the only way to use this formula is by using an approximation of φ φ {displaystyle varphi }, resulting in an approximate but not accurate result. For example, if a 10-digit calculator is used, then the previous formula throws as a result f50=1.258626903× × 1010{displaystyle f_{50}=1.258626903times 10^{10}} even though the correct result is f50=12586269025{displaystyle f_{50}=125869025}. This error becomes ever greater as it grows n{displaystyle n}. Similarly you can create a function using the formula, very efficient, O(log2 (n)){displaystyle O(log _{2}(n)}}}, although some considerations need to be taken into account, each programming language has a specific form of execution of mathematical functions, and it is likely that it will need to round the number obtained from the equation, and in certain cases, if the number is very large, it can be unpredictable.
| Algoritmo 2 Version with explicit formula ((Complexity) O(log2 (n)){displaystyle O(log _{2}(n)),}) |
function fib(n){displaystyle {rm {fib}(n),}
|
Another more practical method to recursion, which avoids calculating the same sums more than once, is iteration. Considering a pair (a,b){displaystyle (a,b,b)} of consecutive numbers of Fibonacci succession, the next pair of succession is (b,b+a){displaystyle (b,b+a),}, in this way an algorithm is seen where it is only required to consider two consecutive numbers of Fibonacci succession in each step. This method is the one that would normally be used to make the calculation with pencil and paper. The algorithm is expressed in pseudocode as:
|
|
|
These versions require only n{displaystyle n} amounts to be calculated fn{displaystyle f_{n}}, which means that iterative methods are considerably faster than the algorithm . For example, in the algorithm only 50 sums are required to calculate f50{displaystyle f_{50}.
An algorithm even faster is deducted from the equation (). Using exponent laws is possible to calculate xn{displaystyle x^{n}} Like
- xn={xYeah.n=1(xn2)2Yeah.nIt's a pair.x× × xn− − 1Yeah.nIt's odd.{displaystyle x^{n}={begin{cases}x fake{mbox{si }n}=1\left(x^{frac {n}{2}}{2}}{2}{2}{2}{mbox}{mbox{mbox{ is par}}{xxtimes x^{n-1case}{mbox{mbox{si}{si}{
In this way the Divide-type algorithm and Vencerás-type algorithm where it would only be required to do, approximately, log2 (n){displaystyle log _{2}(n)} matrix multiplications. However, it is not necessary to store the four values of each matrix since each one has the form
- [chuckles]abba+b]{displaystyle {begin{bmatrix}a blindb\b foolisha+bend{bmatrix}}}}}
In this way, each matrix is fully represented by the values a{displaystyle a} and b{displaystyle b}, and your square can be calculated as
- [chuckles]abba+b]2=[chuckles]a2+b2b(2a+b)b(2a+b)(a+b)2+b2]{displaystyle {begin{bmatrix}a fakeb\bbend{bmatrix}}}{2}={begin{bmatrix}a{2}+b{2}{2}{2}{2a+b}b(2a+b){2a+b){2}{2}+b^{2}end{bmatrix}
Therefore the algorithm is as follows:
| Algoritmo 6 Divide and Vencerás version (Complegety O(log2 (n)){displaystyle O(log _{2}(n)),}) |
function fib(n){displaystyle {rm {fib}(n),}
|
Despite how cumbersome it seems, this algorithm allows enormously reducing the number of operations needed to calculate very large Fibonacci numbers. For example, to calculate f100{displaystyle f_{100}instead of doing the 573.147.844.013.817.084.100 sums of the algorithm or the 100 sums with the algorithm , the calculation is reduced to just 9 matrix multiplications.
The Fibonacci sequence in nature
The Fibonacci sequence is found in multiple biological configurations, where consecutive numbers of the succession appear, such as the distribution of tree branches, the distribution of leaves on a stem, tropical pineapple fruits, the flowers of the artichoke, in the cones of the conifers, or in the "family tree" of honey bees. However, many unfounded claims to the appearance of the Fibonacci numbers have also been made, taking advantage of their relationship to the golden ratio in popular literature.
Przemysław Prusinkiewicz advanced the idea of considering the Fibonacci sequence in nature as a free group.
A model of the distribution pattern of sunflower seeds was proposed by H. Vogel in 1979. It presents the form
- θ θ =2π π φ φ 2n,r=cn{displaystyle theta ={frac {2pi }{phi ^{2}n, r=c{sqrt {n}}}}}
where n is the flower index and c is a scale factor; then the seeds are aligned according to Fermat spirals. The angle of divergence, approximately 137.51°, is related to the golden ratio. Because the coefficient is an irrational number, no seed has a neighbor at the same angle from the center, so they compact efficiently. Because rational approximations to the golden ratio are of the form F(j):F(j + 1), the nearest neighbors to seed number n are all in n ± F(j) for each index j, which depends on r, the distance to the center. It is often claimed that sunflowers and similar flowers have 55 spirals in one direction and 89 in the other (or some other pair of adjacent numbers in the Fibonacci sequence), but this is only true in certain ranges of radius, usually rare (and therefore this more notable).
The family tree of bees
The males of a bee hive have a family tree that complies with this sequence. The fact is that a drone (1), the male bee, does not have a father, but he does have a mother (1, 1), two grandparents, who are the parents of the queen (1, 1, 2), three great grandparents, since the queen's father has no father (1, 1, 2, 3), five great great grandparents (1, 1, 2, 3, 5), eight great great grandparents (1, 1, 2, 3, 5, 8) and so on, complying with the Fibonacci sequence.
Recently, a historical-mathematical analysis about the context of Leonardo of Pisa and the proximity of the city of Bejaia, an important wax exporter in Leonardo's time (from which the French name of this city comes, Bougie, meaning "candle"), has suggested that it was Bejaia's bee keepers and knowledge of bee ancestry that inspired the Fibonacci numbers rather than the rabbit breeding model.
Digits in the Fibonacci Sequence
One of the curiosities of this series are the digits of its elements:
- Starting in 1 digit and ending in in infinity, each digit value is shared by 4, 5 or 6 series numbers. Being 6 only in the case of 1 digit.
- In position elements n, n10, n100The number of digits increases in the same order. Giving multiple different for each n.
Divisibility
- Sean. n and more positive integers. If the number n It's divisible by m then the term n-simo of Fibonacci is divisible by the term m-simo of the same succession. In effect 4 divides to 12, therefore the term of order four, the 3 divides to 144, term of order 12 in the aforementioned succession.
- Whatever the whole mbetween m2− − 1{displaystyle m^{2}-1} First Fibonacci numbers will be at least one divisible per m. As an example for m = 4, the first fifteen numbers are 8 and 144, Fibonacci numbers, divisible by 4.
- Yeah. k is a different composite number of 4, then the k-simo number of Fibonacci is composed. For case 10, composed different from 4, the tenth number of Fibonacci 55, is composed.
- Fibonacci's consecutive numbers are cousins to each other.
The Fibonacci sequence in popular culture
- It is mentioned in the work of Rama II (novela), by Arthur C. Clarke, when the character Michael O'toole describes it as a reference to memorize a long secret key, mainly for its ease of being extrapolated.
Contenido relacionado
Nicolas Bourbaki
Coordinate system
Asymptote
























































































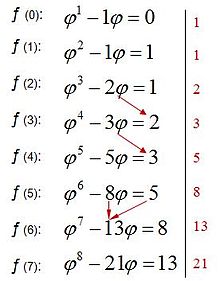

















































































![{displaystyle mathrm {vector} [0...n+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3a393bde03d0e8aa6c219359f5cfb1d28aa842b8)
![{displaystyle mathrm {vector} [0]gets 0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/faedc37ff5a1566f6db3d9f9ed8476a4e7b9dca6)
![{displaystyle mathrm {vector} [1]gets 1}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b15096b2b3daedff0b80b9f54b0d3ca8906b0984)


![{displaystyle mathrm {vector} [k]gets mathrm {vector} [k-1]+mathrm {vector} [k-2]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2b0713c9e95023fe4d8298f0fdc8df514160c972)
![{displaystyle mathrm {vector} [n],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/be28d66bce5ae0281652d423d77a2920f420176c)


























