Fibered

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

A cylindrical brush can give an intuitive idea of a vector fiber. The brush is like a vector fiber in which the base space is the cylinder where the fibers are stuck, while the wax fibers are interpretable segments like the mathematical fiber attached to each point. The application π:E→B I would take a point placed under a wax and apply all the fiber at the root of that wax on the cylinder.

In topology, a bundle (or bundle ) is a continuous function surjective π, from a topological space E into another topological space B, satisfying another condition that makes it particularly simple locally. Introducing another topological space F, we use the projection function of B × F → B as a model. For example, in the case of a vector bundle, F is a vector space.

Definition

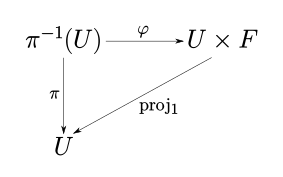
A fiber consists of a quarterna ${displaystyle (E,B,piF),}$ Where $E,$ , $B,$ and ${displaystyle F,}$ are topological spaces and ${displaystyle pi:Elongrightarrow B}$ is a continuous and over-yective application, so for any ${displaystyle xin B,}$ There is an environment ${displaystyle U,}$ of $x$ in ${displaystyle B,}$ and a homeomorphism ${displaystyle phi:pi ^{-1}(U)longrightarrow Utimes F,}$ such as ${displaystyle pi ={mbox{proj}}_{1}circ phi ,}$ , with ${displaystyle {mbox{proj}}_{1}:Utimes Flongrightarrow U}$ , ${displaystyle {mbox{proj}}_{1}(x,y)=x,}$ . Equivalently, for every point of B there is an environment $U$ and a homeomorphism $phi$ such that the following diagram conmutes:

Implementation $pi$ is open for being a projection in a cartesian product and B has the quotient topology. Space $B,$ It's called the base space of fiber, $E,$ the total spaceFor any ${displaystyle xin B,}$ , ${displaystyle pi ^{-1}(x),}$ It's called fiber in $x,$ and function ${displaystyle {mbox{proj}}_{1},}$ It's called the projection. It denotes ${displaystyle E|_{U}=pi ^{-1}(U)}$ and it is said that $pi$ That's it. locally trivial and the pair ${displaystyle (U,phi)}$ It's a local trivialization. It is usual to write $E$ instead of ${displaystyle (E,B,piF)}$ Yeah. ${displaystyle B,pi }$ and $F$ can be understood by context and say that E It's a fiber over B.

Examples

The first example is fiber product or trivial fiber given ${displaystyle (Btimes F,B,{mbox{proj}}_{1},F)}$ .

An example of non-globally trivial fiberdo is the Möbius Band as total space Ebase ${displaystyle Bcong S^{1}}$ a circle and fiber F=(0.1) a line segment. The rotation of segments F along the tape is appreciable only globally since locally the band structure is homeomorfa to a product ${displaystyle Utimes (0,1)}$ . An explicit analytical description is

${displaystyle E={frac {{(x,y)in mathbb {R} times (0,1)}}{(x,y)sim (x+1,1-y)}},quad Bcong S^{1}={frac {xin mathbb {R} }{xsim x+1}}}$

and implementation $pi$ is the projection in the first coordinate.

A vector fiber ${displaystyle (E,B,piF)}$ is in particular a fiberdo. The vector fiber is called Real or complex if the fiber F is a real vector space or complex respectively. Tangent fiber and cotangent fiber are examples of vector fibers.

A covering space or covering is a bundle, here the F is a discrete set.

There are in literature a wide range of examples with specific varieties or prescribed fibers. A couple of recurring examples in algebraic topology are Hopf Fibre ${displaystyle S^{2n+1}}$ on ${displaystyle mathbb {C} mathbb {P} ^{n}}$ fiber $S^1$ and the fiber of the path space of a topological space with base point ${displaystyle (X,x_{0})}$ , ${displaystyle {mathcal {P}}(X)longrightarrow X}$ with isomorph fiber to the bond space ${displaystyle Omega (X)}$ of $X$ .

Morphisms

A Morphism between two fibers ${displaystyle (E',B',pi ',F')}$ and ${displaystyle (E,B,piF)}$ consists of a pair of continuous applications ${displaystyle (f,{widetilde {f}})}$ , ${displaystyle f:B'longrightarrow B}$ and ${displaystyle {widetilde {f}}:E'longrightarrow E}$ , such that ${displaystyle {widetilde {f}}circ pi =pi 'f}$ . Note that implementation ${displaystyle {widetilde {f}}}$ determines the application $f$ . For each point ${displaystyle x'in B'}$ induces an application ${displaystyle {widetilde {f}}_{x}:E'_{x'}longrightarrow E_{f(x')}}$ .

Morphisms between fibers can be composed by ${displaystyle (f,{widetilde {f}})circ (g,{widetilde {g}}):=(fcirc g,{widetilde {f}}circ {widetilde {f}})}$ . In particular we have the notion isomorphism fiber: a morphism ${displaystyle (f,{widetilde {f}})}$ between two fibers ${displaystyle (E',B',pi ',F')}$ and ${displaystyle (E,B,piF)}$ It's a isomorphism if there is a morphism ${displaystyle (g,{widetilde {g}})}$ between ${displaystyle (E,B,piF)}$ and ${displaystyle (E',B',pi ',F')}$ such as ${displaystyle fcirc g=Id_{B},gcirc f=Id_{B'}}$ and ${displaystyle {widetilde {f}}circ {widetilde {g}}=Id_{E},{widetilde {g}}circ {widetilde {f}}=Id_{E'}}$ . Note that a necessary condition for fibers to be isomorphic is that fibers are isomorphic.

A vertical morphism in a fiber ${displaystyle (E,B,piF)}$ It's a morphism. ${displaystyle (f,{widetilde {f}})}$ with ${displaystyle f=Id_{B}}$ . A first step in the fiberd classification is to fix the base space B and classify base fibres B except isomorphism.

Operations

In this section we introduce possible operations in the category of bundles in topological spaces. For particular bundles it is possible to develop specific operations, for example the operations of linear algebra such as the dual space, the determinant, the tensor product and the outer product extends to the corresponding notions for vector bundles. The operations described here are general.

The pull-back fibers is one of the operations base change. Sea ${displaystyle (E,B,piF)}$ a fiber and ${displaystyle f:B'longrightarrow B}$ a continuous application. Fiber pull-back of E through f has total space

${displaystyle f^{*}E:={(x',e)in B'times E|f(x)=pi (e)}}$

with projection application ${displaystyle pi ':f^{*}Elongrightarrow B'}$ , ${displaystyle pi '(x',e)=x'}$ . So it's easy to prove that ${displaystyle (f^{*}E,B',pi ',F)}$ It's a fiber. Note that fibers $E$ and ${displaystyle f^{*}E}$ are isomorphs and there is a natural morphism of ${displaystyle f^{*}E}$ and $E$ . This operation is countervailing functorial with respect to the composition of morphosms, that is, ${displaystyle f^{*}(g^{*}E)=(gcirc f)^{*}E}$ and ${displaystyle id^{*}E=E}$ . Fiber pull-back depends in general on E and implementation f But yes. E It's a trivial fiber. ${displaystyle f^{*}E}$ too.

La restriction fibers. Sea ${displaystyle Asubset B}$ a subspace, ${displaystyle i:Alongrightarrow B}$ inclusion and E a fiber over B. Fiber restriction from E to subspace A is the fiber ${displaystyle i^{*}E}$ .

The product (cartesian) of two fibers ${displaystyle (E,B,piF)}$ and ${displaystyle (E',B',pi ',F')}$ It's fiber. ${displaystyle (Etimes E',Btimes B',pi times pi ',Ftimes F')}$ .

If E and E' are bundled on the same basis B, the product bundled on B is defined as

${displaystyle Etimes _{B}E':={(e,e')in Etimes E'|pi (e)=pi '(e')}longrightarrow B.}$

Fibers are therefore isomorphic to ${displaystyle Ftimes F'}$ . Note that the fiber ${displaystyle Etimes _{B}E'}$ is only the restriction of the cartesian fiber product to the diagonal ${displaystyle Delta _{B}subset Btimes B}$ with identification ${displaystyle Delta _{B}cong B}$ .

Homotopic properties

This section mentions properties of bundles in relation to homotopies. The proofs are exercises and can be found in any reference text.

The fundamental result to understand the behavior of fibers by homotopia is as follows: ${displaystyle Elongrightarrow Btimes [0,1]}$ a fiber and ${displaystyle pi _{1}:Btimes [0,1]longrightarrow B}$ the projection to the first factor, then ${displaystyle Econg pi _{1}^{*}left(E|_{Btimes {0}}right)}$ . In particular ${displaystyle E|_{Btimes {t}}cong left(E|_{Btimes {0}}times [0,1]right)|_{Btimes {t}}cong E|_{Btimes {0}}times {t}cong E|_{Btimes {0}}}$ .

Two corollaries follow from the previous statement:

(1) Sean ${displaystyle fsimeq g:B'longrightarrow B}$ continuous and homotopic applications and E a fiber over B. Then ${displaystyle f^{*}Econg g^{*}E.}$

(2) ${displaystyle r:Blongrightarrow Asubset B}$ a retract of deformation and E a fiber over B. So, ${displaystyle E|_{B}cong r^{*}(E|_{A}).}$

It deduces from the second result that if base space B is contractable any fiber ${displaystyle (E,B,piF)}$ isomorph to trivial fiber ${displaystyle Econg Btimes F}$ .

Sections

A section of a bundle is a continuous function, f: B → E such that π(f(x))=x, for x in B. In general, a bundle does not have sections, one of the purposes of the theory is to explain the existence of these as well as their quantification. Note that vector bundles always have a section, the zero section.

The obstruction to the existence of a section can be encoded in elements of a basis cohomology theory; in the case that the base space is a CW-complex, finding obstructions in cellular cohomology leads to the theory of feature classes in algebraic topology. A simple application of this theory is to show that spheres of even dimension do not have non-zero tangent fields, so they are not parallelizable.

Structural group

There is sometimes a topological group G of transformations of E, such that if ρ denotes the action, π (ρ(g)[e])= π(e) for g in G and e in E . The condition indicates that each G-orbit resides within a single fiber. In that case, G is called the structural group of the bundle. To qualify as G-bundled, the matching conditions between the local trivializable neighborhoods would have to be the intertwiners of G-shares as well.

If, in addition, G acts freely, transitively and continuously on each fiber, then we call the bundle main bundle. An example of a principal bundle that occurs naturally in geometry is the bundle of all bases of spaces tangent to a manifold, with G general linear group; the restriction in Riemann geometry to orthonormal bases would limit G to the orthogonal group. See vierbein for more details.

Making G explicit is essential to the operations of creating an associated bundle, and making precise reduction of the structural group of a bundle.

Applications

The language of bundle theory allows the expression of physical situations in mathematical terms. An instance of this is the gauge theories where the main bundles encode the physical notions of symmetries, potentials and force in terms of group structure, connections and curvature.

Contenido relacionado

Más resultados...