Fermat's number
A Fermat number, named after Pierre de Fermat, who formulated and investigated these numbers, is a natural number of the form:
- Fn=22n+1{displaystyle F_{n}=2^{2^{n}}+1}
where n is natural. Of particular interest are the Fermat primes.
Pierre de Fermat conjectured that all natural numbers of the form
- Fn=22n+1{displaystyle F_{n}=2^{2^{n}}+1}
with natural n were prime numbers (after all, the first five terms, 3 (n=0), 5 (n =1), 17 (n=2), 257 (n=3) and 65537 (n=4) are), but Leonhard Euler proved that this was not the case in 1732. Indeed, by taking n=5, a composite number is obtained:
- F5=225+1=232+1=4294967297=641× × 6700417{displaystyle F_{5}=2^{2^{5}}+1=2^{32}+1=4294967297=641times 6 700 417;}
- 4294967297 is the smallest number that, being Fermat number, is not a cousin.
Currently, only five Fermat prime numbers are known, which are the ones that were already known in the time of Fermat himself, and, as of January 2009, only the complete factorization of the first twelve Fermat numbers is known (since n=0 to n=11). These are some of the conjectures that exist today about these numbers:
- Is there only five prime numbers of Fermat (3, 5, 17, 257 and 65537)?
- Are there infinite cousins of Fermat?
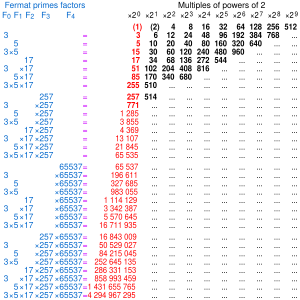
Some Fermat numbers and their factorization
The first nine Fermat numbers are as follows:
| F0 | = | 21 | + | 1 | = | 3 | |
| F1 | = | 22 | + | 1 | = | 5 | |
| F2 | = | 24 | + | 1 | = | 17 | |
| F3 | = | 28 | + | 1 | = | 257 | |
| F4 | = | 216 | + | 1 | = | 65.537 | |
| F5 | = | 232 | + | 1 | = | 4.294.967.297 | |
| = | 641 × 6.700.417 | ||||||
| F6 | = | 264 | + | 1 | = | 18.446.744.073.709.551.617 | |
| = | 274.177 × 67.280.421.310.721 | ||||||
| F7 | = | 2128 | + | 1 | = | 340.282.366.920.938.463.374.607.431.768.211.457 | |
| = | 59.649.589.127.497.217 × 5.704.689.200.685.129.054.721 | ||||||
| F8 | = | 2256 | + | 1 | = | 115.792.089.237.316.195.423.570.985.008.687.907.853.269.984.665.640.564.039.457.584.007.913.129.639.937 | |
| = | 1.238.926.361.552.897 × 93.461.639.715.357.977.769.163.558.199.606.896.584.051.237.541.638.188.580.280.321 |
Properties of Fermat numbers
- A Fermat number is equal to the product of all previous ones plus 2. This can be demonstrated by induction as follows:
- Yeah. n=1, it's true: F1 = F0 + 2 (5 = 3 + 2).
- If it is fulfilled k equal to n-1, it is fulfilled n:
| F0⋅ ⋅ F1⋅ ⋅ ...... ⋅ ⋅ Fn− − 2⋅ ⋅ Fn− − 1+2=(Fn− − 1− − 2)⋅ ⋅ Fn− − 1+2{displaystyle F_{0}cdot F_{1}cdot ldots cdot F_{n-2}cdot F_{n-1}+2=left(F_{n-1}-2right)cdot F_{n-1}+2,!} |
| =(22n− − 1+1− − 2)⋅ ⋅ (22n− − 1+1)+2{displaystyle =left(2^{2^{n-1}}+1-2right)cdot left(2^{2^{n-1}}}+1right)+2,!} |
| =(22n− − 1− − 1)⋅ ⋅ (22n− − 1+1)+2{displaystyle =left(2^{2^{n-1}}}-1right)cdot left(2^{2^{n-1}}+1right)+2,!} |
| =(22n− − 1)2− − 1+2=22n+1=Fn{displaystyle =left(2^{2^{n-1}}right)^{2}-1+2=2^{2^{n}} +1=F_{n},!} |
- Corolary of the previous property: No Fermat number can be the sum of two prime numbers. As all Fermat numbers are odd, one of the sums should be 2. Then the other will have to be, or 1 (in the case of F0 = 3) or the product of all previous ones... but precisely because it is a product of natural numbers it cannot be a cousin.
- Two different Fermat numbers are always cousins to each other (i.e., they have no common factor). You know that Fn = F0·F1·... ·Fn-1 + 2. Since all Fermat numbers are odd (and therefore 2 cannot be a common factor), it is concluded that Fn is not divisible by any of the factors of the previous Fermat numbers. A corollary of this is a demonstration of the infinity of the prime numbers (see article).
- Carl Friedrich Gauss showed that there is a relationship between the construction of regular polygons with rule and compass and the prime numbers of Fermat: a regular polygon n sides can be built with rule and beat if and only if n is either a power of 2, or the product of a power of 2 and different cousins of Fermat.
- All number composed of Fermat Fn=22n+1{displaystyle F_{n}=2^{2^{n}}+1} can be broken down into prime factors of form k·2n+2 + 1, with k positive integer.
- The hexadecimal representation of a larger Fermat number is especially simple: for each n greater than 2, Fn = 10...01Hexwhere there are 2n-2 - 1 zeros.
Relation to constructible polygons
Carl Friedrich Gauss developed the theory of Gaussian periods in his work Disquisitiones arithmeticae and formulated a sufficient one for the constructibility of regular polygons. He claimed that this condition was also necessary, but never published proof. Pierre Wantzel gave a complete proof of necessity in 1837. The result is known as the Gauss-Wantzel Theorem:
- A regular polygon can be built n side with rule and beat if and only if n is the product of a power of 2 and different cousins of Fermat: in other words, yes and only if n is shape n = 2kp1p2...psWhere k, s are non-negative integers and pi They are different cousins of Fermat.
A positive integer n has the above form if and only if its totinent φ(n) is a power of 2.
Applications of Fermat numbers
Generation of pseudorandom numbers
Fermat primes are particularly useful for generating pseudorandom sequences of numbers in the range 1... N, where N is a power of 2. The method The most common used is to take any seed value between 1 and P − 1, where P is a Fermat prime. Now, this value is multiplied by a number A, which is greater than the square root of P and is a primitive root modulo P (i.e. that is, it is not a quadratic residue). Then, the result is taken modulo P. The result is the new value for the pseudorandom number generator:
- Vj+1=(A× × Vj)modP{displaystyle V_{j+1}=(Atimes V_{j}){bmod {P}}}} (see Congruential Linear Generator, RANDU)
This is useful in computing, since most data structures have members with possible values 2X. For example, a byte has 256 (28) possible values (0–255). Therefore, to fill a byte or bytes with random values, one can use a random number generator that produces values from 1 to 256, with the byte taking the output value −1. Very large Fermat primes are of particular interest in data encryption for this reason. This method produces only pseudorandom values, since after P − 1 iterations, the sequence repeats. A poorly chosen multiplier can cause the sequence to repeat before P − 1.
Contenido relacionado
Zero divisor
Mathematical equality
Set