Excircle

An excircle of a triangle is a circle tangent to one of the sides of the triangle and to the extensions of the other two.

The center of the exincircle is called the exincenter. Three exincircles can be drawn for each triangle.

Definition

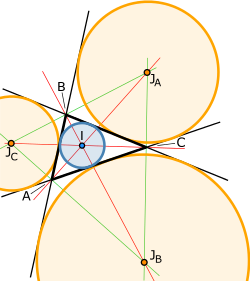
Let ABC be a triangle (in green in the figure). Let us draw its sides, considered as lines (in black). The inner and outer bisectors (in red) intersect at four points: one is the center of the inscribed circle (in brown), and the others are centers of the exinscribed circles (in yellow). The latter are "registered" in the sense that they are simultaneously tangent to the three sides, and are outside the triangle, hence their name.

To prove that two exterior bisectors of two angles of a triangle and the internal bisector of the third angle concur, let's take, for example, the interior bisector at A and the exterior bisectors at B and C:

• First we find that they cannot be parallel, because the sides of the triangle are not parallel.
• Secondly, consider the intersection of the two bisectrices from B and C. This point, A', is by equidistant definition of the sides (A')B) and (CBon the one hand, and (A)C) and (BC) on the other, therefore is equidistant of (CA) and (BA), then it belongs to a bisectr coming from A. It cannot be the external bisectr that is outside the BAC angular sector while A' is inside, therefore it is the internal bisectr.

Because of the above, point A' is equidistant from the three sides (AB), (AC) and (BC). Let d be this common distance. So the center circle A' and of radius d is tangent to the three sides of triangle ABC.

Properties

• An exinscribed circumference is on the outside of a triangle, except the point of tangence that belongs exactly. to one of the sides of the triangle.

• External and internal bisectrices are normal with each other.
• Exscript circles and the inscribed circumference are called tritangent circumferences to the triangle.
• The inner bisectrices are the heights of the triangle A'B'C' in the previous figure, which allows to find the initial triangle from the three exinscribed circles.

Spokes

The following is the value of the radius of each excircle:

• ra=p(p− − b)(p− − c)p− − a{displaystyle r_{a}={sqrt {frac {p(p-b)}{p-a}}}}}}}}

• rb=p(p− − a)(p− − c)p− − b{displaystyle r_{b}={sqrt {frac {p(p-a)}{p-b}}}}}}}}

• rc=p(p− − b)(p− − a)p− − c{displaystyle r_{c}={sqrt {frac {p(p-b)}{p-c}}}}}}}

Former Center

The exincenter is the center of an exincircle; is the intersection of the bisectors of any two of the three exterior angles and the interior bisector of the opposite angle of the tangent side of a triangle. Every triangle has three exincenters, one at the infinite exterior trapezoid of each side.

The inscribed circumference and the three exinscribed circles drawn from the exincentres.

From it, you can draw a circle that is tangent to one side and the extension of the other two.

As a consequence of the fact that the circumference is tangent to the extensions of the sides, the greatest distance from the vertex to the points of tangency are equal and added together they are equivalent to the perimeter of the triangle.

Features

• The exincenter is always outside the triangle.
• The exincenter is the centre of the circumference.
• It also passes through the exincenter the opposite internal bisectr next to which the exinscribed circumference is tangent.