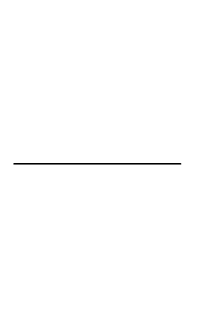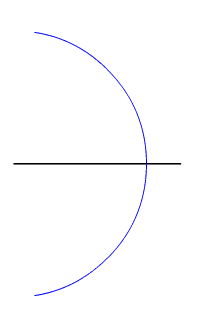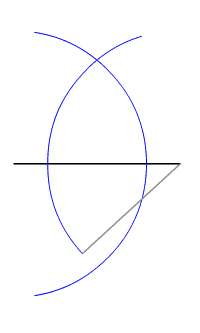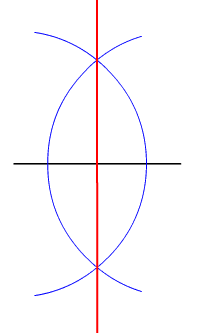Equidistant

Construction of the mediatrix of a straight segment. The point where the red line crosses the black segment is equidistant from both ends of this.

Polygon P is enrolled in circumference C. Circle O is equidistant from each point of the circumference, and therefore to every vertex of the polygon.

A point is said to be equidistant from a set of geometric figures if the distances between that point and each figure in the set are equal.

Generalization

In Euclidean geometry there are the following cases:

• In the line, it is known as midpoint to the point that is at the same distance or equidistant to two given or extreme points of a given segment.

• In aphin geometry, given the points A{displaystyle A} and B{displaystyle B} the midpoint is the midway point between A{displaystyle A} and B{displaystyle B}I mean, Pm=A+AB→ → 2=A+B2− − A2=A2+B2.{displaystyle P_{m}=A+{frac {vec {AB}}}{2}}=A+{frac {B}{2}}}-{frac {A}{2}}}}{frac {A}{2}}}+{frac {B}{2}}}}}}. !

On the plane

1. The mediatrix points of a segment are equidistant from the end of the segment.
2. The points of the circumference are equidistant from the center of the circumference.
3. The points of the bisectriz at an angle on the sides of this.
4. The points that match two parallel straights is a third parallel that is inside.
5. The points of the parable equidistan from the focus and the guideline.

• In space, the geometrical place of two-point equidistant points is a plane.
• In a dimension space (n), the geometric place of the two-point equidistant points is a hyperplane that is to say dimension (n− − 1).{displaystyle (n-1). !

Cases

Circumferences (set of equidistant points of one given) in the geometry of the discreet and continuous taxi driver.

Euclidean geometry

For a triangle, the center of the circumcircle is a point equidistant from each of the three vertices. Every non-degenerate triangle has such a point. Similarly, the incenter of a triangle or any other tangential polygon is equidistant from the points of tangency of the sides of the polygon with the circumference. Each point on the perpendicular bisector of a triangle or other polygon is equidistant from the two vertices at the endpoints of that side. Each point on the bisector of any polygon is equidistant from the two sides that confine that angle.

The center of a rectangle is equidistant from all four vertices, and it is equidistant from two opposite sides. A point on the axis of symmetry of a deltoid is equidistant between two of its sides.

The center of a circle is equidistant from every point on its perimeter. Similarly, the center of a sphere is equidistant from all points on its surface.

A parabola is the set of points in a plane that are equidistant from a fixed point (the focus) and a fixed line (the directrix).

In shape analysis, the calculation of the skeleton or middle axis of a figure is a linear version of that shape that is equidistant from its outline.

In Euclidean geometry, parallels (lines that never intersect) are equidistant in the sense that the distance of any point on one line from the nearest point on the other line is the same for all points.

Hyperbolic Geometry

In hyperbolic geometry, the set of points that are equidistant from and to one side of a given line form a hyperbolic circle (they have the arrangement of a curve, not a line, as in Euclidean space).

Other metrics

The concept of distance depends on the metric with which the relationship between the elements that form part of a topological space has been defined. In addition to the usual metric of Euclidean, ellipsoidal or hyperbolic spaces, there are other metrics (such as the one defined by the geometry of the taxi driver) in which, when applying the concept of equidistance, very different results are obtained from those intuitively expected. from the Euclidean intuition of geometry.