Ellipse
An ellipse is a flat, simple, closed curve with two axes of symmetry that results from cutting the surface of a cone by a plane oblique to the axis of symmetry with an angle greater than that of the generatrix with respect to the axis of revolution. An ellipse that rotates about its minor axis produces an oblate spheroid, while an ellipse that rotates about its major axis produces an elongated spheroid. An ellipse is also the affine image of a circle.
|
History
The ellipse, as a geometric curve, was studied by Menecmus, investigated by Euclid, and its name is attributed to Apollonius of Pergamum. The focus and the directrix of the conic section of an ellipse were studied by Pappus. In 1602, Kepler believed that the orbit of Mars was oval, although he later discovered that it was an ellipse with the Sun at one focus. In fact, Kepler introduced the word "focus" and published his discovery in 1609. Halley, in 1705, showed that the comet that now bears his name traced an elliptical orbit around the Sun.
Elements of an ellipse
The ellipse is a flat and closed curve, symmetric with respect to two mutually perpendicular axes:
- The major semage (the segment C-a and
- The smaller semage (the segment C-b of the figure).
They measure half the major and minor axis respectively.
Foci of an ellipse
The foci of the ellipse are two points equidistant from the center, F1 and F2 at the major axis. The sum of the distances from any point P on the ellipse to the two foci is constant, and equal to the length of the major diameter (d(P,F1)+d(P,F2)=2a).
For convenience we will denote by PQ the distance between two points P and Q.
If F1 and F2 are two points in a plane, and 2a is a constant greater than the distance F1F2, a point P will lie on the ellipse if the relationship holds:
- PF1+PF2=2a{displaystyle PF_{1}+PF_{2}=2a,}
where a{displaystyle a,} is the measurement of the ellipse's larger semieje.
Axes of an ellipse
The major axis, 2a, is the greatest distance between two opposite points on the ellipse. The result of the sum of the distances from any point to the foci is constant and equals the major axis. The minor axis 2b, is the shortest distance between two opposite points of the ellipse. The axes of the ellipse are perpendicular to each other.
Eccentricity of an ellipse
The eccentricity ε (epsilon) of an ellipse is the ratio between its semi-focal distance (length of the segment that starts from the center of the ellipse and ends at one of its foci), named by the letter c, and its semi-major axis. Its value is between zero and one.
- ε ε =ca{displaystyle varepsilon ={frac {c}{a}}}} with (0≤ ≤ ε ε ≤ ≤ 1){displaystyle (0leq varepsilon leq 1)}
Given that c=a2− − b2{displaystyle c={sqrt {a^{2}-b^{2}}}}} also worth the relationship:
- ε ε =a2− − b2a2=1− − b2a2{displaystyle varepsilon ={sqrt {cfrac {a^{2}-b^{2}}}{a^{2}}}}}}{sqrt {1-{frac {b^{2}}{a^{2}}}}}}}{a}}}}
or the system:
{ε ε =cac=a2− − b2{displaystyle {begin{cases}varepsilon ={cfrac {c}{a}c}c={sqrt {a^{2}-b^{2}}}}}}}{end{cases}}}}}
Eccentricity indicates the shape of an ellipse; an ellipse will be more rounded the closer its eccentricity approaches zero. The traditional designation for eccentricity is the Greek letter ε called epsilon.
(The letter e should not be used to designate it, because it is reserved for the base of natural logarithms. See: number e.)
Angular eccentricity of an ellipse
Angular eccentricity α α {displaystyle alpha } is the angle for which the value of the trigonometric function breast agreed with eccentricity ε ε {displaystyle varepsilon }, this is:
- α α =without− − 1 (ε ε )=#− − 1 (ba)=2So...− − 1 (a− − ba+b);{displaystyle alpha =sin ^{-1}(varepsilon)=cos ^{-1}left({frac {b}{a}{a}}}}}{right)=2tan ^{{-1}left({sqrt {frac {a-b}{a-b}{a-b}}}}{a-b}}}}}}}}}}{right);right;right);right;right;right;,, right?
Ellipse constant
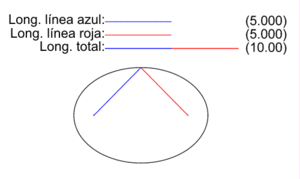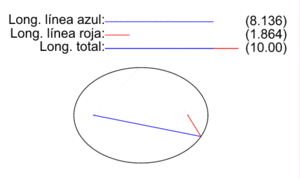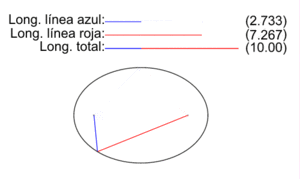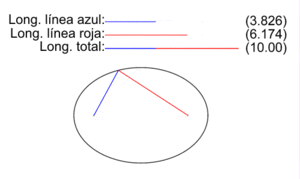
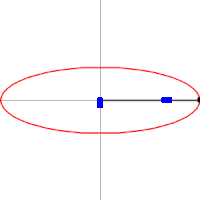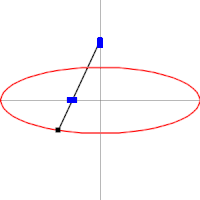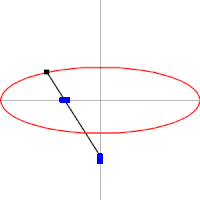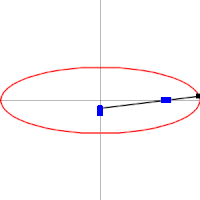
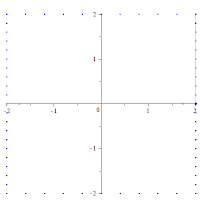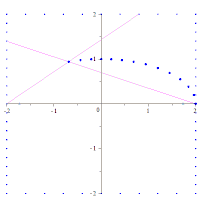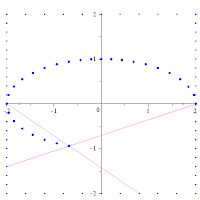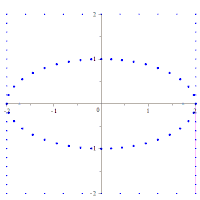
The figure on the right shows the two radio vectors corresponding to each point P of an ellipse, the vectors that go from the foci F1 and F2 to P. The lengths of the segments corresponding to each one are PF1 (blue color) and PF2 (red color).), and the animation illustrates how they vary for different points P of the ellipse.
As the initial definition of the ellipse as a locus establishes, for all points P of the ellipse the sum of the lengths of its two vector radii is a constant quantity equal to the length 2a of the major axis:
- PF1+PF2= 2a
The ellipse in image 2a is worth 10 and illustrates, for a select set of points, how the definition is fulfilled.
Ellipse Guidelines
Each focus F of the ellipse is associated with a line parallel to the semi-minor axis called the directrix (see illustration on the right). The distance from any point P on the ellipse to the focus F is a constant fraction of the perpendicular distance from that point P to the directrix that results in equality:
ε ε =PF! ! PD! ! {displaystyle varepsilon ={frac {overline {text{PF}}}{overline {text{PD}}}}}}}{displaystyle varepsilon
The relationship between these two distances is eccentricity ε ε {displaystyle varepsilon } from the ellipse. This property (which can be tested with the Dandelin sphere tool) can be taken as another alternative definition of the ellipse.
|
In addition to the well-known relationship ε ε =fa{displaystyle varepsilon ={frac {f}{a}}}}}It's also true that ε ε =ad{displaystyle varepsilon ={frac {a}{d}}}} the formula is also useful d=aε ε {displaystyle d={frac {a}{varepsilon }}}}.
Although only the directrix of the right focus was drawn in the figure, there is another directrix for the left focus whose distance from the center O is -d, which is also parallel to the previous directrix. See later how the directrix is drawn.
Ellipse graphic elements
Nomenclature
The description corresponds to the images on the right.
- Them main diameters or main axes are the maximum and minimum diameters of the ellipse, perpendicular to each other and passing through the center. They are traditionally appointed A-B the elder and D-C the minor, although other nomenclatures are also used, such as A-A' the elder and B-B' the minor.
- The center of the ellipse is usually named O (origin). In the circumference the focus coincides with the center.
- Them focus are usually named with the letter F accompanied by some means of differentiating them, F1 - F2or F' - F" .
- The diameter of the ellipse is usually designated 2a, being a the major semieje. The minor semieage is called b and diameter 2b. The distance of each focus to the center is called c.
- The segments that go from each focus to an ellipse point are called vector radios; the sum of the vector radios of each point is a constant equal to 2a.
In the image on the right we see some other important lines and points of the ellipse.
- La Main circumference (c. p., in green) has as its center the ellipse, and as a radio a. It can be defined as the geometric place of all the feet of the tangents to the ellipse (as seen in the example).
- The focal circles (c. f., in green also) are those that have as center each focus and as radius 2a. The focal circles and the main one fulfill a homotecia of reason = 2 and center in each focus (the one of the opposite focal circle).
- The straight t in cian color is a so. at any point. Al tangence point is usually named T, T1, T2etc. Perpendicular segments to tangents passing through the spotlights, here in red, are usually extended to the focal circle of the opposite focus. They do not match the normal to tangent except at the ends of the main axes.
- The points where normals cross with their tangents are the feet of tangent. That point always belongs to the main circumference. At double the distance from F to the foot is the cut of the normal with the focal circle of the opposite focus.
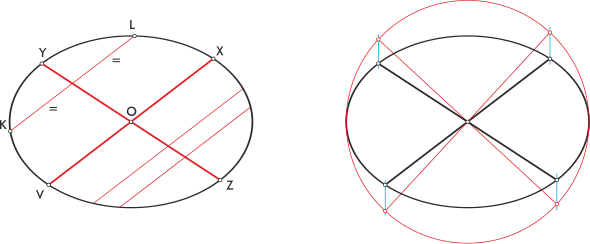
Conjugate diameters
The conjugate diameters are each pair of diameters of the ellipse whose one of them passes through the center of all the chords parallel to the other (see the drawing on the left below).
Another definition is that the diameters whose affines in a circumference affine to the ellipse are perpendicular are conjugate (drawing on the right).
The principal diameters would also be conjugate diameters. There are several methods to find the principal diameters from the conjugates.
Direct guidelines
The definition of the directive lines is in a previous section (see), and also the definition of the ellipse based on them. It is an expression of the eccentricity of the ellipse. The way to find them graphically is shown in the image on the right.
We draw a perpendicular to the major diameter through a focus up to the main circle, we draw a tangent to said circumference; in the place where that tangent meets the extension of the major diameter is the directrix, which is perpendicular to the major diameter.
Drawing the ellipse
Ellipse “of the gardener”
The method is based on the most common definition of the ellipse, as the locus of the points whose sum of distances to the foci is constant. The nails or thumbtacks are placed in the spotlights, and the string should be the same length as the major axis (2a). In the example of the photo, the distance of the lights must be added to the rope loop. With the taut string, the pencil or drawing material is moved completely surrounding the two bulbs.
This method is called “gardener's” because it is used to trace large ellipses on the ground with sufficient precision, with modest means. See in the next section how to determine the foci from the axes.
How to determine the foci
The way to determine the foci from the axes, or one axis from another and the foci, is based on the definition. Once the two main axes have been drawn, the measure a of the middle of the major axis is taken with the compass. Centering at one end of the minor axis, the compass crosses the major axis at the foci.
Given the major axis with the foci, the measure a applied to each focus gives us arcs that intersect at the ends of the minor axis.
Given a minor axis and the distance of the foci, we must first find the line on which the major axis lies, then draw the foci at the given distance, and from them take the distance to the endpoints of the minor axis, which is half the major axis.
Vector radius method
Also called "by points"; with this method we draw a sufficient number of points using the compass. As in the traditional method seen before, we use the radii vectors and the property that the sum of the radii vectors of a point is equal to the measure of the major axis.
Given two principal axes and the foci determined, random points are taken on the major axis between the center O and one of the foci. Generally three or four, and preferably near the focus for ease of drawing.
We take with the compass the distance from one end of the major axis (A) to each of the points of the axis (1). Making a center in each focus we draw arcs with that measurement. Next we take the rest of the measurement of the major axis, from point (1) to the other end (B), and with that measurement, centering again in the foci, we cross the arcs drawn before. The crosses give us points that belong to the ellipse.
By repeating the operation as many times as necessary, we obtain points of the ellipse. The drawing is completed by hand or by means of curve templates.
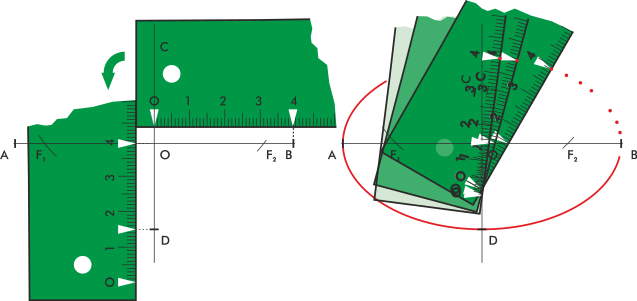
Card method, Archimedean compass
The ellipse can be drawn using a ruler, a set square and set square, and a pencil. We draw the main axes with their measures, and we determine the foci. We take with the graduated rule, from 0, the distance from the center to the end of the major axis, and then from the mark of the end of the major axis, we subtract half of the minor axis (see drawing). Supporting the 0 of the ruler at any point on the minor axis and the calculated difference on the major axis, we mark the measure of the major axis. For more clarity see the drawing.
This same operation can be done with a card, hence its traditional name, making marks on the edge with the given measurements.
To build it with rulers and compass we mark arbitrary points on the minor axis. Taking the measure of half the difference between the major and minor axis with the compass, we center the points and mark corresponding points on the major axis, on both sides. We draw lines from the points on the minor axis to their corresponding points on the major axis, extending them. On these straight lines, with the compass and from each point of the major axis, we take the measure of half of the minor axis, marking it on the line, which gives us the points of the ellipse.
There is a simple machine (an ellipsograph) made from guides or rails and bars and called Archimedean compass, which is based on this principle.
Affinity Construction
We start from the straight lines of the principal axes. Two concentric circles are drawn whose diameters are those of the ellipse. To find a point we draw any radius of the larger circle outside the axes. From the end of the radius we draw an auxiliary line, parallel to the minor axis, towards the inside of the circumference. From the point where the radius cuts the minor circumference we draw an auxiliary line parallel to the major axis, which crosses the auxiliary line that we have just made. The point where the two auxiliaries intersect belongs to the ellipse.
By repeating the operation, all the necessary points are obtained; the ellipse is completed by hand or with templates. Normally for convenience the drawing is systematized; instead of radii we draw full diameters, vertical and horizontal auxiliary strokes are made at once by parallels to the axes.
In this method, one of the circles can be considered as a double affine transformation of the other, and the points joined by the same radius would then be affine. One of the auxiliary lines is the line of affinity of two points (one on the circumference, the other on the ellipse), while the other auxiliary line gives the corresponding reduction
The relationship of the two circles can also be considered a homology in which the center of homology coincides with the center of a circle, while its homologous belongs to a parallel plane and is also concentric; these homologies with improper limit lines are dilations.
By affinity, from conjugates
From two conjugate diameters (A-B and C-D) the following construction can be made, in which we make the ends of the smaller conjugate diameter (C and C', the affinity line in blue) affine with that of an auxiliary circle with a diameter equal to the largest and perpendicular to it (in red), while the largest diameter is the axis of affinity. Each point on the circle is related to another point on the ellipse.
By affinity, inside a parallelogram
A common construction to draw an ellipse or an arc of an ellipse in a parallelogram is to make it similar to another orthogonal in which we can draw an arc of a circle or a complete circle. This is particularly useful for ellipses projected in axonometric or other cylindrical projection.
As seen in the drawing, we make two points are affine, as well as two lines that intersect in another that will act as the axis of affinity. The rest consists of transporting points and lines by means of other known related lines, normally the sides of the parallelograms or their diagonals (see the drawing).
The cube on the right shows the principle that is applied. It is important to note that in axonometric this procedure is not generally equivalent to a lowering.
By projective beams
Construction by projective beams, or the parallelogram. In the traditional variant we put as many points on the minor axis as on the sides of the rectangle parallel to the minor axis; we join these from the ends of the minor axis (C and D). Then we pass lines from those ends to the points of the major axis, until cutting the corresponding line. The crossing points belong to the ellipse.
In the second image we see the same procedure applied to two conjugate diameters; the rectangle becomes rhomboid, but the construction continues to function as a related projection of the other.
In another variant (see animated image) we draw points at equal distances, proportional side to side, in an outer rectangle tangent to the ellipse, which has the sides parallel to the minor axis of double size. We are joining each corresponding point in order as seen in the image, from the extremes to the major axis. The points that intersect the corresponding lines belong to the ellipse.
There are similar methods for drawing the parabola and the hyperbola.
The ellipse as a hypotrochoid
The ellipse is a particular case of a hypotrochoid, where R = 2r, where R is the radius of the directrix circle, and r the radius of the generating circle.
In a hypotrochoid curve, the circle that contains the generating point, rotates tangentially inside the directrix circle.
Anamorphosis of a circle into an ellipse
A certain transformation of the plane (by deforming the Cartesian plane) is called anamorphosis. The term anamorphosis comes from the Greek language and means to transform.
When transforming a circle or an ellipse by means of an affinity or a homology, the result is another ellipse (or a circle as a special case of ellipse).
 A circumference on an undeformed Cartesian plane. |  This circumference becomes an ellipse through an anamorphosis, where the Y-axis has been contracted and/or the X has dilated. |  Another modification of the container plane; the axes are not orthogonally deformed, but each point corresponds to another according to an improper center homology (affinity). |
 Another modification of the plane (homology) |  Another modification of the plane (free, on an ellipsoid) |
In the case of the circle, if the Cartesian plane is divided into a network of squares, when said plane is "deformed" in the direction of the X axis, the Y axis, or both, the circle becomes an ellipse and the squares into rectangles. This procedure was widely used to create illusionistic, anamorphic perspectives, called trompe l'oeil.
Equations of the ellipse
In Cartesian coordinates
Cartesian shape centered at the origin
The equation of an ellipse in Cartesian coordinates, with center at the origin, is:
x2a2+and2b2=1{displaystyle {frac {x^{2}}{a^{2}}}}}} +{frac {y^{2}{b^{2}}}}=1}
where a > 0 and b > 0 are the semiaxes of the ellipse, where if a corresponds to the x axis (abscissa) and b to the y axis (ordinate) the ellipse is horizontal, if it is the other way around, then it is vertical. The origin O is the midpoint of the segment [FF']. The distance between the spotlights FF' is called the focal length and is worth 2c = 2εa, where ε is the eccentricity and a is the semi-major axis.
Cartesian shape centered outside the origin
If the center of the ellipse is at the point (h,k){displaystyle (h,k)}The equation is:
(x− − h)2a2+(and− − k)2b2=1{displaystyle {frac {(x-h)^{2}}{a^{2}}}}{a^{2}}}}}{b^{2}}}}}{1}}
In polar coordinates
Polar form centered at origin
In polar coordinates, with origin at its center, the equation of the ellipse is:
(epc 1)r(θ θ )=1#2 θ θ a2+without2 θ θ b2{displaystyle r(theta)={frac {1}{sqrt {{cfrac {cos ^{2theta }{a^{2}}}}{cfrac {sin ^{2}{theta }{b^{2}}}}}}}}}}}}}
A more elegant equation than the previous one (but that forces pre-calculate eccentricity ε ε → → 1− − b2a2{displaystyle scriptstyle varepsilon to {sqrt {1-{frac {b^{2}}{a^{2}}}}}}}}), is:
(epc 2)r(θ θ )=b1− − ε ε 2#2 (θ θ ){displaystyle r(theta)={frac {b}{sqrt {1-varepsilon ^{2}cos ^{2}(theta)}}}}}}
For both equations a is the semimajor axis, b is the semiminor axis of the ellipse, θ is the polar angle and for the () ε is the eccentricity.
If you don't want to pre-calculate eccentricity ε ε → → 1− − b2a2{displaystyle scriptstyle varepsilon to {sqrt {1-{frac {b^{2}}{a^{2}}}}}}}} the equation should be used (), otherwise use the equation ().
Polar shapes centered on a focus
In polar coordinates, with the origin at focus F2, the equation of the ellipse is:
(501)r(θ θ )=a(1− − ε ε 2)1+ε ε # θ θ {displaystyle r(theta)={frac {a(1-varepsilon ^{2}}}{1+varepsilon cos theta }}}}}
For the F1 bulb:
(502)r(θ θ )=a(1− − ε ε 2)1− − ε ε # θ θ {displaystyle r(theta)={frac {a(1-varepsilon ^{2}}}{1-varepsilon cos theta }}}}}
In the case a little more general of an ellipse with the F2 focus on the origin and the other focus on the angular coordinate φ φ {displaystyle varphi }The polar shape is:
(503)r(θ θ )=a(1− − ε ε 2)1− − ε ε # (θ θ − − φ φ ){displaystyle r(theta)={frac {a(1-varepsilon ^{2}}}}{1-varepsilon cos(theta -varphi)}}}}}}}}}}
The angle θ θ {displaystyle theta } of the equations (),() and () is the call true abnormality of the point and the numberer of the same a(1− − ε ε 2){displaystyle a(1-varepsilon ^{2}}} It's the call. semi-latus rectum of the ellipse, normally denoted l{displaystyle l}. The semi-latus rectum is the distance between a focus and the same ellipse on a perpendicular line to the larger semieje passing through the focus.
Parametric shapes
Parametric equation of an ellipse with center in (h,k){displaystyle (h,k)} and being a{displaystyle a} the major semieje and b{displaystyle b} The minor is:
{x=h+a# α α and=k+bwithout α α {displaystyle {begin{cases}x=h+acos alpha \y=k+bsin alpha end{cases}}}}}
with α α 한 한 [chuckles]0,2π π ).α α {displaystyle alpha in [0.2pi). alpha } No. is the θ angle of the polar coordinate system originating in the center of the ellipse, but the eccentric anomaly of the ellipse. The relationship between α α {displaystyle alpha } and θ es
- tg θ θ =batg α α {displaystyle operatorname {tg} theta ={b over a}operatorname {tg} alpha }.
Parametric equation of an ellipse with center in (h,k){displaystyle (h,k)} in which the parameter θ θ {displaystyle theta } be consistent with the polar angle regarding the displaced center (h,k){displaystyle (h,k)} is:
{x=h+1# (θ θ )2a2+without (θ θ )2b2# θ θ and=k+1# (θ θ )2a2+without (θ θ )2b2without θ θ {displaystyle {begin{cases}x=h+{frac {1}{sqrt {{frac {{cos(theta){2}{a^{2}}{a^{2}}{cfrac}{cHFFFFFF}{cHFFFF}{cHFFFF}{cHFFFF}{cHFF}{cHFFFF}{cHFF}{cHFFFF}{cHFFFFFFFFFFFF}{cH00}{cHFFFFFFFFFFFFFFFFFF}{cHFFFFFF}{cHFF}{cHFF}{cH00}{cHFFFFFFFFFFFFFFFFFF}{cH00}{cHFFFF}{cHFF}{cHFFFF}{cHFF}{cHFFFFFFFFFFFFFFFFFF}{cHFF}{cHFFFFFF}{cH
with θ θ 한 한 [chuckles]0,2π π ){displaystyle theta in [0.2pi)}. The parameter θ θ {displaystyle theta } is the angle of a polar system whose origin is centered (h,k){displaystyle (h,k)}.
Curvature of an ellipse
K=ab(a2sen2 t+b2#2 t)32{displaystyle K={frac {ab}{(a^{2}{operatorname {sen} ^{2}t+b^{2}cos ^{2}t)^{frac {3}{2}{2}}}}}}}}}}
parameterized by
β β (t)=(a# t,bsen t){displaystyle beta (t)=(acos t,boperatorname {sen} t)}
and its curvature radius is R=1K{displaystyle R={frac {1}{K}}}}
Radius of curvature
Be the point M(x0,and0){displaystyle M(x_{0},y_{0}}}}} Then the curvature radius is
R=a2b2(x02a4+and02b4)1.5=(r1⋅ ⋅ r2)1.5ab{displaystyle R=a^{2}b^{2}({frac {x_{0}{2}}}}{a^{4}}}}}}{frac {y_{0}{2}}}}{b^{4}}}}}{1.5}={frac {(r_{1}cdot r_{2}{2}{2}}{1}{1}}{1}{1}{1}{1}}}{1⁄2}{1}{1}{1}}{1}{1}}{1⁄4}}{}}{1}{1}{}}{1}{1}{}{}{1}{1⁄4}{1}{}}{}{}{}{}{}{}{}{}{1}{}{}{}{}{}{}{}{}{}{}}{}}{
Area of the region enclosed by an ellipse
This region is determined by
x2a2+and2b2≤ ≤ 1{displaystyle {frac {x^{2}}{a^{2}}}}}} +{frac {y^{2}{b^{2}}}{1}}}{1}}}}}{leq 1}
In this case the searched area is:
A♪ ♪ rea=π π ⋅ ⋅ a⋅ ⋅ b{displaystyle {acute {A}rea=pi cdot acdot b}
Being a and b the semi-axes.
Perimeter of an ellipse
The calculation of the perimeter of an ellipse requires the calculation of elliptic integrals of the second kind.
However, the mathematician Ramanujan gave a simple expression that reasonably approximates the length of the ellipse, but to a lesser degree than that obtained by elliptic integrals. Ramanujan, in his formula, uses the "semi-major axis" (a) and the "semi-minor axis" (b) of the ellipse. Approximate expression of the perimeter of an ellipse:
- P≈ ≈ π π [chuckles]3(a+b)− − (3a+b)(a+3b)]{displaystyle Papprox pi left[3(a+b)-{sqrt {(3a+b)}}right]!,}
![{displaystyle Papprox pi left[3(a+b)-{sqrt {(3a+b)(a+3b)}}right]!,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/cc218b11158ffa2a1a3a03199f4fb0e7c63826cb)
Ellipse as conic
The ellipse is the intersection of a conical surface with a plane, in such a way that the inclination of the plane does not exceed the inclination of the generating line of the cone, thus making the intersection a simple closed curve. Otherwise the intersection could be a circle, a hyperbola or a parabola. That is why all these two-dimensional figures or plane curves are called conic sections or simply conics.
the ellipse as a conical.
Conical sections.
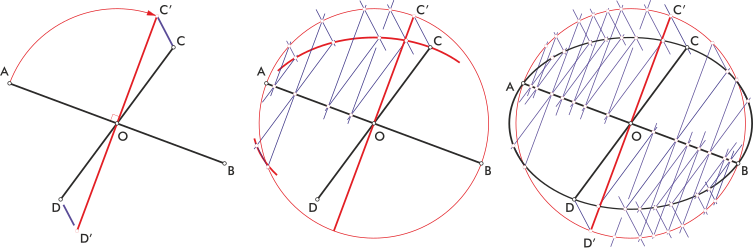
Similar ellipses
It is said that two figures are similar when they differ only in size (but not in shape), in such a way that multiplying all the lengths by a given factor, one passes from one figure to the other. There is a useful theorem in Physics about the intersection of a line with two similar and concentric ellipses.
|
Explanation: The theorem is true, due to symmetry, in the particular case in which the given ellipses are two concentric circles. By uniformly contracting or dilating one of the coordinate directions, through anamorphosis, we can transform any case into this particular case, since all segments with the same slope change their length in the same proportion. Therefore, since at the end of the process the two line segments have the same length, they already had it at the beginning.
Similar ellipses should not be confused with cofocal ellipses.
The ellipse in celestial mechanics
In classical celestial mechanics, two point masses subjected exclusively to gravitational interaction describe an elliptical (or circular) orbit around each other when the orbit is closed. An observer located in either of the masses will see that the other describes an ellipse one of whose foci (or center) is occupied by the observer himself. The eccentricity and other parameters of the trajectory depend, for two given masses, on the relative positions and velocities. The planets and the Sun satisfy the condition of point masses with great precision because their dimensions are much smaller than the distances between them. The kinematics of the orbit is governed by Kepler's laws.
The figure shows two different time intervals of an elliptical orbit that comply with Kepler's second law: "in equal times a mass in orbit sweeps out equal areas with its radius vector". When the "planet" is closer to the "star" it goes faster and when it is far away it goes slower, but in such a way that its areolar velocity is the same in both cases. This means that the areas of the yellow elliptical sectors are equal and their arcs t0 t1 have been traveled in equal time intervals, Δt = t1 - t0. The "star" is located at P, one of the foci of the ellipse.
The ellipse in everyday life
In a glass of water that is shaped like a right cylinder, when tilted, the surface of the water is shaped like an ellipse. In some metro stations with an elliptical plan, the conversation of some people who are close to the ellipse foci of the station can be heard in other parts of the enclosure as if the speakers were next door. This happens because the words are transmitted through the air by waves and arrive somewhere. There is a property of the ellipse that says that a line secant to an ellipse bounces in one of the points of intersection against it and passes through one of its two foci and that is what happens in subway stations.