Electromagnetism

Ferrofluid that is grouped near the poles of a powerful magnet.

Electromagnetism is the branch of physics that studies and unifies electrical and magnetic phenomena in a single theory. Electromagnetism describes the interaction of charged particles with electric and magnetic fields. Electromagnetic interaction is one of the four fundamental forces of the known universe. Charged particles interact electromagnetically by exchanging photons.

Electromagnetism encompasses various phenomena in the real world, such as light. Light is an oscillating electromagnetic field that radiates from accelerated charged particles. Apart from gravity, most of the forces in everyday experience are a consequence of electromagnetism.

The principles of electromagnetism find applications in various related disciplines, such as microwaves, antennas, electrical machines, satellite communications, bioelectromagnetism, plasmas, nuclear research, fiber optics, electromagnetic interference and compatibility, energy conversion electromechanics, radar meteorology, and remote sensing. Electromagnetic devices include transformers, relays, radio/TV, telephones, electric motors, transmission lines, waveguides, and lasers.

The foundations of electromagnetic theory were laid out by Michael Faraday and first fully formulated by James Clerk Maxwell in 1865. The formulation consists of four vector differential equations relating the electric field, magnetic field, and their respective sources materials (electric current, electric polarization and magnetic polarization), known as Maxwell's equations, which has been considered the "second great unification of physics", being the first made by Isaac Newton.

Electromagnetic theory can be divided into electrostatics—the study of the interactions between charges at rest—and electrodynamics—the study of the interactions between moving charges and radiation. The classical theory of electromagnetism is based on the Lorentz force and Maxwell's equations.

Electromagnetism is a field theory; that is, the explanations and predictions it provides are based on vector or tensor physical magnitudes dependent on the position in space and time. Electromagnetism describes the macroscopic physical phenomena in which electrical charges at rest and in motion intervene, using electric and magnetic fields and their effects on solid, liquid and gaseous substances. Because it is a macroscopic theory, that is, applicable to a very large number of particles and at large distances with respect to their dimensions, electromagnetism does not describe atomic and molecular phenomena. Quantum electrodynamics provides the quantum description of this interaction, which can be unified with the weak nuclear interaction according to the electroweak model.

History

This section is an extract from Electromagnetism History.[chuckles]edit]

Danish physicist Hans Christian Ørsted, performing the experiment that allowed him to discover the relationship between electricity and magnetism in 1820.

The history of electromagnetism, considered to be the knowledge and recorded use of electromagnetic forces, dates back more than two thousand years ago.

In ancient times they were already familiar with the effects of atmospheric electricity, particularly lightning, since storms are common in the southernmost latitudes, as the fire of San Telmo was also known. However, there was little understanding of electricity and they were not able to produce these phenomena.

During the seventeenth and eighteenth centuries, William Gilbert, Otto von Guericke, Stephen Gray, Benjamin Franklin, Alessandro Volta among others investigated these two phenomena separately and came to conclusions consistent with their experiments.

In the early 19th century, Hans Christian Ørsted found empirical evidence that magnetic and electrical phenomena were related. Hence the work of physicists like André-Marie Ampère, William Sturgeon, Joseph Henry, Georg Simon Ohm, Michael Faraday in that century, are unified by James Clerk Maxwell in 1861 with a set of equations that described both phenomena as one, as an electromagnetic phenomenon.

The now-called Maxwell equations showed that electric fields and magnetic fields were manifestations of a single electromagnetic field. In addition, he described the undulating nature of light, showing it as an electromagnetic wave. With a single consistent theory describing these two phenomena previously separated, the physicists were able to perform several prodigious experiments and very useful inventions such as the electric bulb by Thomas Alva Edison or the alternating current generator by Nikola Tesla. The predictive success of Maxwell's theory and the search for a coherent interpretation of his implications was what led Albert Einstein to formulate his relativity theory that was based on some previous results of Hendrik Antoon Lorentz and Henri Poincaré.

In the first half of the 20th century, with the advent of quantum mechanics, electromagnetism had to improve its formulation to be consistent with the new theory. This was achieved in the 1940s when an electromagnetic quantum theory known as quantum electrodynamics was completed.

History of the theory

Hans Christian Oersted

Originally, electricity and magnetism were considered two separate forces. This view changed, however, with the publication in 1873 of James Maxwell's Treatise on Electricity and Magnetism, which showed that the interaction of positive and negative charges is governed by a single force. There are four main effects, resulting from these interactions, which have been clearly demonstrated by experiments:

1. The electrical loads are drawn or repeld together with an inversely proportional force to the square of the distance between them: the different loads are attracted, the equal loads are repelled.
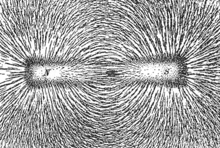
2. Magnetic poles (or polarization states in separate points) attract or repel each other in a similar way and always go in pairs: each north pole does not exist separately from the south pole.
3. The electric current in a cable creates a circular magnetic field around the cable, directed (in a time or anti-hour sense) according to the current flow.
4. A current is induced in the cable loop when it approaches or moves away from the magnetic field, or when the magnet approaches or moves away from the cable loop; the current direction depends on the direction of these movements.

André-Marie Ampere

In preparation for the conference, on the evening of April 21, 1820, Hans Christian Oersted made an astonishing observation. When he was compiling the material, he noticed that the compass needle deviated from the north magnetic pole when the electrical current from the battery he was using was turned on and off. This deviation led him to believe that magnetic fields emanate from all sides of a wire through which an electric current flows, just as light and heat propagate in space, and that experience indicates a direct connection between electricity and magnetism.

Michael Faraday

At the time of discovery, Oersted did not offer a satisfactory explanation of this phenomenon and did not attempt to present the phenomenon in mathematical calculations. However, three months later, he began to carry out more intensive investigations. Shortly after, he published the results of his research, showing that an electric current creates a magnetic field when it flows through wires. In the CGS system the unit of electromagnetic induction, Oe, received his name from his contribution to the field of electromagnetism.

James Clerk Maxwell

Oersted's conclusions led to intensive study of electrodynamics by the global scientific community. The works of Dominique François Arago also date back to 1820, who noticed that a wire through which an electric current flows attracts iron filings. He also magnetized iron and steel wires for the first time, placing them inside a coil of copper wires through which current passed. He also managed to magnetize the needle by placing it in a coil and discharging the Leyden Jar through the coil. Independently of Arago, Davy discovered the magnetization of steel and iron by current. The first quantitative definitions of the action of a current on a magnet in the same way date back to 1820 and belong to French scientists Jean-Baptiste Bio and Felix Savard. Oersted's experiments also influenced the French physicist André-Marie Ampere who He presented the electromagnetic law between a conductor and a current in mathematical form. Oersted's discovery also represents an important step towards a unified field concept.

This unit, which was discovered by Michael Faraday, completed by James Clerk Maxwell, and also refined by Oliver Heaviside and Heinrich Hertz, is one of the key achievements of the 19th century in mathematical physics. This discovery had far-reaching implications, one of which was understanding the nature of light. Light and other electromagnetic waves take the form of quantized self-propagating oscillatory phenomena of the electromagnetic field called photons. Different vibration frequencies lead to different forms of electromagnetic radiation: from radio waves at low frequencies, to visible light at medium frequencies, to gamma rays at high frequencies.

Oersted wasn't the only person to discover the connection between electricity and magnetism. In 1802, Giovanni Domenico Romagnosi, an Italian jurist, deflected a magnetic needle with electrostatic discharges. But in fact, Romagnosi's research did not use a galvanic cell and there was no direct current as such. The report of the discovery was published in 1802 in an Italian newspaper, but was hardly noticed by the scientific community at the time.

Branches

Electrostatics

Electrostatics is the study of phenomena associated with charged bodies at rest. As described by Coulomb's law, these bodies exert forces on each other. Its behavior can be analyzed in terms of the idea of an electric field surrounding any charged body, such that another charged body placed within the field will be subjected to a force proportional to the magnitude of its charge and the magnitude of the field at its location. Location. Whether the force is attractive or repulsive depends on the polarity of the charge. Electrostatics has many applications, ranging from the analysis of phenomena such as electrical storms to the study of the behavior of electronic tubes.

An electroscope used to measure the electrical load of an object.

When we talk about electrostatics we refer to the phenomena that occur due to an intrinsic and discrete property of matter, the charge, when it is stationary or does not depend on time. The unit of elementary charge, that is, the smallest observable, is the charge that the electron has. It is said that a body is electrically charged when it has an excess or lack of electrons in the atoms that compose it. By definition, the lack of electrons is called positive charge and the excess negative charge. The relationship between the two types of charge is attractive when they are different and repulsive when they are the same.

The elementary charge is a very small unit for practical calculations, so in the International System the unit of electric charge, the coulomb, is defined as the amount of charge transported in one second by a current of one ampere of intensity of electric current.

1C=1A⋅ ⋅ s{displaystyle 1 mathrm {C} =1 mathrm {A} cdot mathrm {s} }

which is equivalent to the charge of 6.25 x 10¹⁸ electrons. The movement of electrons through a conductor is called electric current and the amount of electric charge that passes per unit of time is defined like current intensity. More concepts such as potential difference or resistance can be introduced, which would inevitably lead us to the area of electrical circuits, and all of this can be seen in more detail in the main article.

The unit charge is named after Coulomb, who in 1785 arrived at a mathematical relationship of the electric force between point charges, now known as Coulomb's law:

F=14π π ε ε 0q1q2r2er{displaystyle mathbf {F} ={frac {1}{4pi varepsilon _{0}}}{frac {q_{1}q_{2}}}}{r^{2}}}}}{mathbf {e}{{{{r}}}}

Between two punctual loads q1{displaystyle q_{1};} and q2{displaystyle q_{2};} There is a force of attraction or repulsion F{displaystyle mathbf {F} } which varies according to the square of the distance r2{displaystyle r^{2};} and radial direction er{displaystyle mathbf {e} _{r}}and ε ε 0{displaystyle varepsilon} is a constant known as electric permitivity.

Elementary loads when not found alone should be treated as a distribution of them. That is why the concept of field, defined as a region of space where there is a scale or vector scale dependent or independent of time, should be implemented. So the electric field E→ → {displaystyle {vec {E}} is defined as the region of the space where the electric forces operate. Its intensity is defined as the limit to which the force of a load distribution tends on a positive charge that tends to zero, thus:

Electric field of punctual loads.

E=limΔ Δ q→ → 0FΔ Δ qΔ Δ q{displaystyle mathbf {E} =lim _{Delta qto 0}{frac {mathbf {F} _{Delta q}{Delta q}}}}}}}

And so we finally arrive at the mathematical expression that defines the electric field:

E=q4π π ε ε 0r2er{displaystyle mathbf {E} ={frac {q}{4pi varepsilon _{0}r^{2}}}}{mathbf {e}{{r}}}}}

It is important to know the scope of this concept of electric field: it gives us the opportunity to know what its intensity is and what happens to a charge in any part of said field regardless of the knowledge of what causes it.

One way to get what amount of power passes by a certain point or surface of the electric field is to use the concept of electric flow. This electric flow ≈ ≈ {displaystyle Phi } is defined as the sum of the amount of field that goes through a certain area, like this:

≈ ≈ =␡ ␡ E⋅ ⋅ Δ Δ S=♫ ♫ sE⋅ ⋅ dS{displaystyle Phi =sum mathbf {E} cdot Delta mathbf {S} =oint _{s}mathbf {E} cdot {text{d}}mathbf {S}} }

The mathematician and physical, Carl Friedrich Gauss, showed that the amount of electric flow in a field is equal to the quotient between the load enclosed by the surface in which the flow is calculated, qenc{displaystyle q_{enc};}and electric permitivity,ε ε 0{displaystyle varepsilon}. This relationship is known as the law of Gauss:

(1)≈ ≈ =♫ ♫ sE⋅ ⋅ dS=qencε ε 0{displaystyle Phi =oint _{s}mathbf {E} cdot {text{d}{mathbf {S} ={frac {q_{enc}}}{varepsilon _{0}}}}}}

Magnetostatics

Power lines from a magnetic bar.

The magnetosphere of the Earth, pushed by the solar wind.

It was only until the year of 1820, when Hans Christian Ørsted discovered that the magnetic phenomenon was linked to the electric, that a scientific theory was obtained for magnetism. The presence of an electrical current, that is, of a load flow due to a potential difference, generates a magnetic force that does not vary in time. If we have a load q at speed v{displaystyle mathbf {v} }in a magnetic field B{displaystyle mathbf {B} } A magnetic force induced by the movement will appear on this charge, as follows:

F=qv× × B{displaystyle mathbf {F} =qmathbf {v} times mathbf {B} }

To determine the value of that magnetic field, Jean Baptiste Biot in 1820, deduced a relationship for stationary currents, now known as the Biot-Savart law:

B=μ μ 0I4π π ♫ ♫ cdl× × rr3{displaystyle mathbf {B} ={frac {mu _{0}I}{4pi }}}{c}{frac {{text{d}}mathbf {l} times mathbf {r}}}{{{r^{3}}}}}}}

Where μ μ 0{displaystyle mu _{0},} is a proportionality coefficient known as magnetic permeability, I{displaystyle I,} is the current intensity, the dl{displaystyle {text{d}mathbf {l} } is the length differential by which the current circulates and r{displaystyle mathbf {r} } is the distance of this element of length the point where the magnetic induction is evaluated. Stricterly, B{displaystyle mathbf {B} } is the magnetic induction, said in other words, is the magnetic flow per unit area. Experimentally it was concluded that the magnetic field force lines were closed, eliminating the possibility of a magnetic monopole. The mathematical relationship is known as the law of Gauss for the magnetic field:

(2)♫ ♫ SB⋅ ⋅ dS=0{displaystyle oint _{S}mathbf {B} cdot {text{d}}mathbf {S} =0}

Furthermore, in magnetostatics there is a law comparable to Gauss's in electrostatics, Ampère's law. This law tells us that the circulation in a magnetic field is equal to the current density that exists in a closed surface:

♫ ♫ cB⋅ ⋅ dl=μ μ 0I{displaystyle oint _{c}mathbf {B} cdot {text{d}}mathbf {l} =mu _{0}I}

It should be noted that this Gauss law is a generalization of the Biot-Savart law. In addition to the fact that the formulas expressed here are for charges in a vacuum, for more information consult the main articles.

Classical Electrodynamics

Electrodynamics is the study of phenomena associated with moving charged bodies and variable electric and magnetic fields. Since a moving charge produces a magnetic field, electrodynamics refers to effects such as magnetism, electromagnetic radiation, and electromagnetic induction, including practical applications such as the electric generator and electric motor. This area of electrodynamics, known as classical electrodynamics, was systematically explained by James Clerk Maxwell, and Maxwell's equations describe the phenomena in this area with great generality. A more recently developed novelty is quantum electrodynamics, which incorporates the laws of quantum theory in order to explain the interaction of electromagnetic radiation with matter. Paul Dirac, Heisenberg and Wolfgang Pauli were pioneers in the formulation of quantum electrodynamics. Electrodynamics is inherently relativistic and gives corrections that are introduced into the description of the motions of charged particles when their velocities approach the speed of light. It applies to the phenomena involved with particle accelerators and with electronic tubes operating at high voltages and currents.

In previous sections, time-invariant electric and magnetic fields have been described. But physicists at the end of the 19th century discovered that both fields were linked and thus a moving electric field, an electric current that varies, generates a magnetic field, and a magnetic field itself implies the presence of an electric field. So, the first thing we must define is the force that a charged particle would have moving in a magnetic field and thus we arrive at the union of the two previous forces, what we know today as the Lorentz force:

(3)F=q(E+v× × B){displaystyle mathbf {F} =q(mathbf {E} +mathbf {v} times mathbf {B})}

Between 1890 and 1900 Liénard and Wiechert calculated the electromagnetic field associated with charges in arbitrary motion, a result known today as Liénard-Wiechert potentials.

On the other hand, to generate an electric current in a closed circuit there must be a potential difference between two points in the circuit, this potential difference is known as electromotive force or «emf». This electromotive force is proportional to the speed with which the magnetic flux varies in time, this law was found by Michael Faraday and is the interpretation of electromagnetic induction, thus a magnetic field that varies in time induces an electric field, a an electromotive force. Mathematically it is represented as:

(4)♫ ♫ CE⋅ ⋅ dl=− − ddt∫ ∫ SB⋅ ⋅ dS{displaystyle oint _{C}mathbf {E} cdot {text{d}}}mathbf {l} =-{frac {text{d}}}{{{{{text{d}}}}{int _{S}mathbf {B} cdot {text{d}{mathbf}}}}}{mathbf {

The physicist James Clerk Maxwell in 1861 related the aforementioned equations to Gauss's law ((1)), Gauss's law for the field magnetic ((2)), Faraday's law ((4)) and introduced the concept of a displacement current as an effective current density to arrive at the generalized Ampère's law (5):

(5)♫ ♫ CB⋅ ⋅ dl=μ μ 0∫ ∫ Sj⋅ ⋅ dS+μ μ 0ε ε 0ddt∫ ∫ SE⋅ ⋅ dS{displaystyle oint _{C}mathbf {B} cdot {text{d}}mathbf {l} =mu _{s}{s}{s}{s}{s}{s}{s}{s}{s}{s}{s}{s}{s}{s}{s} {s}}{s}{s}{s}{s}{s}{s}

The four equations, both in their differential and integral forms described here, are the result of the reformulation of Maxwell's work carried out by Oliver Heaviside and Heinrich Rudolf Hertz. But the real power of these equations, plus the Lorentz force (3), lies in the fact that together they are capable of describing any electromagnetic phenomenon, in addition to the physical consequences that will be described later.

An electromagnetic wave.

The genius of Maxwell's work is that his equations describe an electric field that is unequivocally linked to a magnetic field perpendicular to this and to the direction of its propagation, this field is now called an electromagnetic field. Such fields could be derived from a potential scale (φ φ {displaystyle phi }) and a vector potential (A{displaystyle mathbf {A} }) given by the equations:

(6)E=1c▪ ▪ A▪ ▪ t− − ► ► φ φ {displaystyle mathbf {E} ={frac {1}{c}}{frac {partial mathbf {A}{partial t}}-nabla phi }
B=► ► × × A{displaystyle mathbf {B} =nabla times mathbf {A} }

The solution of Maxwell's equations implied the existence of a wave that propagated at the speed of light, with which, in addition to unifying electrical and magnetic phenomena, the theory formulated by Maxwell predicted optical phenomena with absolute certainty.

Thus, the theory predicted a wave that, contrary to the ideas of the time, did not need a means of propagation; the electromagnetic wave could propagate in a vacuum due to the mutual generation of magnetic and electric fields. This wave, despite having a constant speed, the speed of light c, can have different wavelengths and consequently this wave carries energy. Electromagnetic radiation receives different names by varying its wavelength, such as gamma rays, X-rays, visible spectrum, etc.; but as a whole it is called the electromagnetic spectrum.

Relativistic Electrodynamics

Classically, by fixing a reference frame, you can decompose the electric and magnetic fields of the electromagnetic field. But, in the theory of special relativity, by having an observer with relative movement with respect to the reference system, he will measure different electrical and magnetic effects of the same electromagnetic phenomenon. The electric field and magnetic induction, despite being vector elements, do not behave as vector physical magnitudes, on the contrary, the union of both constitutes another physical entity called a tensor and in this case the electromagnetic field tensor.

Thus, the expression for the electromagnetic field is:

F=Fμ μ .. =(0Ex/cEand/cEz/c− − Ex/c0− − BzBand− − Eand/cBz0− − Bx− − Ez/c− − BandBx0){displaystyle mathbf {F} =F_{mu nu }={begin{pmatrix}0 fakeE_{x}/c nightmareE_{y}/c fake_{z}{b}{bc}{bcd}{x}{b_{z}{b_{y}{y}{Bend_{y}{bc}{bc}{bc}{bccc}{bcccccccccccccccccccccd)}{bnx}{bnx}{x}{bnx}{bnz}{x}{bnz}{x}{bccccccccccccccccccccccccccc

This representation is known as the four-dimensional covariant formulation of electromagnetism. Covariant expressions for Maxwell's equations (7) and the Lorentz force (6 ) are reduced to:

(6)fα α =␡ ␡ β β eFα α β β uβ β {displaystyle f_{alpha }=sum _{beta }e F_{alpha beta } u^{beta },}

(7)▪ ▪ μ μ Fμ μ .. =μ μ 0J.. {displaystyle partial _{mu }F^{mu nu }=mu _{0}J^{nu }}}▪ ▪ μ μ ⋅ ⋅ Fμ μ .. =0{displaystyle partial _{mu }cdot F^{mu nu }=0}

Given the form of the previous equations, if the domain over which the electromagnetic field extends is simply connected, the electromagnetic field can be expressed as the exterior derivative of a four-vector called vector potential, related to the potentials of classical electromagnetism of the Following way:

A=(A0;A1,A2,A3)=(φ φ ;A){displaystyle mathbf {A} =(A_{0};A_{1},A_{2},A_{3})=(phi;mathbf {A})}}

Where:

φ φ {displaystyle phi ;}It's the electrostatic potential.

A{displaystyle mathbf {A} }It's the classic vector potential.

The relationship between the four-vector potential and the electromagnetic field tensor turns out to be:

F=dA=12!▪ ▪ Aβ β ▪ ▪ xα α − − ▪ ▪ Aα α ▪ ▪ xβ β dxα α ∧ ∧ dxβ β =12!Fα α β β dxα α ∧ ∧ dxβ β {cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFFFF}{cHFFFFFFFF}{cHFFFFFFFF}{cH}{cHFFFFFF}{cHFFFFFF}{cH}{cHFFFFFFFFFFFFFFFFFF}{cH}{cH}{cH}{cH}{cHFFFFFFFF}{cHFFFFFFFFFFFFFFFFFFFFFF}{cH}{cH}{cHFFFFFFFF}{cHFFFF}{cHFFFFFFFFFFFFFFFF}{cH00}{cHFFFFFF}{cHFF}{cHFFFF}{cHFFFF}{cHFFFFFFFF}{cH}{cH}{cHFFFFFF}{cH

The fact that the electromagnetic interaction can be represented by a (quadri)vector that completely defines the electromagnetic field is the reason why it is affirmed in modern treatment that the electromagnetic interaction is a vector field.

In general relativity, the treatment of the electromagnetic field in a curved space-time is similar to that presented here for the Minkowski space-time, only that the partial derivatives with respect to the coordinates must be replaced by covariant derivatives.

Quantum Electrodynamics

Feynman diagram showing the electromagnetic force between two electrons through the exchange of a virtual photon.

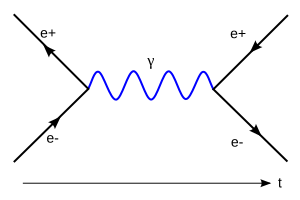
Following the quantum revolution of the early 20th century, physicists were forced to search for a quantum theory of electromagnetic interaction. Einstein's work with the photoelectric effect and the subsequent formulation of quantum mechanics suggested that electromagnetic interaction occurred through the exchange of elementary particles called photons. The new quantum formulation achieved in the 1940s describes the interaction between bosons, or particles carrying the interaction, and the other matter-carrying particles (fermions).

Quantum electrodynamics is primarily a renormalized quantum field theory. Its development was the work of Sinitiro Tomonaga, Julian Schwinger, Richard Feynman and Freeman Dyson around the years 1947 to 1949. In quantum electrodynamics, the interaction between particles is described by a Lagrangian that has local symmetry, specifically gauge symmetry. For quantum electrodynamics, the gauge field where the fermions interact is the electromagnetic field, described in this theory as the states of bosons (photons, in this case) carrying the interaction.

Mathematically, the Lagrangian for the interaction between fermions by exchanging photons is given by:

L=END END ! ! (iγ γ μ μ Dμ μ − − m)END END − − 14Fμ μ .. Fμ μ .. {displaystyle {mathcal {L}}={bar {psi }}(igamma ^{mu }D_{mu }-m)psi -{frac {1}{4}{4}}}F_{mu nu }F^{mu nu }

Where the meaning of the terms are:

γ γ μ μ {displaystyle gamma _{mu },!} It's Dirac's matrices.

END END {displaystyle psi } and END END ! ! {displaystyle {bar {psi}}} are the fields or thorns of Dirac that represent electrically charged particles.

Dμ μ =▪ ▪ μ μ +ieAμ μ {displaystyle D_{mu }=partial _{mu }+ieA_{mu },} is the covariant derivative associated with the gauge symmetry.

Aμ μ {displaystyle A_{mu}} the operator associated with the covariant vector potential of the electromagnetic field

Fμ μ .. =▪ ▪ μ μ A.. − − ▪ ▪ .. Aμ μ {displaystyle F_{mu nu }=partial _{mu }A_{nu }-partial _{nu }A_{mu },!} the field operator associated electromagnetic field tensor.

SI units of electromagnetism