Electrical capacity

In electromagnetism and electronics, electrical capacity is the property that bodies have to maintain an electric charge. Capacity is also a measure of the amount of electrical energy stored for a given electrical potential difference. The most common device that stores energy in this way is the capacitor. The relationship between the potential difference (or voltage) existing between the plates of the capacitor and the electrical charge stored in it, is described by the following mathematical expression:

C=qV{displaystyle {C}={q over V}}

where:

• C{displaystyle C,} is the capacity, measured in faradiums (in honor of the experimental physicist Michael Faraday); this unit is relatively large and used submultiplots such as micropharyadium or picopharyadium;
• q{displaystyle q,} is the electrical load stored, measured in assmbies;
• V{displaystyle V,} is the difference of potential (or voltage), measured in volts.

Note that capacitance is always a positive quantity and depends on the geometry of the capacitor (parallel plate, cylindrical, spherical). Another factor on which it depends is the dielectric that is introduced between the two surfaces of the capacitor. The higher the dielectric constant of the non-conductive material introduced, the higher the capacity.

In practice, the electrical dynamics of the capacitor is expressed thanks to the following differential equation, which is obtained by deriving the previous equation with respect to time.

I=dQdt=CdVdt{displaystyle {I}={frac {dQ}{dt}}}={C}{frac {dV}{dt}}}}}}}{

Where I represents electrical current, measured in amperes.

C=ε ε Ad{displaystyle C=varepsilon {frac {A}{d}}}}

Where:

C is capacity, in faradios;

A is the area of the plates, in square meters;

ε is permissibility;

d is the separation between the plates, in meters.

Stored energy

The energy stored in a capacitor, measured in July, is equal to work made to carry it. Consider a capacitor with a capacity Cwith a load +q on a plate and - Okay. on the other. To move a small amount of load dq{displaystyle mathrm {d} q} from one plate to the other in the opposite sense to the difference of potential a job must be done dW{displaystyle mathrm {d} W}:

dW=qCdq{displaystyle mathrm {d}

where

W is the work done, measured in July;

q is the burden, measured in coulombios;

C It is capacity, measured in faradios.

That is, to charge a capacitor, work must be done and part of this work is stored in the form of electrostatic potential energy. The energy stored in a capacitor can be calculated by integrating this equation. Starting with a discharged capacitor (q = 0) and moving charges from one plate to the other until they acquire charges +Q and -Q respectively, a W job must be done:

Wcarga=∫ ∫ 0QqCdq=12Q2C=12CV2=Walmacenada{displaystyle W_{charge}=int _{0}{Q}{frac {q}}}}{mathrm {d} q={frac {1}{2}}}{frac {Q^{2}}}}{C}{mathrm {d}{frac {1}}{frac {1}{2}}}}}}{frac {frac {Q}}}}{frac {Q}{frac {Q}{frac {Q}}{frac {Q}}}}}{fam {Q}}}}}}}}}}}}}}}}}}{fam {Q}}}}{fam {Q}}}}}}}}}}{fam {Q}}}}}}{fam {Q}}}}}}}{fam {fam}}}}}}}}}}}}}}}}}}}}}}}}}}{

Combining this expression with the equation above for capacity, we get:

Walmacenada=12CV2=12Q2C{displaystyle W_{almacenada}={frac {1}{2}}}CV^{2}={frac {1}{2}}{frac {Q^{2}}}{C}}}}}}{

where

• W is the energy, measured in July;
• C is the capacity, measured in faradios;
• V is the difference of potential, measured in volts;
• Q is the stored load, measured in coulombios.

Self-capacity

Usually the term mutual capacitance is used as an abbreviation for the term capacitance between two nearby conductors, such as the plates of a capacitor. However, for an insulated conductor there is also a property called self-capacitance, which is the amount of electric charge that must be added to an insulated conductor to increase its potential by one volt, in order to calculate the electric capacity through a parallel or flat capacitor. The theoretical reference point for this potential is a conducting hollow sphere of infinite radius centered on the conductor. Using this method, the self-capacitance of a conducting sphere of radius R is given by:

C=4π π ε ε 0R{displaystyle C=4pi varepsilon _{0}R,}

Here are some examples of auto-capacity values:

• For the "plate" of the top of a Van de Graaff generator, usually a 20 cm radius dial: 22.24 pF
• Planet Earth: about 710 μF

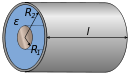
Capacitance of conductors with simple shapes

Calculating the capacitance of a system is equivalent to solving the Laplace equation ∇²φ = 0 with a constant potential φ at the two-dimensional surface of the conductors embedded in 3 spaces. This is simplified by the existence of symmetries. There is no solution in terms of elementary functions in more complicated cases.

For drawing situations, analytic functions can be used to perform the linkage between different geometries.

Training of simple systems

Type	Training	Commentary
Capacitor of parallel plates	ε ε A/d{displaystyle varepsilon A/d}	ε: Allowance or dielectric constant
Concentric cylinders	2π π ε ε l l ln (R2/R1){displaystyle {frac {2pi varepsilon ell }{ln left(R_{2}/R_{1}right)}}}}	ε: Allowance or dielectric constant
Eccentric cylinders	2π π ε ε l l archsh (R12+R22− − d22R1R2){displaystyle {frac {2pi varepsilon ell }{operatorname {arcosh} left({frac {R_{1}^{2}+R_{2}{2}{2}-d^{2}{2}}{2R_{1}R_{2}}}}{2}}}}}}}{2}}}{2}}}}}}}}}}}}}	ε: Allowance or dielectric constant R1: External radio R2: Internal radio dDistance between center l: longitu of the wire
Pair of parallel wires	π π ε ε l l archsh (d2a)=π π ε ε l l ln (d2a+d24a2− − 1){displaystyle {frac {pi varepsilon ell }{operatorname {arcosh} left({frac {d}{2a}}}{right}}}{frac {varepsilon}{ell }{ln left({frac}{2a}{2a}{sqrt {{c}{cn}{2}{cd}{cd}{}{cd}{}{cd}{cd}{cd}{cd}{cd}{cd}{cd}{}{cd}{cd}{cd}{}{}{
Wing parallel to a wall	2π π ε ε l l archsh (da)=2π π ε ε l l ln (da+d2a2− − 1){displaystyle {frac {2pi varepsilon ell }{operatorname {arcosh} left({frac {d}{a}}{right}}}{frac}{2pi varepsilon ell }{ln left({frac}{a}{a}{are}{c}{c}{	a: Wire radio d: Distance, d ▪ a l: long wire
Two parallel fajas coplanars	ε ε l l K(1− − k2)K(k){displaystyle varepsilon ell {frac {Kleft({sqrt {1-k^{2}right}}{Kleft(kright)}}}}}}}}}{Kleft(kright)}}}}	dDistance w1, w2: width of the strip km: d/(2)wm+d) k2: k1k2 K: complete elliptical integral of first species l: Long
Concentric spheres	4π π ε ε 1R1− − 1R2{displaystyle {frac {4pi varepsilon}{{{{frac {1}{R_{1}}}}}{frac {1}{R_{2}}}}}}}}}}}}}}	ε: Allowance or dielectric constant
Two areas, of equal radius	2π π ε ε a␡ ␡ n=1∞ ∞ sinh (ln (D+D2− − 1))sinh (nln (D+D2− − 1))=2π π ε ε a[chuckles]1+12D+14D2+18D3+18D4+332D5+O(1D6)]=2π π ε ε a[chuckles]ln 2+γ γ − − 12ln (2D− − 2)+O(2D− − 2)]=2π π ε ε aD2− − 1log (q)[chuckles]END END q(1+iπ π log (q))− − iπ π − − END END q(1)]{cHFFFFFF}{cHFFFFFF}{cHFFFFFFFF}{cHFFFFFF}{cHFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFFFF}{cHFFFFFFFFFFFF}{cHFFFFFFFF}{cHFFFFFFFF}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF}{c}{cH00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cHFFFFFFFFFFFFFFFFFFFF00}{cHFFFFFFFFFFFFFFFFFFFF00}{cH00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cHFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{c}{cHFFFFFFFFFFFFFFFF	a: Radio d: Distance, d  2a D = d/2a, D ▪ 1 γ: constant of Euler q=D+D2− − 1{displaystyle q=D+{sqrt {D^{2}-1}}}}}} END END q(z)=▪ ▪ zInterpreter Interpreter q(z)Interpreter Interpreter q(z){displaystyle psi _{q}(z)={frac {partial _{z}Gamma _{q}(z)}{Gamma _{q}(z)}}}}}: the q-digamma function Interpreter Interpreter q(z){displaystyle Gamma _{q}(z)}: the q-Gamma function.
Sphere in front of a wall	4π π ε ε a␡ ␡ n=1∞ ∞ sinh (ln (D+D2− − 1))sinh (nln (D+D2− − 1)){displaystyle 4pi varepsilon asum _{n=1}^{infty }{frac {sinh left(ln left(D+{sqrt {D^{2}-1}}}{right)}{right)}{sinh left(nln left(D+{sqrt {w}{	a{displaystyle a}: Radio d{displaystyle d}: Distance, a}" xmlns="http://www.w3.org/1998/Math/MathML">d▪a{displaystyle d 2005}a}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5a63ce3b01161f8f4a757d6d8e0408dcdbe5b478" style="vertical-align: -0.338ex; width:5.544ex; height:2.176ex;"/> D=d/a{displaystyle D=d/a}
Sphere	4π π ε ε a{displaystyle 4pi varepsilon a}	a{displaystyle a}: Radio
Circular disk	8ε ε a{displaystyle 8varepsilon a}	a{displaystyle a}: Radio
Straight thin wire, finite length	2π π ε ε l l .... [chuckles]1+1.... (1− − ln 2)+1.... 2(1+(1− − ln 2)2− − π π 212)+O(1.... 3)]{displaystyle {frac {2pi varepsilon ell }{Lambda }left[1+{frac}{1}{Lambda }{left(1-ln 2right)}{frac {1}{1}{Lambda ^{2}}{1⁄2⁄2}{left(1⁄2}{1⁄2⁄2⁄2⁄2}}}}{1⁄2⁄2⁄2⁄2⁄2⁄2}}{1⁄2⁄2}}{1⁄2}}}}}	a{displaystyle a}: Wire radio l l {displaystyle ell }: Long .... =ln (l l /a){displaystyle Lambda =ln left(ell /aright)}

Capacitance measurement

Capacitance measurement is not only used to check the capacitance of a capacitor (component), but is also used, for example, in capacitive distance sensors to determine the distance. Other sensors (pressure, humidity, gases) often rely on a capacitance measurement.

According to the relationships mentioned above, the capacity can be determined as follows:

• Charge with constant current and observe voltage increase rate
• Measuring the resonant frequency of a LC resonant circuit formed with training
• Apply a AC voltage and measure current flow

In particular, the latter method is used in capacitance measuring devices, where not only the size of the current is recorded but also its phase relationship to the voltage. In this way, the impedance and loss angle or quality factor of the capacitor can also be determined.