Effective value

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Effective value (V)_RMS) of a sinusoidal wave

The root mean square value of an electrical quantity is called effective value. The concept of effective value is used especially to study periodic waveforms, despite being applicable to all waveforms, constant or not. It is sometimes referred to by the foreign term RMS (from English, root mean square).

Definition

The effective value of the intensity i(t) is the mean square value:

{displaystyle I_{rm {ef}}={sqrt {{1 over {T}}{int limits _{t_{0}}^{t_{0}+T}{i^{2}(t)},dt}}}}

where:

T

It's the signal period.

Similarly, the effective value of the voltage is:

{displaystyle V_{rm {ef}}={sqrt {{1 over {T}}{int limits _{t_{0}}^{t_{0}+T}{v^{2}(t)},dt}}}}

Physical meaning

The physical meaning of the effective value is to designate the value of a rigorously constant current that, when circulating on a certain ohmic resistance, would produce the same calorific effects as said variable current. In this way, a parallelism is established between any type of variable current and the direct current that simplifies the calculations with the latter.

Sometimes it is important to know the average power dissipated in an electrical resistor when the current is not constant. The average power dissipated is:

{displaystyle P_{rm {med}}={1 over {Delta }t}{int _{t_{0}}^{t_{0}+{Delta }t}{v(t) i(t)},dt}}

When said current is periodic, and taking into account Ohm's law:

{displaystyle P_{rm {med}}={1 over {T}}{int _{t_{0}}^{t_{0}+T}{R i^{2}(t)},dt}}

Which, by the definition of effective value, is the same as:

{displaystyle P_{rm {med}}=I_{rm {ef}}^{2} R}

RMS value for common waveforms

For periodic waveforms where there is a defined frequency, the effective value is independent of that frequency.

	Formula	Effective value
Continuous current, constant	${displaystyle y=A_{0},}$	$A_{0},$
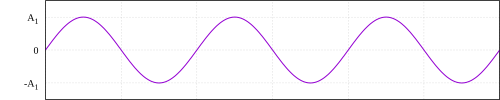
Sinusoidal wave	${displaystyle y=A_{1}sin(2pi ft),}$	${displaystyle {frac {A_{1}}{sqrt {2}}}}$
Modified sinusoidal wave	$<math alttext="{displaystyle y={begin{cases}0&operatorname {frac} (ft)<0.25\A_{1}&0.25<operatorname {frac} (ft)<0.5\0&0.5<operatorname {frac} (ft)0.75end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">and={0frac (ft).0.25A10.25.frac (ft).0.500.5.frac (ft).0.75− − A1frac (ft)▪0.75{displaystyle y={begin{cases}0 fakeoperatorname {frac} (ft){0.25A_{1}{1}{operatortorname {frac} (ft)}{5 fake0.5}{operatorname {frac}{ft}{.75-A_{1}{1⁄operatorname {frac}{<img alt="{displaystyle y={begin{cases}0&operatorname {frac} (ft)<0.25\A_{1}&0.25<operatorname {frac} (ft)<0.5\0&0.5<operatorname {frac} (ft)0.75end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/d16f59a57400dc035bc5d8425cda7efa44eca38c" style="vertical-align: -5.171ex; width:35.048ex; height:11.509ex;"/>$	${displaystyle {frac {A_{1}}{sqrt {2}}}}$
Square wave	$<math alttext="{displaystyle y={begin{cases}A_{1}&operatorname {frac} (ft)0.5end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">and={A1frac (ft).0.5− − A1frac (ft)▪0.5{displaystyle y={begin{cases}A_{1} strangeroperatorname {frac} (ft)≤5-A_{1} alienoperatorname {frac} (ft) offset0.5end{cases}}}}}}<img alt="{displaystyle y={begin{cases}A_{1}&operatorname {frac} (ft)0.5end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/b1147faa4b66211cbbc8a687d4231611e29b27a9" style="vertical-align: -2.505ex; width:27.493ex; height:6.176ex;"/>$	${displaystyle A_{1},}$
Square wave with continuous component	$<math alttext="{displaystyle y=A_{0}+{begin{cases}A_{1}&operatorname {frac} (ft)0.5end{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">and=A0+{A1frac (ft).0.5− − A1frac (ft)▪0.5{displaystyle y=A_{0}+{begin{cases}A_{1} dreamoperatorname {frac} (ft){0.5-A_{1}{1}{operatorname {frac} (ft) offset0.5end{cases}}}}}<img alt="{displaystyle y=A_{0}+{begin{cases}A_{1}&operatorname {frac} (ft)0.5end{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/219d36fb43253cd700ae68385b4c6ab2d40d5541" style="vertical-align: -2.505ex; width:33.13ex; height:6.176ex;"/>$	${displaystyle {sqrt {A_{0}^{2}+A_{1}^{2}}},}$
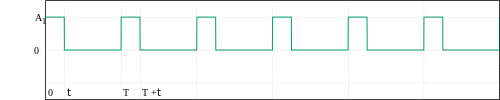
Pulse train	$<math alttext="{displaystyle y={begin{cases}A_{1}&operatorname {frac} (ft)Dend{cases}}}" xmlns="http://www.w3.org/1998/Math/MathML">and={A1frac (ft).D0frac (ft)▪D{displaystyle y={begin{cases}A_{1} strangeroperatorname {frac} (ft){D fakeoperatorname {frac} (ft) HCFCDend{cases}}}}}}}<img alt="{displaystyle y={begin{cases}A_{1}&operatorname {frac} (ft)Dend{cases}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/604fb9b622eb58a4555880ff8c156d71498e77d4" style="vertical-align: -2.505ex; width:24.637ex; height:6.176ex;"/>$	${displaystyle A_{1}{sqrt {D}}}$ See Note
triangular wave	${displaystyle y=left\|2A_{1}operatorname {frac} (ft)-A_{1}right\|}$	${displaystyle A_{1} over {sqrt {3}}}$
Wave in saw teeth	${displaystyle y=2A_{1}operatorname {frac} (ft)-A_{1},}$	${displaystyle A_{1} over {sqrt {3}}}$
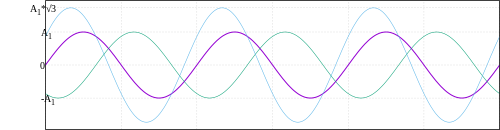
Phase to phase voltage	${displaystyle y=A_{1}sin(t)-A_{1}sin left(t-{frac {2pi }{3}}right),}$	${displaystyle A_{1}{sqrt {frac {3}{2}}}}$

Note: Where D, is expressed in "per unit" of the period T (D = t/T).

Wave Combinations

A fairly common case is a periodic wave that contains a DC component. In this case, the effective value is (indistinctly for voltage or current):

{displaystyle V_{rm {ef}}={sqrt {V_{rm {ef_{CC}}}^{2}+V_{rm {ef_{CA}}}^{2}}}}

where ${displaystyle V_{rm {ef_{CC}}}}$ is the effective value of the continuous component and ${displaystyle V_{rm {ef_{CA}}}}$ is the effective value of the alternating component.

Generalizing, the effective value of a combination of waves, if they are orthogonal to each other, is:

{displaystyle V_{rm {ef_{Total}}}={sqrt {V_{rm {ef_{1}}}^{2}+V_{rm {ef_{2}}}^{2}+dots +V_{rm {ef_{n}}}^{2}}}}

Más resultados...