Doppler effect

ImprimirCitar

Change of the wavelength caused by the transmitter's movement.

Doppler effect of sound flow around a car.

Claxon of a passing car

The Doppler effect, (named after the Austrian physicist and mathematician Christian Andreas Doppler) is the change in the apparent frequency of a wave produced by the relative motion of the source with respect to its observer.

There are everyday examples of the Doppler effect in which the speed at which the object emitting the waves moves is comparable to the speed of propagation of those waves. The speed of an ambulance (50 km/h) may seem insignificant compared to the speed of sound at sea level (about 1,235 km/h), however it is about 4% of the speed of sound, a fraction enough large enough to cause the change in the sound of the siren from a higher pitch to a lower pitch to be clearly appreciated, just at the moment the vehicle passes the observer.

In the case of the visible spectrum of electromagnetic radiation, if the object moves away, its light shifts to longer wavelengths, producing a redshift. If the object gets closer, its light has a shorter wavelength, shifting towards blue. This shift towards red or blue is very slight even for high velocities, such as the relative velocities between stars or between galaxies, and cannot be captured by the human eye, only measured indirectly using precision instruments such as spectrometers. If the emitting object moved at significant fractions of the speed of light, the variation in wavelength would be directly appreciable.

Discovery

Doppler proposed this effect in 1842 in his treatise Über das farbige Licht der Doppelsterne und einige andere Gestirne des Himmels (On the color of light in binary stars and other bodies). The Dutch scientist Christoph Hendrik Diederik Buys Ballot investigated this hypothesis in 1845 for the case of sound waves and confirmed that the pitch of a sound emitted by a source approaching the observer is higher pitched than if the source is moving away. Hippolyte Fizeau independently discovered the same phenomenon in the case of electromagnetic waves in 1848. In France this effect is known as the "Doppler-Fizeau effect" and in the Netherlands as the "Doppler-Gestirne effect". In Great Britain, John Scott Russell made an experimental study of the Doppler effect (1848).

General information

In classical physics, where the velocities of the emitter (also called "source") and the receiver (or also "observer") regarding the medium are less than the speed of the waves in the medium itself, the relation between the observed frequency $f$ and frequency emitted ${displaystyle f_{text{0}}}$ is given by:

${displaystyle f=left({frac {v+v_{r}}{v+v_{s}}}right)f_{0}}$
Symbol	Name
$f$	Frequency observed
$f_{0}$	Frequency emitted
$v$	Speed of waves in the middle
${displaystyle v_{r}}$	Speed of the receiver in relation to the medium; positive if the receiver is moving towards the emitter (and negative in the opposite sense)
${displaystyle v_{s}}$	Speed of the source with respect to the medium; positive if the source is removed from the receiver (and negative in the opposite sense)

(Conclusion: the frequency increases when source and observer get closer to each other, and decreases when they move away).

In the above formula it is assumed that the source is approaching (or moving away) "directly" from the observer. If the source approaches the observer with constant velocity, but on a "non-incident" path (such as an aircraft in flight relative to an observer on the ground), then:

The frequency the observer hears first is higher than the frequency emitted from the object.
Below is a gradual decrease in the perceived frequency as the source approaches the observer, coinciding with the perceived frequency with the original when the wave arrives from a perpendicular direction to the relative movement (i.e. when it was issued from the closest point to the observer, although when the wave, the source and the observer are no longer in their nearest position).
Finally, the observer will perceive a continuing decrease in frequency as the source is removed.

When the observer is very close to the trajectory of the object, the transition from high to low frequency is very abrupt. Instead, when the observer is far from the object's trajectory, the transition from high to low frequency is gradual.

If the speeds ${displaystyle v_{text{s}},}$ and ${displaystyle v_{text{r}},}$ are small compared to wave speed, the ratio of observed frequency $f$ and frequency emitted ${displaystyle f_{text{0}}}$ is approximately

Frequency observed	Frequency change
${displaystyle f=left(1+{frac {Delta v}{v}}right)f_{0}}$	${displaystyle Delta f={frac {Delta v}{v}}f_{0}}$

where

{displaystyle Delta f=f-f_{0},}

{displaystyle Delta v=v_{text{r}}-v_{text{s}},}

is the speed of the receiver regarding the source: it is positive when the source and the receiver approach.

(Demonstration:)

Dada ${displaystyle f=left({frac {v+v_{text{r}}}{v+v_{text{s}}}}right)f_{0},}$

dividing by $v$

${displaystyle f=left({frac {1+{frac {v_{text{r}}}{v}}}{1+{frac {v_{text{s}}}{v}}}}right)f_{0}=left(1+{frac {v_{text{r}}}{v}}right)left({frac {1}{1+{frac {v_{text{s}}}{v}}}}right)f_{0},}$

From ${displaystyle {frac {v_{text{s}}}{v}}ll 1}$ geometric expression can be deduced:

${displaystyle {frac {1}{1+{frac {v_{text{s}}}{v}}}}approx 1-{frac {v_{text{s}}}{ver}}}$

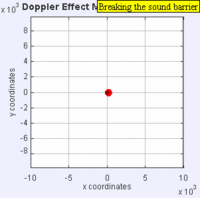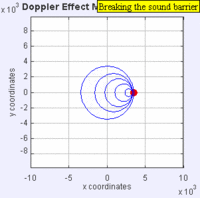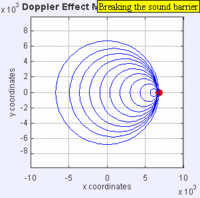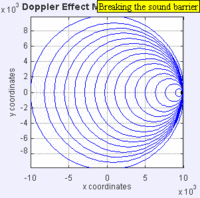
Stationary, subsonic, sonic and supersonic situation.

The following four graphs include an animation with the analysis of the behavior of sound waves in the four characteristic cases of the Doppler effect in relation to the speed of the emitter with respect to the speed of sound propagation in air (Mach 1):

A fixed audio source produces sound waves at a constant frequency

f

, and waveheads spread symmetrically away from the source at a constant speed c. The distance between the waveheads is the wavelength. All observers will hear the same frequency, which will be equal to the actual frequency of the source where

f = f 0

The same sound source is radiating sound waves at a constant frequency in the same medium. However, now the sound source moves with a speed of

♫ s = 0.7 c

(Mach 0.7). Since the source is moving, the center of each new wave front is slightly moved to the right. As a result, waveheads begin to accumulated on the right side (before) and are further distanced on the left side (behind) of the source. An observer in front of the source will hear a higher frequency:

$f = c + 0 / c - 0.7 c f 0 = 3.33 f 0$ and an observer behind the source will hear a lower frequency: $f = c - 0 / c + 0.7 c f 0 = 0.59 f 0$ .

Now the source is moving at the sound speed in the middle (

♫ s = c

(i.e. Mach 1). The wave fronts in front of the source are now all accumulated at the same point. As a result, an observer in front of the source will not detect anything until the source reaches its position

$f = c + 0 / c - c f 0 = \infty$ and an observer behind the source will hear a lower frequency $f = c - 0 / c + c f 0 = 0.5 f 0$ .

The sound source has already exceeded the sound speed in the middle, and moves to 1.4 c (Mach 1.4). Since the source is moving faster than the sound waves it creates, what it really does is direct the wave front as it advances. The sound source will pass before an observer at rest before the observer hears the sound. As a result, an observer in front of the source will perceive:

$f = c + 0 / c - 1.4 c f 0 = -2.5 f 0$ and an observer behind the source will hear a lower frequency: $f = c - 0 / c + 1.4 c f 0 = 0.42 f 0$ .

Analysis

To understand what happens, consider the following analogy. Someone throws a ball every second at a man. The balls are assumed to travel with constant velocity. If the pitcher is stationary, the man is going to receive a ball every second. However, if the pitcher is moving towards the man, he is going to catch the balls more frequently because the balls will be less spaced. The reverse is true if the pitcher moves away from the man. So it is actually the wavelength that is affected; as a consequence, the received frequency is also affected. It can also be stated that the speed of the wave remains constant, while changes in the wavelength occur; and therefore the frequency changes as well.

For a resting observer over the medium, if a moving source is emitting waves with a given actual frequency ${displaystyle f_{text{0}}}$ (in this case, the wavelength changes but the wave transmission speed remains constant, so the transmission speed of the wave does not depend on the speed of source) then the observer detects waves at a frequency $f$ given by:

{displaystyle f=left({frac {c}{c+v_{text{s}}}}right)f_{0}}

A similar analysis for a moving observer and a stationary source (in this case, the wavelength remains constant, but due to motion, the speed at which the observer receives the waves, and therefore the speed of transmission of the wave [with respect to the observer] changes) produces the observed frequency:

{displaystyle f=left({frac {c+v_{text{r}}}{c}}right)f_{0}}

This can be generalized into the equation presented in the previous section:

{displaystyle f=left({frac {c+v_{text{r}}}{c+v_{text{s}}}}right)f_{0}}

An interesting effect was predicted by Lord Rayleigh in his classic book on sound: if the source approaches the observer at twice the speed of sound, a piece of music emitted by that source would be heard at the correct time and pitch, but inversely (that is, the notes at the end of the piece would reach the observer before those at the beginning). The Doppler effect on sound is only clearly perceived with objects moving at a high speed: the change in musical pitch frequency implies a speed of around 40 meters per second (144 km/h). However, changes in amplitude of sounds from moving emitters can easily be mistaken for small changes in frequency. Neil A Downie has shown how the Doppler effect can be made much more easily audible by using an ultrasonic emitter (eg 40 kHz) emitting from moving objects. The observer must use a heterodyne frequency converter (such as those used in many bat detectors) capable of working in the band up to 40 kHz. In this case, with the receiver set to translate the waves received into the 2000 Hz band to make them audible, it is enough for the transmitter to move at just 2 meters per second for the observer to perceive a frequency shift of one whole tone (240 Hz).

Non-invention transmitter in the receiver

In the case of a moving emergency vehicle siren passing close to an observer, it will begin to sound at a higher frequency than its stationary tone. It will decrease as it gets closer, and will continue to decrease (below its stationary pitch) as it moves away from the observer. Astronomer John Dobson explained the effect this way:

"The reason you perceive how gradually slides Mermaid's tone is because Don't kneel the observer. "

In other words, if the siren were to approach the observer directly (with constant velocity), the perceived frequency would remain unchanged until the vehicle caught up with it, only to immediately jump to a new lower pitch as soon as it started to move away. Because the vehicle does not pass through the exact point occupied by the observer, but rather passes it at a certain distance, its relative velocity presents a radial component that does not remain constant, but rather varies as a function of the angle between its line of sight and the speed of the vehicle carrying the siren:

{displaystyle v_{text{radial}}=v_{text{s}}cdot cos {theta }}

where $theta$ is the angle between the speed of progress of the object and the line of vision from the object to the observer.

Algebra of the Doppler effect in sound waves

Observer approaching a source

Let's imagine an observer O moves with a speed ${displaystyle v_{o},}$ that has a direction and sense to a sound source S which is at rest. The medium is air and is also at rest. The source emits a speed sound ${displaystyle v,}$ frequency $f,$ and wavelength ${displaystyle lambda ,}$ . Therefore, the speed of the waves regarding the observer will not be ${displaystyle v,}$ but the following:

{displaystyle v'=v+v_{o}}

However, since the speed of the medium does not change, the wavelength will be the same, therefore, if:

{displaystyle v=fcdot lambda Rightarrow f={frac {v}{lambda }}}

But as we mentioned in the first explanation, the observer when approaching the source will hear a sharper sound, this implies that his frequency is greater. This greater frequency captured by the observer is called the apparent frequency, which we call it ${displaystyle f',}$ .

{displaystyle f'={frac {v'}{lambda }}={frac {v+v_{o}}{lambda }}={frac {v}{lambda }}+{frac {v_{o}}{lambda }}=f+{frac {v_{o}}{lambda }}=fcdot {bigg (}1+{frac {v_{o}}{fcdot lambda }}{bigg)}=fcdot {bigg (}1+{frac {v_{o}}{v}}{bigg)}}

The observer will hear a sound of greater frequency because ${displaystyle textstyle left(1+{tfrac {v_{o}}{v}}right)geq 1}$

Observer moving away from a source

Let us analyze the opposite case: when the observer moves away from the source, the speed will be ${displaystyle v'=v-v_{o},}$ and similarly we can deduce that ${displaystyle textstyle f'=fcdot left(1-{tfrac {v_{o}}{v}}right)}$

Source approaching the observer

In this case, the apparent frequency perceived by the observer will be higher than the real frequency emitted by the source, which causes the observer to perceive a higher pitched sound.

Therefore, the perceived wavelength for a moving source with a speed ${displaystyle v_{s},}$ It will be:

{displaystyle {mathcal {lambda }}'=lambda -Delta lambda }

Like ${displaystyle lambda ={frac {v}{f}}}$ we can deduce that:

{displaystyle f'={frac {v}{lambda '}}={frac {v}{lambda -{frac {v_{s}}{f}}}}={frac {v}{{frac {v}{f}}-{frac {v_{s}}{f}}}}=fcdot {bigg (}{frac {v}{v-v_{s}}}{bigg)}}

Source moving away from the observer

Making a similar reasoning for the opposite case: source moving away; We can conclude that the frequency perceived by an observer at rest with a moving source will be:

{displaystyle f'=fcdot {Bigg (}{frac {1}{1pm {frac {v_{s}}{v}}}}{Bigg)}}

When the source approaches the observer, a sign (-) will be placed in the denominator, and when the source moves away it will be replaced by (+).

After reading the above, the following question arises: What will happen if the source and the observer move at the same time? In this particular case, the following formula is applied, which is nothing more than a combination of the two:

{displaystyle f'=fcdot {bigg (}{frac {vpm v_{o}}{vmp v_{s}}}{bigg)}}

The sense of displacement of the source and the observer are inverse:

If the observer approaches the source the numerator is positive, if it moves away it is negative.

If the sound source approaches the observer the denominator is negative, if it moves away it is positive.

It can be the case that the numerator and denominator are a sum, and also that the numerator and denominator are a subtraction.

Example

An observer moves at a speed of 42 m/s towards a resting trompetist. The trumpetist is playing (emitting) the note the (440 Hz). What frequency will the observer perceive, knowing that ${displaystyle v_{rm {sonido}},}$ = 340 m/s

Solution: If the observer approaches the source, it implies that the speed with which he will perceive each wave front will be greater, therefore the apparent frequency will be greater than the real one (at rest). For this to happen we must apply the sign (+) in the equation.

{displaystyle f'=fcdot {bigg (}1pm {frac {v_{o}}{v}}{bigg)}}

{displaystyle f'=440mathrm {Hz} cdot {bigg (}1+{frac {42mathrm {m/s} }{340mathrm {m/s} }}{bigg)}rightarrow f'=494,353mathrm {Hz} }

In this particular case, the trumpeter emits the note la at 440 Hz; however, the observer perceives a note that vibrates at a frequency of 494.353 Hz, which closely approximates the frequency belonging to the note si. Musically speaking, the observer perceives the sound with a higher pitch than it is actually emitted.

Algebra of the Doppler effect in electromagnetic waves

In the case of electromagnetic waves the doppler effect formula is: ${displaystyle f'=gamma {frac {c+v}{c}}f}$ Being f the frequency of the transmitter, f' the one that sees the receiver, v the speed of the transmitter regarding the receiver and $gamma$ the Lorentz factor given by:

{displaystyle gamma ={frac {1}{sqrt {1-{cfrac {v^{2}}{c^{2}}}}}}}

(Demonstration:)

To analyze the case of electromagnetic waves we will use the transformations of Lorentz to move from the transmitter reference system to the receiver; we will denote the primate quantities of the receiver and the non-primary ones of the transmitter. We will assume that the wave and the transmitter moves to the right.

Suppose the emitter is emitting a wave of the form:

{displaystyle Phi (x,t)=Phi (omega t-kx)}

The coordinate transformations will be:

{displaystyle x=gamma (x'-vt')}

{displaystyle t=gamma (t'-{frac {vx'}{c^{2}}})}

Substituting in the wave function and comparing to the wave function in the receiving reference system:

{displaystyle Phi (x,t)=Phi (omega t-kx)=Phi (gamma (omega +kv)t'-gamma ({frac {vomega }{c^{2}}}+k)x')=Phi '(omega 't'-k'x')}

We get:

{displaystyle omega '=gamma (omega +kv)=gamma {frac {c+v}{c}}omega }

Or in terms of frequencies:

{displaystyle f'=gamma {frac {c+v}{c}}f}

Applications

Astronomy

Red correction of spectral lines in the optical spectrum of a super cluster of distant galaxies (right), compared to that of the Sun (left)

The Doppler effect on electromagnetic waves such as light is very useful in astronomy, and it manifests itself in the so-called redshift or blueshift. It has been used to measure the speed at which stars and galaxies are moving towards or away from Earth; that is, their radial velocities. This physical phenomenon is used to detect binary stars, to measure the speed of rotation of stars and galaxies, or to detect exoplanets. (Note that redshift is also used to measure the expansion of space, although in this case it is not really a Doppler effect.)

The use of the Doppler effect on light in astronomy depends on the knowledge that the spectra of stars are not homogeneous. They exhibit definite absorption lines of frequencies that correspond to the energies required to excite the electrons of various elements from one level to another. The Doppler effect is recognizable in the fact that the known patterns of absorption lines do not always appear to coincide with the frequencies obtained from the spectrum of a stationary light source. Because blue light has a higher frequency than red light, the spectral lines of an approaching astronomical light source exhibit a blueshift, and those of a receding one exhibit a redshift.

Among the closest stars to Earth, the fastest radial velocities with respect to the Sun are +308 km/s (BD-15°4041, also known as LHS 52, located 81.7 light-years away) and –260 km/s (Woolley 9722, also known as Wolf 1106 and LHS 64, located 78.2 light-years away). A positive radial velocity means that the star is moving away from the Sun, negative that it is getting closer.

Radar

Main article: Radar doppler

The Doppler effect is used in some types of radar to measure the speed of detected objects. A radar beam is fired at a moving target (for example, a car, as in police use of radar to detect the speed of vehicles) as it approaches or recedes from the radar source. Each successive radar wave has to travel further to reach the car, before being reflected and detected again near the source. As each wave has to move further, the distance between each wave increases, producing an increase in wavelength. In some situations, the radar beam is used while the car is moving, and if it approaches the observed vehicle, then each successive wave travels a shorter distance, producing a decrease in wavelength. In any of these situations, calculations of the Doppler effect allow the speed of the vehicle observed by the radar to be accurately determined. On the other hand, the proximity fuze, developed during World War II, relies on Doppler radar to detonate explosives at the right time based on their height above ground or their distance from the target.

Because doppler displacement affects the incident wave in the target, as well as the wave reflected back on the radar, the change in the frequency observed by a moving radar over a target also in motion is a function of its relative speed. ${displaystyle Delta v}$ , and it is double that would be recorded directly between the transmitter and the receiver:

{displaystyle Delta f={frac {2Delta v}{c}}f_{0}}

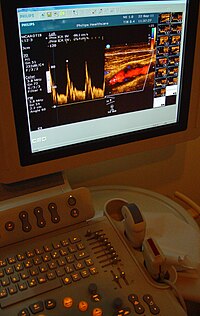
Medical Imaging and Blood Flow Measurement

Main article: Ultrasound#Ecography doppler

Doppler ultrasound in blood flow color in a carotid artery - scanner and screen

An echocardiogram can, within limits, produce an accurate assessment of the direction of blood flow and the velocity of blood and cardiac tissue at any arbitrary point using the Doppler effect. One of the limitations is that the ultrasound beam must be as parallel as possible to the direction of blood flow. Velocity measurements allow assessment of heart valve areas and their function; of all possible abnormal communications between the left and right side of the heart; from any blood leaking through the valves (valvular regurgitation); and the calculation of cardiac output.

Although the term "doppler" has become a byword for "speed measurement" In medical imaging, in many cases, it is not the frequency shift (Doppler shift) of the received signal that is measured, but the phase shift (i.e. when the received signal arrives, which allows calculating distances).

Measurements of blood flow velocity are also used in other fields of ultrasound medicine, such as obstetrics and neurology. Measurement of the velocity of blood flow in arteries and veins based on the Doppler effect is an effective tool for the diagnosis of vascular problems such as stenosis.

Flow velocity measurement

Instruments such as the laser doppler velocimeter (LDV) and the acoustic doppler velocimeter (ADV) have been developed to measure velocities in fluid flow. The LDV emits a beam of light and the ADV emits a train of ultrasonic acoustic waves, and measuring the Doppler effect at the wavelengths of the reflections of the particles that move with the flow of the fluid. The actual flow is calculated as a function of the velocity of the liquid and the solid phase. This technique allows non-invasive flow measurements to be made, with high precision and with high frequency.

Velocity profile measurement

Originally developed for velocity measurements in medical applications (blood flow), Doppler Ultrasonic Velocimetry (UDV) allows near real-time measurement of the complete velocity profile in almost any fluid containing suspended particles, such as dust, gas bubbles, or emulsions. Flows can be pulsating, oscillating, laminar or turbulent, stationary or transitory. This technique is completely non-invasive.

Satellite Communications

Satellites move very quickly and can have a Doppler shift of tens of kilohertz from a ground station. The speed of the satellites, on which the magnitude of the Doppler effect depends, undergoes changes due to the curvature of the Earth. To avoid this problem, dynamic Doppler compensation has been devised, whereby the frequency of the signal is changed several times during transmission, so that the satellite receives a constant frequency signal.

Audio

The Leslie speaker, commonly associated with popular Hammond organs, utilizes the Doppler effect by using an electric motor to rotate an acoustic horn around a speaker, rotating the orientation 360° of sound with each turn. This translates to the human ear in that the frequencies fluctuate rapidly for each note on the keyboard.

Vibration measurement

A laser doppler vibrometer (LDV) is a method by which vibration measurement can be obtained without the need for contact. The laser beam is directed at the surface to be examined from the LDV, and the amplitude of the vibration and its frequency are extracted from the Doppler shift of the frequency of the laser beam due to the movement of the surface.

Developmental Biology

During the cleavage of vertebrate embryos, the process of gene expression produces a series of sweeping waves through the presomitic mesoderm, the tissue from which vertebrate precursors (somites) are formed. A new somite is formed by the arrival of a wave at the anterior end of the presomitic mesoderm. In zebrafish, it has been shown that the shortening of the presomitic mesoderm during segmentation produces a Doppler effect that guides the movements of the anterior end tissue through waves. This Doppler effect contributes to the control of the segmentation period.

Inverse Doppler Effect

Since 1968, scientists such as Victor Veselago have speculated about the possibility of a reverse Doppler effect. The experiment that he claimed to have detected this effect was carried out by Nigel Seddon and Trevor Bearpark in Bristol, UK in 2003.

Researchers at many universities such as Swinburne University of Technology and the University of Shanghai for Science and Technology showed that this effect can also be observed at optical frequencies. This was possible thanks to the generation of a photonic crystal on which they projected a laser beam. This made the crystal behave like a superprism, and the inverse Doppler effect could be observed.

Contenido relacionado

Más resultados...