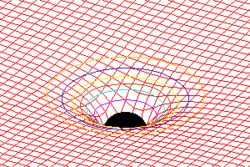
Differential equation

ImprimirCitar

Heat transfer visualization in a pump chamber, created by solving the heat equation. The heat is generated internally in the chamber and cooled on the edges, giving a stationary state of temperature distribution.

A differential equation is a mathematical equation that relates a function to its derivatives. In applied mathematics, functions usually represent physical quantities, derivatives represent their rates of change, and the equation defines the relationship between them. Because these relationships are so common, differential equations play a central role in many disciplines, including engineering, physics, chemistry, economics, and biology.

In applications of mathematics, problems often arise in which the dependence of one parameter on another is unknown, but it is possible to write an expression for the rate of change of one parameter relative to another (derivative). In this case, the problem is reduced to finding a function by its derivative related to some other expressions.

In pure mathematics, differential equations are studied from different perspectives, most concerning the set of solutions of the functions that satisfy the equation. Only the simplest differential equations can be solved by explicit formulas; however, some properties of the solutions of a certain differential equation can be determined without finding its exact form.

If the exact solution cannot be found, it can be obtained numerically, by approximation using computers. Dynamical systems theory emphasizes the qualitative analysis of systems described by differential equations, while many numerical methods have been developed to determine solutions with some degree of accuracy.

History

Main article: History of differential equations

Cover of the Method of Fluxons and Infinite Series, a work that was published in 1736, even though Newton had finished it in 1671.

Differential equations first appeared in the calculus works of Newton and Leibniz. In 1671, in Chapter 2 of his work Method of Fluxions and Infinite Series, Isaac Newton listed three classes of differential equations:

{displaystyle {frac {dy}{dx}}=f(x)}

{displaystyle {frac {dy}{dx}}=f(x,y)}

{displaystyle x_{1}{frac {partial y}{partial x_{1}}}+x_{2}{frac {partial y}{partial x_{2}}}=y}

He solved these equations and others using infinite series and discussed the non-uniqueness of the solutions.

Jakob Bernoulli proposed Bernoulli's differential equation in 1695. This is an ordinary differential equation of the form

{displaystyle y'+P(x)y=Q(x)y^{n},}

for which, in the following years, Leibniz obtained his solutions through simplifications.

Stationary waves on a vibrant rope. The fundamental mode and the first five overtones of the harmonic series are observed.

Historically, the problem of a vibrating string, such as that of a musical instrument, was studied by Jean le Rond d'Alembert, Leonhard Euler, Daniel Bernoulli, and Joseph-Louis Lagrange. In 1746, d'Alembert discovered the one-dimensional wave equation, and within ten years Euler discovered the three-dimensional wave equation.

The Euler-Lagrange equations were developed in the 1750s by Euler and Lagrange in connection with their studies of the tautochrone problem. This is the problem of determining a curve in which a weighted particle will fall on a fixed point in a certain fixed amount of time, independent of the starting point.

Lagrange solved this problem in 1755 and sent the solution to Euler. Both developed Lagrange's method and applied it to mechanics, which led to Lagrangian mechanics.

In 1822 Fourier published his work on heat transfer in Théorie analytique de la chaleur (Analytic Theory of Heat), in which he based his reasoning on Newton's law of cooling, that is, that the heat transfer between two adjacent molecules is proportional to extremely small differences in their temperatures. In this book Fourier exposes the heat equation for the conductive diffusion of heat. This equation in partial derivatives is currently the object of study in mathematical physics.

Stochastic differential equations, which extend both the theory of differential equations and the theory of probability, were introduced with rigorous treatment by Kiyoshi Itō and Ruslan Stratonovich during the 1940s and 1950s.

Types

Differential equations can be divided into several types. Apart from describing the properties of the equation itself, the classes of differential equations can help in finding the choice of approximation to a solution. It is very common for these distinctions to include whether the equation is: ordinary/in partial derivatives, linear/nonlinear, and homogeneous/inhomogeneous. This list is too big; there are many other properties and subclasses of differential equations which can be very useful in specific contexts.

Ordinary Differential Equations

Main article: Ordinary differential equation

The trajectory of a projectile launched from a cannon follows a curve defined by an ordinary differential equation that is obtained from the second law of Newton.

An ordinary differential equation (ODE) is an equation that contains a function of an independent variable and its derivatives. The term ordinary is used in contrast to the partial differential equation, which can be with respect to more than one independent variable.

Linear differential equations, which have solutions that can be added and multiplied by coefficients, are well defined and understood, and have exact solutions that can be found. In contrast, the ODEs whose solutions cannot be added are non-linear, and their solution is more intricate, and very rarely can be found in the exact form of elementary functions: the solutions are usually obtained in the form of series or integral form. Numerical and graphical methods for ODEs can be performed manually or by computers, the solutions of the ODEs can be approximated and their result can be very useful, often enough to dispense with the exact and analytical solution.

Equation in partial derivatives

Main article: Equation in partial derivatives

Variation of the temperature profile solution of the heat equation in a two-dimensional problem.

A partial differential equation (PDE) is a differential equation that contains a multivariable function and its partial derivatives. These equations are used to formulate problems involving functions of several variables, and can be solved manually, to create a computer simulation.

PDEs can be used to describe a wide variety of phenomena such as sound, heat, electrostatics, electrodynamics, fluid dynamics, elasticity, or quantum mechanics. These different physical phenomena can be formalized in terms of PDEs. With ordinary differential equations it is very common to make one-dimensional models of dynamic systems, and partial differential equations can be used to model multidimensional systems. PDEs have a generalization to stochastic partial differential equations.

Linear Differential Equations

Main article: Linear differential equation

A differential equation is linear when its solutions can be obtained from linear combinations of other solutions. If it is linear, the differential equation has its derivatives with a maximum power of 1 and there are no terms where there are products between the unknown function and/or its derivatives. The characteristic property of linear equations is that their solutions have the form of an affine subspace of a space of appropriate solutions, the result of which is developed in the theory of linear differential equations.

Homogeneous linear differential equations are a subclass of linear differential equations for which the solution space is a linear subspace, that is, the sum of any set of solutions or multiples of solutions, is also a solution. The coefficients of the unknown function, and its derivatives in a linear differential equation can be functions of the variable or independent variables, if these coefficients are constant, then we speak of linear differential equations with constant coefficients.

An equation is said to be linear if it has the form:

${displaystyle ,a_{n}(x)y^{(n)}+a_{n-1}(x)y^{(n-1)}+dots +a_{1}(x)y'+a_{0}(x)y=g(x)}$

That is:

Neither function nor its derivatives are elevated to any power other than one or zero.
In each coefficient that appears multiplying only the independent variable.
A linear combination of your solutions is also a solution to the equation.

Examples:

${displaystyle ,y'-y=0}$ is an ordinary linear differential equation of first order, has as solutions ${displaystyle y=f(x)=kcdot e^{x}}$ , with k any real number.
${displaystyle ,y''+y=0}$ is an ordinary linear differential equation of second order, has as solutions ${displaystyle y=f(x)=acos(x)+bsin(x),}$ , with a and b real.
${displaystyle ,y''-y=0}$ is an ordinary linear differential equation of second order, has as solutions ${displaystyle ,acdot e^{x}+bcdot 1/(e^{x})}$ , with a and b real.

Nonlinear Differential Equations

Very few methods exist for solving nonlinear differential equations exactly; those that are known it is very common that they depend on the equation having particular symmetries. Nonlinear differential equations can exhibit very complicated behavior in large intervals of time, characteristic of chaos. Each of the fundamental questions of the existence, uniqueness, and extensibility of solutions for nonlinear differential equations, and the well-defined problem of initial and boundary condition problems for nonlinear PDEs are difficult problems and their resolution in special cases. it is considered to be a significant advance in mathematical theory (eg the existence and smoothness of Navier-Stokes). However, if the differential equation is a correctly formulated representation of a significant physical process, then a solution is expected.

Nonlinear differential equations usually appear by means of approximations to linear equations. These approximations are valid only under restricted conditions. For example, the harmonic oscillator equation is an approximation of the nonlinear equation of a pendulum that is valid for small oscillation amplitudes (see below).

Semilinear and Quasilinear Equations

There is no general procedure for solving nonlinear differential equations. However, some particular cases of nonlinearity can be solved. Of interest are the semilinear case and the quasilinear case.

An ordinary differential equation of order n it is called quasilineal if it is "linear" in the derivative of order n. More specifically, if the ordinary differential equation for function ${displaystyle scriptstyle y(x)}$ can be written in the form:

${displaystyle f(y^{(n)},y^{(n-1)},dotsy'',y',y,x)=0,qquad qquad f_{1}(z):=f(z,alpha _{n-1},dotsalpha _{2},alpha _{1},alpha _{0},beta _{0})}$

It is said that this equation is quasi-linear if ${displaystyle scriptstyle f_{1}(cdot)}$ It's an aphin function, that is, ${displaystyle scriptstyle f_{1}(z)=az+b}$ .

An ordinary differential equation of order n is called semilineal if it can be written as a sum of a "linear" function of the derivative of order n plus any function of the rest of derivatives. Formally, if the ordinary differential equation for function ${displaystyle scriptstyle y(x)}$ can be written in the form:

${displaystyle f(y^{(n)},y^{(n-1)},dotsy'',y',y,x)={hat {f}}(y^{(n)},x)+g(y^{(n-1)},dotsy',y,x)qquad qquad f_{2}(z):={hat {f}}(z,beta _{0})}$

This equation is said to be semi-linear if ${displaystyle scriptstyle f_{2}(cdot)}$ It's a linear function.

Equation Order

Differential equations are described by their order, determined by the term with derivatives of highest order. An equation containing only simple derivatives is a first-order differential equation, an equation containing up to second derivatives is a second-order differential equation, and so on.

Examples of order in equations:

First-order differential equation: ${displaystyle y'+y(x)=f(x)}$
Second-order differential equation: ${displaystyle y''+4y=0}$
Third-order differential equation: ${displaystyle xy'''-2xy''+4y'=0}$
Second variable coefficient equation:

${displaystyle y''+2xy'+4y=0}$

Equation Degree

It is the power of the highest order derivative that appears in the equation, as long as the equation is in polynomial form, otherwise it is considered to have no degree.

Exact Differential Equations

Throughout this section, you will find differential equations written as: ${displaystyle P(x,y)dx+Q(x,y)dy=0}$ and ${displaystyle y'=-{P(x,y) over Q(x,y)}}$ without applying any distinction between the first and second equation.

It will be assumed that P and Q are defined functions in an open rectangle $R$ in $mathbb{R} ^{2}$ don't null at once.

It is said that the equation is accurate if there is an R function $rightarrow$ $R$ derivable such that ${displaystyle F_{x}(x,y)=P(x,y)}$ and ${displaystyle F_{y}(x,y)=Q(x,y)}$ ${displaystyle forall (x,y)in R}$

The importance of accuracy is that ${displaystyle F(x,y)=c}$ is a family of integral curves deducting implicitly from x: ${displaystyle F_{x}+F_{y}y'=0}$ So, ${displaystyle F(x,y)=c}$ sat ${displaystyle y'=-{P(x,y) over Q(x,y)}}$ .

A criterion that can be used to know exactly when an equation is accurate is based on the fact that P and Q are continuous functions and have partial continuous derivatives in R. If the equation ${displaystyle P(x,y)dx+Q(x,y)dy=0}$ It's exact differential, then, it's proven that ${displaystyle P_{y}=Q_{x}}$ in R.

Assuming that ${displaystyle P_{y}=Q_{x}}$ in R and we searched F such that ${displaystyle F_{x}=}$ P ${displaystyle F_{y}=Q}$ . Integrating the equation ${displaystyle F_{x}=}$ P regarding x: ${displaystyle F(x,y)=int P(x,y)dx+C(y)}$ where C(y) is the constant integration dependent on and.

Setting the condition ${displaystyle F_{y}=Q}$ is obtained: ${displaystyle C'(y)=Q(x,y)-{partial over partial y}int P(x,y)dx}$ where, applying ${displaystyle P_{y}=Q_{x}}$ , the right side of equality is a function of the variable and independent of x.

Finally:

${displaystyle F(x,y)=int P(x,y)dx+int (Q(x,y)-{partial over partial y}int P(x,y)dx)dy}$

In this way a method has been obtained after calculating the integral curves of an accurate differential equation ${displaystyle F(x,y)=c}$ showing the theorem stated above.

Examples

In the first set of examples, let u be an unknown function that depends on x, and c and ω are known constants. Note that both ordinary and partial differential equations can be classified as linear and nonlinear.

Regular linear differential equation to constant coefficients of first order:

{displaystyle {frac {du}{dx}}=cu+x^{2}.}

Second order standard linear differential equation:

{displaystyle {frac {d^{2}u}{dx^{2}}}-x{frac {du}{dx}}+u=0.}

La masa colgada del resorte forma un oscilador armónico, una ecuación diferencial permite expresar las relaciones que debe obedecer el movimiento de la masa.

A solution is given by ${displaystyle y=f(x)=AX}$

Ordinary linear differential equation to second order homogeneous constant coefficients describing a harmonic oscillator:

{displaystyle {frac {d^{2}u}{dx^{2}}}+omega ^{2}u=0.}

Normal nonlinear inhomogeneous differential equation of first order:

{displaystyle {frac {du}{dx}}=u^{2}+4.}

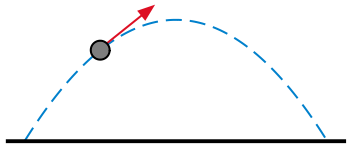
Nonlinear ordinary differential equation (due to the second order function), which describes the movement of a pendulum of length L:

{displaystyle L{frac {d^{2}u}{dx^{2}}}+gsin u=0.}

In the following set of examples, the unknown function u depends on two variables x and t or x e y.

First-order homogeneous linear partial derivative equation, then:

{displaystyle {frac {partial u}{partial t}}+t{frac {partial u}{partial x}}=0.}

Laplace equation on a crown (r=2 and R=4) with Dirichlet contour conditions: u(r=2)=0 and u(r=4)=4sin(5*θ).

Equation in linear partial derivatives homogenous to constant coefficients of second order of the elliptical type, the equation of Laplace:

{displaystyle {frac {partial ^{2}u}{partial x^{2}}}+{frac {partial ^{2}u}{partial y^{2}}}=0.}

Non-linear partial derivative equation of third order, Korteweg-de Vries equation:

{displaystyle {frac {partial u}{partial t}}=6u{frac {partial u}{partial x}}-{frac {partial ^{3}u}{partial x^{3}}}.}

Exact Differential Equation Example

Be the first-order differential equation ${displaystyle P(x,y)dx+Q(x,y)dy=0}$ ${displaystyle forall (x,y)in B}$ where P and Q are two continuous functions in the open ${displaystyle Bsubset mathbb {R} ^{2}}$ .

It is said that the equation ${displaystyle P(x,y)dx+Q(x,y)dy=0}$ is an exact differential equation if there is a potential function ${displaystyle F(x,y)}$ defined in B such that:

${displaystyle {partial F over partial x}(x,y)=P(x,y)}$ ${displaystyle}$ ${displaystyle {partial F over partial y}(x,y)=Q(x,y)}$ ${displaystyle}$ ${displaystyle forall (x,y)in B}$

Be besides ${displaystyle P(x,y)dx+Q(x,y)dy=0}$ an exact differential equation ${displaystyle forall (x,y)in Bsubset mathbb {R} ^{2}}$ open and ${displaystyle F(x,y)}$ a potential function of this, then, every solution ${displaystyle y=phi (x)}$ of the equation whose graph is in B satisfies the equation

Solution of a differential equation

Existence of solutions

1st Step: Solving differential equations is not like solving algebraic equations. Since, although sometimes their solutions are unclear, it may also be of interest if they are unique or exist.

For first order problems with initial values, Peano's existence theorem gives us a set of conditions in which the solution exists. For any given point $(a,b)$ in the plane xy, and defined a rectangular region $Z$ , such that ${displaystyle Z=[l,m]times [n,p]}$ and $(a,b)$ is inside $Z$ . If we have a differential equation ${displaystyle {frac {mathrm {d} y}{mathrm {d} x}}=g(x,y)}$ and condition ${displaystyle y=b}$ When ${displaystyle x=a}$ , then there is a local solution to this problem if ${displaystyle g(x,y)}$ and ${displaystyle {frac {partial g}{partial x}}}$ are both continuous in $Z$ . The solution exists at some interval with your center in $a$ . The solution may not be unique. (See Ordinary differential equation for other results.)

However, this only helps us with first-order problems with initial conditions. Suppose we have a linear problem with initial conditions of nth order:

{displaystyle f_{n}(x){frac {mathrm {d} ^{n}y}{mathrm {d} x^{n}}}+cdots +f_{1}(x){frac {mathrm {d} y}{mathrm {d} x}}+f_{0}(x)y=g(x)}

such that

{displaystyle y(x_{0})=y_{0},y'(x_{0})=y'_{0},y''(x_{0})=y''_{0},cdots }

For any ${displaystyle f_{n}(x)}$ No, no. ${displaystyle {f_{0},f_{1},cdots }}$ and $g$ are continuous over some interval holding ${displaystyle x_{0}}$ , $y$ It is unique and exists.

Types of solutions

A solution of a differential equation is a function that, by replacing the unknown function, in each case with the corresponding derivations, verifies the equation, that is, converts it into an identity. There are three types of solutions:

General solution

The general solution is a generic solution, expressed with one or more constant. It's a curve beam. It has an infinity order according to its number of constants (a constant corresponds to a simply infinite family, two constants to a double-infinite family, etc.). In the event that the equation is linear, the general solution is achieved as a linear combination of the solutions (such as the order of the equation) of the homogeneous equation (which results from making the term not dependent on ${displaystyle y(x)}$ or its derivatives equal to 0) plus a particular solution to the complete equation

Particular solution

If you set any point ${displaystyle P(X_{0},Y_{0})}$ where the solution of the differential equation must necessarily pass, there is a single value of C, and therefore of the integral curve that satisfies the equation, it will receive the particular solution name of the equation at the point ${displaystyle P(X_{0},Y_{0})}$ which receives the initial condition name.

It is a particular case of the general solution, where the constant (or constants) receives a specific value.

Singular solution

The singular solution is a function that verifies the equation, but is not obtained by particularizing the general solution. It is a solution of the equation not consistent with a particular one of the general one, in other words, this solution does not belong to the general solution but still verifies the differential equation.

Notes on Solutions

Be the ordinary differential equation of order n ${displaystyle f(y^{(n)},y^{(n-1)},dotsy'',y',y,x)=0}$ , it's easy to verify that the function y= f(x) It's your solution. It is enough to calculate their derivatives of f(x), then replace them in the equation with f(x) and prove that an identity is obtained in x.

The solutions of E.D.O. they are presented in the form of implicitly defined functions, and sometimes impossible to express explicitly. For example

${displaystyle xy=ln y+c}$ which is a solution of: ${displaystyle {frac {{text{d}}y}{{text{d}}x}}={frac {y^{2}}{1-xy}}}$

The simplest form of all differential equations is ${displaystyle {text{d}}y/{text{d}}x=f(x)}$ whose solution is ${displaystyle y=int {f(x) {text{d}}x}+c}$ In some cases it is possible to solve it by elementary methods of calculation. However, in other cases, the analytical solution requires complex or more sophisticated variable techniques such as integrals:

${displaystyle y=int {exp(x^{2}) {text{d}}x}}$ and the integral ${displaystyle y=int {{frac {sin x}{x}} {text{d}}x}}$

cannot be structured by a finite number of elementary functions.

Applications

The study of differential equations is a vast field in pure and applied mathematics, physics, and engineering. All of these disciplines are interested in the properties of differential equations of various kinds. Pure mathematics focuses on the existence and uniqueness of solutions, while applied mathematics emphasizes the rigorous justification of solution approximation methods. Differential equations play a very important role in the virtual modeling of any physical, technical, or biological process, for example, both the celestial movement, the design of a bridge, or the interaction between neurons. The differential equations that are posed to solve real life problems are not necessarily directly solvable, that is, their solutions do not have a closed form expression. When this happens, the solutions can be approximated using numerical methods.

Many laws of physics and chemistry are formalized with differential equations. In biology and economics, differential equations are used for modeling the behavior of complex systems. The mathematical theory of differential equations was initially developed with the sciences where the equations originated and where results for applications were found. However, sometimes different problems arose in different scientific fields, resulting in identical differential equations. This happened because, behind the mathematical theory of the equations, a unified principle behind the phenomena can be seen. For example, if we consider the propagation of light and sound in the atmosphere, and of waves on the surface of a pond. All of these phenomena can be described with the same second-order partial differential equation, the wave equation, which allows us to think of light and sound as waveforms, and much like waves in water. Heat conduction, the theory that was developed by Joseph Fourier, is governed by another second-order partial derivative equation, the heat equation. It turns out that many diffusion processes, although they appear to be different, are described by the same equation. The Black-Scholes equation in finance, for example, is related to the heat equation.

Physics

Un ejemplo de solución para las ecuaciones en un atractor de Lorenz para el caso ρ = 28, σ = 10, y β = 8/3.

Equations of Euler-Lagrange in classical mechanics
Hamilton equations in classic mechanics
Radioactivity in nuclear physics
Newton cooling law in thermodynamics
Wave equation
Thermodynamic heat equation
Laplace equation, which defines harmonic functions
Poisson equation
Geodetic equation
Navier-Stokes equations in fluiddynamics
Dissemination equation in stochastic processes
Fluid-dynamic convection equation
Cauchy-Riemann equations in complex analysis
Poisson-Boltzmann equation in molecular dynamics
Equations of Saint-Venant
Universal differential equation
Equations of Lorenz whose solutions exhibit a chaotic flow.

Classical mechanics

Electrodynamics

General relativity

Quantum Mechanics

In quantum mechanics, the analogue to Newton's law is the Schrödinger Equation (a partial differential equation) for a quantized system (usually atoms, molecules, and subatomic particles that may be free, bound, or localized). It is not a simple algebraic equation, but it is, in general, a linear partial differential equation, describing the evolution in time of a wave function (also called a "state function").

Biology

Verhulst equation – for the growth of biological population.
Model von Bertalanffy – for individual biological growth.
Replication dynamic – in biological theory.
Hodgkin and Huxley Model – neuronal action potentials.

Predator-Prey Equations

The Lotka–Volterra equations, also known as the predator-prey equations, are a pair of first-order nonlinear differential equations frequently used to describe the dynamics of biological systems in which two species interact, one the predator, and one the predator. the other, the prey.

Population growth

Around the 18th century they wanted to know how the population varied to predict possible changes. That is why the economist T. Malthus proposes the following:

Births and deaths, at a small time interval, are proportional to the size of the population and the time interval.

It is imposed that ${displaystyle {text{nacimientos}}=alpha Delta tN(t)}$ and ${displaystyle {text{muertes}}=beta Delta tN(t)}$ with ${displaystyle N(t)=}$ size of the population in time t.

Variation of population at a time interval ${displaystyle {ce {Delta t}}}$ That's it. ${displaystyle Delta N(t)=gamma N(t)Delta t}$ with ${displaystyle gamma =alpha -beta }$ .

Using the limit when ${displaystyle Delta trightarrow 0}$ the mathematical model is obtained: ${displaystyle {dN over dt}=gamma N}$

By resolving the previous equation of separate variables, considering that $t=0$ the size of the population is ${displaystyle N_{0}}$ , you get the population in the instant t is given by ${displaystyle N(t)=N_{0}e^{gamma t}}$ . This equivalence reports, if $<math alttext="{displaystyle gamma γ γ .0{displaystyle gamma ₡0} <img alt="{displaystyle gamma$ the population is extinguished, if $gamma =0$ the population remains constant and $0}" xmlns="http://www.w3.org/1998/Math/MathML">γ γ ▪0{displaystyle gamma }0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/775a6435e4270cddf2cd7dcb486c20f7f4bb8cee" style="vertical-align: -0.838ex; width:5.523ex; height:2.676ex;"/>$ the population grows exponentially.

Values ${displaystyle {ce {N_0}}}$ and $gamma$ are calculated for each population taking two measures in two separate moments of time. It is important to note that a small error in the data count leads to different values of the constants $gamma$ or ${displaystyle N_{0}}$ which can be significant and significantly change the results of the model for large times.

Taking a real example. for the population in the USA we obtain:


Year	Population USA
1790	${displaystyle N(t)=3.9times 10^{6}e^{0.307t}}$
1800	${displaystyle N(t)=5.3times 10^{6}e^{0.307t}}$
1810	${displaystyle N(t)=7.2times 10^{6}e^{0.307t}}$
1820	${displaystyle N(t)=9.6times 10^{6}e^{0.307t}}$
1830	${displaystyle N(t)=12.9times 10^{6}e^{0.307t}}$
1840	${displaystyle N(t)=17.1times 10^{6}e^{0.307t}}$
1850	${displaystyle N(t)=23.2times 10^{6}e^{0.307t}}$
1860	${displaystyle N(t)=31.4times 10^{6}e^{0.307t}}$
1870	${displaystyle N(t)=38.6times 10^{6}e^{0.307t}}$
1880	${displaystyle N(t)=50.2times 10^{6}e^{0.307t}}$
1890	${displaystyle N(t)=62.9times 10^{6}e^{0.307t}}$
1900	${displaystyle N(t)=76times 10^{6}e^{0.307t}}$
1910	${displaystyle N(t)=92times 10^{6}e^{0.307t}}$
1920	${displaystyle N(t)=106.5times 10^{6}e^{0.307t}}$
1930	${displaystyle N(t)=123.2times 10^{6}e^{0.307t}}$

${displaystyle N(t)=}$ Verhulst proposes modifications to the Malthus model:

The population cannot grow unlimitedly but tends to stabilize at a limit ${displaystyle N_{infty }}$ and population variation is proportional to population N and factor ${displaystyle 1-{N over N_{infty }}}$ .

Therefore, the mathematical model tends to be: ${displaystyle {dN over dt}=gamma Nleft(1-{N over N_{infty }}right)}$ and, after making an integration of this model, you get the size of the population which is:

${displaystyle N(t)=}$ ${displaystyle N_{0}N_{infty } over {N_{0}+(N_{infty }-N_{0})e^{-gamma t}}}$

For the US population, the Verhulst values are calculated approximately:

${displaystyle N(t)=3.9times 10^{6}e^{0.307t}}$ , ${displaystyle N_{infty }=197times 10^{6}}$ and ${displaystyle gamma =0.3134}$ .

After comparing the values obtained with the Verhulst model with the real population, it can be seen that this slightly exceeds the amount predicted by the model and, therefore, there is the possibility of having to make some modification to said model in order to predict appropriately the size of the population for future times.

Software

ExpressionsinBar: desolve(y'=k*y,y)
Maple: dsolve
SageMath: desolve()
Xcas: desolve(y'=k*y,y)

Contenido relacionado

Más resultados...