Determinant (mathematics)

ImprimirCitar

In mathematics, the determinant is defined as an alternating multilinear form on a vector space. This definition indicates a series of mathematical properties and generalizes the concept of determinant of a matrix making it applicable in numerous fields. The concept of determinant or oriented volume was introduced to study the number of solutions of systems of linear equations.

History of determiners

Determinants were introduced to the West from the XVI century, that is, before matrices, which did not appear up to the 19th century. It was in China (Jiuzhang Suanshu) where a zero table was used for the first time and an algorithm was applied that, from the XIX century, is known as Gauss-Jordan elimination.^{[citation needed]}

The term matrix was created by James Joseph Sylvester trying to imply that it was “the mother of determiners”.^{[citation needed]}

Some of the greatest mathematicians of the 18th and 19th centuries contributed to the development of the properties of determinants. Most historians agree that the theory of determinants originated with the German mathematician Gottfried Wilhelm Leibniz (1646-1716). Leibniz used determinants in 1693 in relation to systems of simultaneous linear equations. However, there are those who believe that the Japanese mathematician Seki Kowa did the same a few years earlier.^{[citation needed]}

The most prolific contributions to the theory of the determinants were those of the French mathematician Agustin-Louis Cauchy (1789-1857). Cauchy wrote in 1812 a memory of 84 pages containing the first demonstration of the formula ${displaystyle det AB=det Adet B}$ .^{[chuckles]required]}

There are a few other mathematicians who deserve mention here. The development of a determinant by cofactors was first used by the French mathematician Pierre-Simon Laplace (1749-1827).^{[citation needed]}

A major contributor to the theory of determinants (with only Cauchy before him) was the German mathematician Carl Gustav Jacobi (1804-1851). It was he with whom the word "determinant" gained final acceptance. Sylvester later called this determinant Jacobian.^{[citation needed]}

First calculations of determinants

In its original sense, the determinant determines the uniqueness of the solution of a system of linear equations. It was introduced for the case of order 2 by Cardano in 1545 in his work Ars Magna as a rule for solving systems of two equations in two unknowns. This first formula bears the name of regula de modo.

The Japanese Kowa Seki introduced the determinants of order 3 and 4 at the same time as the German Leibniz.

The appearance of determinants of higher orders still took more than a hundred years to arrive. Curiously, the Japanese Kowa Seki and the German Leibniz gave the first examples almost simultaneously.

Leibniz studied the different types of linear equation systems. In the absence of a matrix notation, he represented the coefficients of the unknowns with a couple of indices: so he wrote ij to represent $a_{ij}$ . In 1678, he was interested in a system of three equations with three unknowns and obtained, for example, the development formula along a column. The same year, he wrote a determinant of order 4, correct in everything except in the sign. Leibniz did not publish this work, which seemed to be forgotten until the results were rediscovered independently fifty years later.

In the same period, Kowa Seki published a manuscript on determiners, where general formulas difficult to interpret are found. Correct formulas seem to be given for determinants of order 3 and 4, and again the signs are wrong for the determinants of larger size. which is reflected in the expulsion of the Jesuits in 1638.

Determinants of any dimension

In 1748, in a posthumous treatise on algebra by MacLaurin, the rule appears to obtain the solution of a system of n linear equations with n unknowns when n is 2, 3, or 4, through the use of determiners. In 1750, Cramer gives the rule for the general case, though he offers no proof. The calculation methods of the determinants are so far delicate because they are based on the notion of signature of a permutation.

Mathematicians become familiar with this new object through papers by Bézout in 1764, by Vandermonde in 1771 (which specifically provide the calculation of the determinant of the current Vandermonde matrix). In 1772, Laplace established the recurrence rules that bear his name. In the following year, Lagrange discovers the relationship between the calculation of determinants and that of volumes.

Gauss used the term «determinant» for the first time, in the Disquisitiones arithmeticae in 1801. He used it for what we now call the discriminant of a quadric and which is a particular case of a modern determinant. He likewise came close to obtaining the theorem of the determinant of a product.

Emergence of the modern notion of determinant

Cauchy was the first to use the term determiner in its modern meaning. He was in charge of carrying out a synthesis of previous knowledge and published in 1812 the formula and proof of the determinant of a product along with the statement and proof of Laplace's rule. That same year Binet offered another (incorrect) proof for the formula of the determinant of a product. At the same time, Cauchy establishes the bases of the study of the reduction of endomorphisms.

In 1825 Heinrich F. Scherk published new properties of determinants. Among the properties found was the property that in a matrix in which a row is a linear combination of several other rows in the matrix, the determinant is zero.

With the publication of his three treatises on determiners in 1841 in Crelle's magazine, Jacobi brought the notion a great notoriety. He for the first time he presents systematic calculation methods in an algorithmic form. In the same way, he makes possible the evaluation of the determinant of functions with the definition of the Jacobian, which supposes a great advance in the abstraction of the concept of the determinant.

The matrix table is introduced by the works of Cayley and James Joseph Sylvester^{[citation needed]}. Cayley is also the inventor of the notation of determinants using vertical bars (1841) and establishes the formula for calculating the inverse of a matrix using determinants (1858).

The theory is reinforced by the study of determinants that have particular symmetry properties and by the introduction of the determinant into new fields of mathematics, such as the Wronskian in the case of linear differential equations.

Calculation methods

Main articles: Theorem of Laplace and Rule of Sarrus.

For the calculation of determinants of matrices of any order, there is a recursive rule (Laplace's theorem) that reduces the calculation to additions and subtractions of several determinants of a lower order. This process can be repeated as many times as necessary until the problem is reduced to the calculation of multiple determinants of order as small as desired. Knowing that the determinant of a scalar is the scalar itself, it is possible to calculate the determinant of any matrix applying said theorem.

In addition to this rule, to calculate determinants of matrices of any order we can use another definition of determinant known as the Leibniz Formula.

The Leibniz formula for the determinant of a square matrix A of order n is:

${displaystyle det A=sum _{sigma in P_{n}}operatorname {sgn}(sigma)prod _{i=1}^{n}a_{i,sigma _{i}}}$ ,

where the sum is calculated on all the permutations σ of the whole {1,2,...n}. The position of the element i after permutation σ is denoted as σ_i. The set of all permutations is ${displaystyle P_{n}}$ . For each σ, sgn(σ) is the Symbol σ, this is +1 if the permutation is pair and −1 if it is unstoppable (see Permutation Parity).

In any of the $n!$ the term

{displaystyle prod _{i=1}^{n}a_{i,sigma _{i}} }

denotes the product of the entries at position (i, σ_i), where i goes from 1 to n:

{displaystyle a_{1,sigma _{1}}cdot a_{2,sigma _{2}}cdots a_{n,sigma _{n}}. }

Leibniz's formula is useful as a definition of a determinant; but, except for very small orders, this is not a practical way to calculate it: you have to carry out n! products of n factors and add n! items. It is not normally used to calculate the determinant if the matrix has more than three rows.

Lower-order matrices

The case of matrices of lower order (order 1, 2 or 3) is very simple and its determinant is calculated with simple known rules. These rules are also deducible from Laplace's theorem.

A matrix of order one, is a trivial case, but we will treat it to complete all cases. A matrix of order one can be treated as a scalar, but here we will consider it a square matrix of order one:

{displaystyle A=left[{begin{array}{c}a_{11}end{array}}right]}

The value of the determinant is equal to the only term of the matrix:

{displaystyle det A=det left[{begin{array}{c}a_{11}end{array}}right]=a_{11}}

The determinant of a matrix of order 2:

{displaystyle A=left[{begin{array}{cc}a_{11}&a_{12}\a_{21}&a_{22}end{array}}right]}

are calculated with the following formula:

{displaystyle |A|={begin{vmatrix}a_{11}&a_{12}\a_{21}&a_{22}end{vmatrix}}=a_{11}a_{22}-a_{12}a_{21}}

Given a matrix of order 3:

{displaystyle A=left[{begin{array}{ccc}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{array}}right]}

The determinant of a matrix of order 3 is calculated using the Sarrus rule:

{displaystyle |A|=left|{begin{array}{ccc}a_{11}&a_{12}&a_{13}\a_{21}&a_{22}&a_{23}\a_{31}&a_{32}&a_{33}end{array}}right|=(a_{11}a_{22}a_{33}+a_{12}a_{23}a_{31}+a_{13}a_{21}a_{32})-(a_{31}a_{22}a_{13}+a_{32}a_{23}a_{11}+a_{33}a_{21}a_{12})}

Higher Order Determinants

The determining order n, can be calculated using the Laplace theorem from a row or column, reducing the problem to the calculation of n determinants of order n-1. To do this you take a row or column any, multiplying each element by its cofactor. The cofactor of an element ${displaystyle a_{ij}}$ of the matrix is the determinant of the matrix that is obtained by removing the row and column corresponding to that element, and multiplying it by (-1)^i+jwhere i is the row number and j the column number. The sum of all products of the elements of a row (or column) any multiplied by their cofactors is equal to the determinant.

In the case of a determinant of order 4, determinants of order 3 are directly obtained that can be calculated by the Sarrus rule. On the other hand, in higher order determinants, such as n = 5, when developing the elements of a line, we will obtain order 4 determinants, which in turn must be developed by the same method, to obtain order 3 determinants For example, to obtain a determinant of order 4 with the specified method, 4 determinants of order 3 must be calculated. since the other determinants will be multiplied by 0, which cancels them).

The amount of operations increases very quickly. For example, using this method, for a determinant of order 10, 10 x 9 x 8 x 7 x 6 x 5 x 4 = 604,800 determinants of order 3 must be calculated.

You can also use the Gaussian Elimination Method, to convert the matrix to a triangular matrix.

Numerical methods

To reduce the computational cost of the determinants while improving their stability against rounding errors, Chio's rule is applied, which allows the use of matrix triangularization methods, thereby reducing the calculation of the determinant to the product of the diagonal elements of the resulting matrix. Any known method that is numerically stable can be used for triangularization. These are usually based on the use of orthonormal matrices, such as the Gaussian method or the use of Householder reflections or Givens rotations.

Determinants in infinite dimension

Under certain conditions the determinant of linear maps of an infinite-dimensional Banach vector space can be defined. Specifically in the determinant it is defined for the operators of the determinant class that can from the operators of the trace class. A notable example was the Fredholm determinant which he defined in connection with his study of the integral equation named after him:

(♪) ${displaystyle f(x)=phi (x)+int _{0}^{1}K(x,y)phi (y) dy}$

Where:

f(x),

It's a known function.

{displaystyle phi (x),}

It's an unknown function.

{displaystyle K(x,y),}

is a known function called core, which gives rise to the next compact linear operator and finite trace in the Hilbert space of integrated square functions in the interval [0.1]:

{displaystyle {hat {K}}:L^{2}[0,1]to L^{2}[0,1],quad ({hat {K}}phi)(x)=int _{0}^{1}K(x,y)phi (y) dy}

The equation (♪) has solution if the determinant of Fredholm ${displaystyle det(I+{hat {K}})}$ It's not annulled. The determinant of Fredholm in this case generalizes the determinant in finite dimension and can be calculated explicitly by:

${displaystyle det(I+{hat {K}})=sum _{k=0}^{infty }{frac {1}{k!}}int _{0}^{1}dots int _{0}^{1}det[K(x_{i},x_{j})]_{1leq i,jleq k} dx_{1}dots dx_{k}}$

The solution of the equation (*) can be simply written in terms of the determinant when it does not vanish.

First Examples: Areas and Volumes

The calculation of areas and volumes in the form of determinants in Euclidean spaces appear as particular cases of a more general notion of determinant. The capital letter D (Det) is sometimes reserved to distinguish them.

Determinant of two vectors in the Euclidean plane

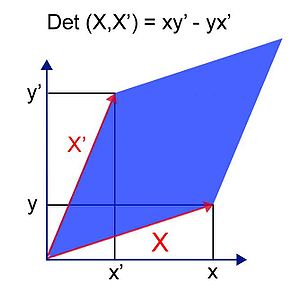
Fig. 1. The determinant is the oriented blue area.

Let P be the Euclidean plane. The determinant of the vectors X and X' is obtained with the analytic expression

{displaystyle det(X,X')={begin{vmatrix}x&x'\y&y'end{vmatrix}}=xy'-yx'}

or, equivalently, by the geometric expression

{displaystyle det(X,X')=|X|cdot |X'|cdot sin theta }

in which $theta$ is the angle oriented by the vectors X and X'.

Properties

The absolute value of the determinant is equal to the surface of the parallelogram defined by X and X' ( ${displaystyle X'sin theta }$ is in fact the height of the parallelogram, so A = Base × Height.
The determinant is zero if and only if the two vectors are colinear (the parallelogram becomes a line).
Your sign is strictly positive if and only if the angle measurement (X, X ') is in ]0, $pi$ [.
The application of the determinant is bilinear: the linearity regarding the first vector is written

{displaystyle det(aX+bY,X')=adet(X,X')+bdet(Y,X');}

y about the second

{displaystyle det(X,aX'+bY')=adet(X,X')+bdet(X,Y');}

Fig. 2.Suma of two adjacent parallel areas.

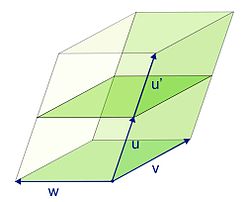
Figure 2, on the plan, illustrates a particular case of this formula. Represents two adjacent parallelograms, one defined by the vectors u and v (in green), and the other by the vectors u' and v (in blue). It is easy to see on this example the area of the parallelogram defined by the vectors u+u' and v (in gray): it is equal to the sum of the two preceding parallelograms to which the area of a triangle is subtracted and the area of another triangle is added. Both triangles correspond by translation and the following formula is verified Det (u+u', v)=Det (u, v)+Det (u', v).

The drawing corresponds to a particular case of the bilinearity formula since the orientations have been chosen so that the areas have the same sign, although it helps to understand the geometric content.

Generalization

It is possible to define the notion of determinant in an oriented Euclidean plane with a direct orthonormal basis B using the coordinates of the vectors in this basis. The calculation of the determinant gives the same result regardless of the direct orthonormal basis chosen for the calculation.

Determinant of three vectors in Euclidean space

Let E be the oriented Euclidean space of dimension 3. The determinant of three vectors of E is given by

{displaystyle det(X,X',X'')={begin{vmatrix}x&x'&x''\y&y'&y''\z&z'&z''end{vmatrix}}=x{begin{vmatrix}y'&y''\z'&z''end{vmatrix}}-x'{begin{vmatrix}y&y''\z&z''end{vmatrix}}+x''{begin{vmatrix}y&y'\z&z'end{vmatrix}}=xy'z''+x'y''z+x''yz'-xy''z'-x'yz''-x''y'z.}

Fig. 3. Graphical illustration of trilineality.

This determinant is called the mixed product.

Properties

The absolute value of the determinant is equal to the volume of parallelopipe defined by the three vectors.
The determinant is zero if and only if the three vectors are in the same plane (paralepipe "plane").
The determining application is trilinear: above all

{displaystyle det(aX+bY,X',X'')=adet(X,X',X'')+bdet(Y,X',X''),}

A geometric illustration of this property is given in figure 3 with two adjacent parallelepipeds, that is, with a common face. The following equality is then intuitive:

{displaystyle det(u+u',v,w)=det(u,v,w)+det(u',v,w),}

Properties

The determinant of a matrix is an algebraic invariant, which implies that given a linear application all the matrices that represent it will have the same determinant. This allows to define the value of the determinant not only for matrices but also for linear applications.
The determinant of a matrix and the determinant of its transplant match: ${displaystyle det(A^{t})=det(A),}$

A linear application between vectorial spaces is invertible if and only if its determinant is not null. Therefore, a matrix with coefficients in a body is invertible if and only if its determinant is not null.

Determinant of the product

A fundamental property of the determinant is its multipliative behavior against the product of matrices:

${displaystyle det mathbf {AB} =det mathbf {A} cdot det mathbf {B} }$

This property is more transcendent than it seems and is very useful in calculating determinants. In fact, suppose we want to calculate the determinant of the matrix ${mathbf {A}}$ and that ${displaystyle mathbf {U} }$ is any matrix with determining one (the neutral element regarding the body's product). In this case, it is verified that:

${displaystyle det mathbf {A} =det mathbf {A} cdot det mathbf {U} =det mathbf {AU} }$

and similarly ${displaystyle det mathbf {A} =det mathbf {UA} }$ ,

A linear application between two finite dimension vector spaces can be represented by a matrix. The matrix associated with the composition of linear applications between finite dimension spaces can be calculated using the matrices product. Two linear applications $u,$ and $v,$ the following is fulfilled:

${displaystyle det(ucirc v)=det(u)cdot det(v)}$

Arrays in blocks

Sean. ${displaystyle A,B,C,D}$ size matrices ${displaystyle ntimes n,ntimes m,mtimes n,mtimes m}$ respectively. Then

${displaystyle det left[{begin{array}{cc}A&0\C&Dend{array}}right]=det left[{begin{array}{cc}A&B\0&Dend{array}}right]=det Acdot det D}$ .

This can be seen from Leibniz's formula. Using the following identity

{displaystyle left[{begin{array}{cc}A&B\C&Dend{array}}right]=left[{begin{array}{cc}A&0\C&Iend{array}}right]times left[{begin{array}{cc}I&A^{-1}B\0&D-CA^{-1}Bend{array}}right]}

we see that for an invertible matrix A, it is

{displaystyle det left[{begin{array}{cc}A&B\C&Dend{array}}right]=det Acdot det(D-CA^{-1}B)}

Similarly, a similar identity can be obtained with ${displaystyle det D}$ factored.

Yeah. ${displaystyle d_{ij}}$ They're diagonal matrices,

{displaystyle det left|{begin{array}{ccc}d_{11}&ldots &d_{1c}\vdots &&vdots \d_{r1}&ldots &d_{rc}end{array}}right|=det left|{begin{array}{ccc}det(d_{11})&ldots &det(d_{1c})\vdots &&vdots \det(d_{r1})&ldots &det(d_{rc})end{array}}right|.}

Derivative of the determining function

The determining function can be defined on the vector space formed by the square matrices of order n. Said vector space can easily be converted into a normed vector space by means of the matrix norm, thanks to which said space becomes a metric and topological space, where limits can be defined. The determinant can be defined as a morphism from the algebra of matrices to the set of elements of the field on which the matrices are defined:

${displaystyle det:M_{ntimes n}(mathbb {K})to mathbb {K} }$

The differential of the determining function is given in terms of the adjoint matrix:

${displaystyle {frac {partial det(mathbf {A})}{partial mathbf {H} }}:=D(det)|_{mathbf {A} }(mathbf {H})=lim _{epsilon to 0}{frac {det(mathbf {A+epsilon H})-det(mathbf {A})}{epsilon }}={mbox{tr}}left({mbox{adj}}(mathbf {A}) mathbf {H} right)}$

Where:

{displaystyle {mbox{adj}}(mathbf {A})}

is the attachment matrix.

{displaystyle {mbox{tr}}(cdot)}

It's the matrix trace.

Children of an array

Main article: Minor (linear algebra)

In addition to the determinant of a square matrix, given a matrix other quantities can be defined by the use of determinants related to the algebraic properties of that matrix. Specifically given a square or rectangular matrix you can define the so-called determinants minors r from the determinant of square submatrics of rxr of the original matrix. Given the matrix ${displaystyle mathbf {A} =[a_{ij}]}$ :

${displaystyle mathbf {A} ={begin{bmatrix}a_{11}&dots &a_{1n}\dots &dots &dots \a_{m1}&dots &a_{mn}end{bmatrix}}}$

Anything less than rank r is defined as:

$<math alttext="{displaystyle {begin{vmatrix}a_{i_{1}j_{1}}&dots &a_{i_{1}j_{r}}\dots &dots &dots \a_{i_{r}j_{1}}&dots &a_{i_{r}j_{r}}end{vmatrix}},qquad {begin{cases}1leq i_{1}<i_{2}<dots <i_{r}leq n\1leq j_{1}<j_{2}<dots 日本語ai1j1...... ai1jr...... ...... ...... airj1...... airjr日本語,{1≤ ≤ i1.i2. .ir≤ ≤ n1≤ ≤ j1.j2. .jr≤ ≤ m### #################################################################################################################################### ######################################################################################################################<img alt="{displaystyle {begin{vmatrix}a_{i_{1}j_{1}}&dots &a_{i_{1}j_{r}}\dots &dots &dots \a_{i_{r}j_{1}}&dots &a_{i_{r}j_{r}}end{vmatrix}},qquad {begin{cases}1leq i_{1}<i_{2}<dots <i_{r}leq n\1leq j_{1}<j_{2}<dots$

Note that in general there will be a large number of minors of order r, in fact the number of minors of order r of a matrix mxn is given by:

${displaystyle {mbox{Min}}_{r}^{mtimes n}={m choose r}{n choose r}}$

An interesting property is that the range coincides with the order of the largest possible non-zero minor, being the calculation of minors one of the most used means to calculate the range of a matrix or of a linear map.

Contenido relacionado

Más resultados...

Determinant (mathematics)

History of determiners

First calculations of determinants

Determinants of any dimension

Emergence of the modern notion of determinant

Calculation methods

Lower-order matrices

Higher Order Determinants

Numerical methods

Determinants in infinite dimension

First Examples: Areas and Volumes

Determinant of two vectors in the Euclidean plane

Properties

Generalization

Determinant of three vectors in Euclidean space

Properties

Properties

Determinant of the product

Arrays in blocks

Derivative of the determining function

Children of an array

Contenido relacionado

Factorial

Paraboloid

Hamming distance