Derivative

ImprimirCitar

The derivative of the function at the marking point is equivalent to the slope of the tangent line.

In differential calculus and mathematical analysis, the derivative of a function is the instantaneous rate of change with which the value of said mathematical function varies, as the value of its independent variable changes. The derivative of a function is a local concept, that is, it is calculated as the limit of the average rate of change of the function in a certain interval, when the interval considered for the independent variable becomes smaller and smaller. talks about the value of the derivative of a function at a given point.

A common example appears when studying motion: if a function represents the position of an object with respect to time, its derivative is the velocity of that object for all moments. An airplane making a 4,500 km transatlantic flight between 12:00 and 18:00 travels at an average speed of 750 km/h. However, you may be traveling at higher or slower speeds on different sections of the route. In particular, if between 3:00 p.m. and 3:30 p.m. you travel 400 km, your average speed in that section is 800 km/h. To know your instantaneous speed at 15:20, for example, it is necessary to calculate the average speed in smaller and smaller time intervals around this time: between 15:15 and 15:25, between 15:19 and 15:21.

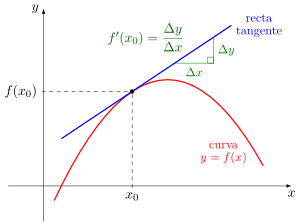
Then the value of the derivative of a function at a point can be interpreted geometrically, since it corresponds to the slope of the tangent line to the graph of the function at that point. The tangent line is, in turn, the graph of the best linear approximation of the function around said point. The notion of derivative can be generalized for the case of functions of more than one variable with the partial derivative and the differential.

History of the derivative

The typical problems that gave rise to the infinitesimal calculus began to be posed in the classical age of ancient Greece (III century century). B.C.), but no systematic resolution methods were found until nineteen centuries later (in the XVII century by Isaac Newton and Gottfried Leibniz).

As far as derivatives are concerned, there are two concepts of a geometric type that gave rise to them:

The problem of tangent to a curve (Apolonio de Perge)
The Theorem of the extremes: maximum and minimum (Pierre de Fermat)

Together they gave rise to what is now known as differential calculus.

17th century

Mathematicians lost the fear that the Greeks had of infinitesimals: Johannes Kepler and Bonaventura Cavalieri were the first to use them, they began to walk a path that would lead in half a century to the discovery of calculus.

In the middle of the XVII century the infinitesimal quantities were increasingly used to solve problems of calculations of tangents, areas, volumes; The first would give rise to the differential calculus, the others to the integral.

Newton and Leibniz

Main articles: Isaac Newton and Gottfried Leibniz.

At the end of the XVII century the algorithms used by their predecessors were synthesized in two concepts, in what we now call « derivative” and “integral”. The history of mathematics recognizes that Isaac Newton and Gottfried Leibniz are the creators of the differential and integral calculus. They developed rules for manipulating derivatives (derivation rules) and Isaac Barrow showed that differentiation and integration are inverse operations.

Newton developed his own method for calculating tangents in Cambridge. In 1665 he found an algorithm for deriving algebraic functions that matched the one discovered by Fermat. At the end of 1665 he dedicated himself to restructuring the bases of his calculation, trying to break away from the infinitesimals, and introduced the concept of fluxion, which for him was the speed with which a variable "flows" (varies) over time.

Gottfried Leibniz, for his part, formulated and developed the differential calculus in 1675. He was the first to publish the same results that Isaac Newton discovered 10 years earlier, independently. In his research, he kept a geometric character and treated the derivative as an incremental quotient and not as a speed, seeing the meaning of its correspondence with the slope of the tangent line to the curve at said point.

Leibniz is the inventor of various mathematical symbols. To it are the names of: differential calculation and integral calculation, as well as derivative symbols $textstyle {frac {mathrm {d} y}{mathrm {d} x}}$ and the symbol of the integral ∫.

Concepts and applications

The concept of derivative is one of the basic concepts of mathematical analysis. The others are those of definite and indefinite integral, sequence; above all, the concept of limit. This is used for the definition of any type of derivative and for the Riemann integral, convergent sequence and sum of a series and continuity. Due to its importance, there is a before and after of such a concept that bisects previous mathematics, such as algebra, trigonometry or analytical geometry, of calculus. According to Albert Einstein, the greatest contribution obtained from derivatives was the possibility of formulating various problems in physics using differential equations ^{[citation required]}.

The derivative is a concept that has varied applications. It is applied in cases where it is necessary to measure the speed with which a change of magnitude or situation occurs. It is a fundamental calculation tool in the studies of Physics, Chemistry and Biology, or in social sciences such as Economics and Sociology. For example, when referring to the two-dimensional graph $f$ , is considered the derivative as the slope of the tangent line of the graph at the point $x$ . You can approach the slope of this tangent as the limit when the distance between the two points that determine a secant straight tends to zero, that is, the secant straight is transformed into a tangent line. With this interpretation, many geometric properties of function graphics can be determined, such as monotony of a function (if it is growing or decreasing) and concavity or convexity.

Some functions do not have a derivative at all or at some of their points. For example, a function has no derivative at points where it has a vertical tangent, a discontinuity, or an angular point. Fortunately, many of the functions that are considered in practical applications are continuous and their graph is a smooth curve, so they are susceptible to differentiation.

Functions that are differentiable (differentiable if speaking in a single variable), are linearly approximable.

Derivative Definitions

Derivative at a point from differential quotients

Secant recipe between f(x) and f(x+h)

The derivative of a function $f,$ at the point $a$ is the slope of the tangent line to the graph of $f,$ at the point $a,$ . The value of this slope will be approximately equal to the slope of a dry straight to the graph passing by the point ${displaystyle (a,f(a))}$ and by a nearby point $(x,f(x))$ ; for convenience it is often expressed ${displaystyle x=a+h}$ Where $h$ is a number close to 0. From these two points the slope of the secant straight is calculated as

{displaystyle {frac {f(x)-f(a)}{x-a}}={frac {f(a+h)-f(a)}{h}}.}

(This expression is called "differential quotient" or "Newton quotient"). As the number $h$ near zero, the value of this slope will be closer to that of the tangent line. This allows to define derivative of the function $f$ at the point $a$ , denoted as ${displaystyle f'(a)}$ like the limit of these quotients when $h$ tends to zero:

{displaystyle f'(a)=lim _{hto 0}{frac {f(a+h)-f(a)}{h}}}

However, this definition is only valid when the limit is a real number: at points $a$ where the limit does not exist, the function $f$ It has no derivative.

Inclination of the drying of the curve and=f(x)

Derivative of a function

An animation that gives an intuitive idea of the derivative, since the «swing» of a function changes when the argument changes.

Given a function $f$ , you can define a new function that, at each point $x$ , takes the value of the derivative ${displaystyle f'(x)}$ . This function is denoted $f'$ and called derivative function of $f$ or simply derivative of $f$ . This is, the derivative of $f$ is the function given by

{displaystyle f'(x)=lim _{hto 0}{frac {f(x+h)-f(x)}{h}}}

This function is only defined in the domain points $f$ where the limit exists; in other words, the domain of $f'$ is contained in the $f$ .

Examples

Consider quadratic function ${displaystyle f(x)=x^{2}}$ defined for all $xinmathbb{R}$ . It is a matter of calculating the derivative of this function by applying the definition

{displaystyle {begin{aligned}f'(x)&=lim _{hto 0}{frac {(x+h)^{2}-x^{2}}{h}}\&=lim _{hto 0}{frac {x^{2}+2xh+h^{2}-x^{2}}{h}}\&=lim _{hto 0}{frac {2xh+h^{2}}{h}}\&=lim _{hto 0}(2x+h)\&=2x.end{aligned}}}

For the general case

{displaystyle g(x)=x^{n}}

We'd have to.

{displaystyle g'(x)=lim _{hto 0}{frac {(x+h)^{n}-x^{n}}{h}}}

Taking into account the theorem of the binomial;

{displaystyle (x+h)^{n}=sum _{k=0}^{n}{binom {n}{k}}x^{n-k}h^{k}={binom {n}{0}}x^{n}+{binom {n}{1}}x^{n-1}h+{binom {n}{2}}x^{n-2}h^{2}+cdots +{binom {n}{n-1}}xh^{n-1}+{binom {n}{n}}h^{n}}

We have;

{displaystyle {begin{aligned}g'(x)&=lim _{hto 0}{frac {{binom {n}{0}}x^{n}+{binom {n}{1}}x^{n-1}h+{binom {n}{2}}x^{n-2}h^{2}+cdots +{binom {n}{n-1}}xh^{n-1}+{binom {n}{n}}h^{n}-x^{n}}{h}}\&=lim _{hto 0}{frac {x^{n}+nx^{n-1}h+{frac {n(n-1)}{2}}x^{n-2}h^{2}+cdots +nxh^{n-1}+h^{n}-x^{n}}{h}}\&=lim _{hto 0}{frac {x^{n}+h(nx^{n-1}+{frac {n(n-1)}{2}}x^{n-2}h+cdots +nxh^{n-2}+h^{n-1})-x^{n}}{h}}\&=lim _{hto 0}nx^{n-1}+{frac {n(n-1)}{2}}x^{n-2}h+cdots +nxh^{n-2}+h^{n-1}=nx^{n-1}end{aligned}}}

Continuity and differentiability

Main article: Continuous function

Continuity is necessary

For a function to be derivable at a point it is also necessary to be continuous at that point: intuitively, if the graph of a function is "rotate" at a point, there is no clear way to trace a tangent line to the graph. More precisely, this is because, if a function $f$ is not continuous at a point $a$ , then the difference between the value ${displaystyle f(a)}$ and value at a nearby point ${displaystyle f(a+h)}$ is not going to tend to 0 as the distance $h$ between the two points tends to 0; in fact, the limit ${displaystyle lim _{hto 0}f(a+h)-f(a)}$ it doesn't have to be well defined if the two lateral limits are not equal. Whether this limit does not exist as if it exists but is different from 0, the differential ratio

{displaystyle {frac {f(a+h)-f(a)}{h}}}

will not have a defined boundary.

The function of Heaviside is not continuous

x=0

As an example of what happens when the function is not continuous, consider the Heaviside function, defined as

<math alttext="{displaystyle f(x)=left{{begin{array}{ll}1,&{text{si }}xgeq 0\0,&{text{si }}xf(x)={1,Yeah.x≥ ≥ 00,Yeah.x.0.{displaystyle f(x)=left{begin{array}{ll}{ll}1, stranger{text{si}xgeq 0\0, stranger{text{si }}}{x.end{array}}right. !<img alt="{displaystyle f(x)=left{{begin{array}{ll}1,&{text{si }}xgeq 0\0,&{text{si }}x

This function is not continuous $x=0$ : the function value at this point is 1, but at all points to your left the function is 0. In this case, the limit on the left of the difference ${displaystyle lim _{hto 0^{-}}f(0+h)-f(0)}$ is equal to 1, so the differential quotient will not have a well defined limit.

Continuity is not enough

The absolute value function is not derived at the point

x=0

The relation does not work inversely: the fact that a function is continuous does not guarantee its differentiability. It is possible that the lateral limits are equal but the lateral derivatives are not; in this specific case, the function presents an angular point at that point.

An example is the absolute value function ${displaystyle f(x)=|x|}$ which is defined as

<math alttext="{displaystyle |x|=left{{begin{array}{rl}x,&{text{si }}xgeq 0\-x,&{text{si }}x日本語x日本語={x,Yeah.x≥ ≥ 0− − x,Yeah.x.0.{displaystyle Șx=left{begin{array}{rl}{rl}x, fake{text{si}xgeq 0-x, fake{text{si }}}}{end{array}right. !<img alt="{displaystyle |x|=left{{begin{array}{rl}x,&{text{si }}xgeq 0\-x,&{text{si }}x

This function is continuous at the point $x=0$ : at this point the function takes the value 0, and for values $x$ infinitely close to 0, both positive and negative, the value of the function tends to 0. However, it is not derivable: the lateral derivative on the right of $x=0$ is equal to 1, while on the left the lateral derivative is worth -1. Since the lateral derivatives give different results, there is no derivation $x=0$ even though the function is continuous at that point.

Informally, if the graph of the function has sharp points, breaks off, or has jumps, it is not differentiable. However, the function f(x)=x|x| is differentiable for all x.

Notation

There are various ways to name the derivative. Being f a function, the derivative of the function is written $f,$ value $x,$ in several ways.

Lagrange notation

The simplest notation for differentiation, in current use, is due to Lagrange, and consists of denoting the derivation of a function $f(x)$ Like ${displaystyle f'(x)}$ : read "f prima de x". This notation extends to derivatives of superior order, giving rise to ${displaystyle f''(x)}$ (“f second of x” or “f two premium of x”) for the second derivative, and ${displaystyle f'''(x)}$ for the third derivative. The fourth and following derivatives can be described in two ways:

with Roman numerals: ${displaystyle f^{text{IV}}(x)}$ ,
with numbers in parentheses: ${displaystyle f^{(4)}(x)}$ .

This last option also gives rise to notation ${displaystyle f^{(n)}(x)}$ to denote the derivative n-thousand of $f$ .

Leibniz Notation

Main article: Notation of Leibniz

Another common notation for differentiation is due to Leibniz. For the derivative function $f,$ , it is written:

{displaystyle {frac {dleft(f(x)right)}{dx}}.}

It can also be found as $textstyle {frac {mathrm {d} y}{mathrm {d} x}}$ , $textstyle {frac {mathrm {d} f}{mathrm {d} x}}$ or $textstyle {frac {mathrm {d} }{mathrm {d} x}}f(x)$ . It reads “defeated $y,$ ( $f,$ or $f,$ of $x,$ ) regarding $x,$ ». This notation has the advantage of suggesting to the derivative of one function with respect to another as a differential quotient.

With this notation, you can write the derivative $f$ at the point $a$ in two different ways:

{displaystyle left.{frac {df}{dx}}right|_{x=a}=left({frac {dleft(f(x)right)}{dx}}right)(a).}

Yeah. ${displaystyle y=f(x),}$ , you can write the derivative as

{displaystyle {frac {dy}{dx}}}

Successive derivatives are expressed as

{displaystyle {frac {d^{n}f}{dx^{n}}}}

{displaystyle {frac {d^{n}y}{dx^{n}}}}

for the enseima derived from $f,$ or $y$ respectively. Historically, this comes from the fact that, for example, the third derivative is

{frac {mathrm {d} left({frac {mathrm {d} left({frac {mathrm {d} left(f(x)right)}{mathrm {d} x}}right)}{mathrm {d} x}}right)}{mathrm {d} x}}

which can be written as

left({frac {mathrm {d} }{mathrm {d} x}}right)^{3}left(f(x)right)={frac {mathrm {d} ^{3}}{left(mathrm {d} xright)^{3}}}left(f(x)right).

Leibniz's notation is very useful, as it allows you to specify the difference variable (in the denominator); which is relevant in case of partial differentiation. It also makes it easier to remember the chain rule, because the d-terms seem to symbolically cancel:

{frac {mathrm {d} y}{mathrm {d} x}}={frac {mathrm {d} y}{mathrm {d} u}}cdot {frac {mathrm {d} u}{mathrm {d} x}}.

In the popular formulation of calculus by limits, the d-terms cannot literally cancel, because they are themselves undefined; they are defined only when used together to express a derivative. In non-standard analyses, however, one can see infinitesimal numbers canceling out.

Indeed, Leibnitz (did) consider the derivative dy/dx to be the quotient of two “infiniteths” dy and dx , called “spreads”. These infinitesimals were not numbers but quantities smaller than any positive number.

Newton's Notation

Main article: Newton score

Newton's notation for differentiation with respect to time, was to put a dot above the name of the function:

{displaystyle {dot {x}}=x^{prime }(t)}

{ddot {x}}=x^{prime prime }(t)

and so on.

It is read «point $x,$ » or « $x,$ point». It is currently disused in the area of pure mathematics, however it is still used in areas of physics as mechanics, where other notations of the derivative can be confused with relative speed notation. It is used to define the temporary derivative of a variable.

This Newton notation is used mainly in mechanics, usually for derivatives involving the variable time, as an independent variable; such as velocity and acceleration, and in theory of ordinary differential equations. It is usually only used for the first and second derivatives.

Euler's Notation

mathrm {D} _{x}f,

partial _{x}f,

(Notations of Euler and Jacobi, respectively)

read « $d,$ sub $x,$ of $f,$ », and D and φ symbols should be understood as differential operators.

Calculation of the derivative

The derivative of a function, in principle, can be calculated from the definition, expressing the quotient of differences and calculating its limit. However, except for a few cases this can be laborious. In practice there are pre-qualified formulas for those derived from the simplest functions, while for the most complicated functions a number of rules are used to reduce the problem to the calculation of the derivative of simpler functions. For example, to calculate the derivative of the function ${displaystyle cos(x^{2})}$ it would be enough to know: $x^{2}$ , the derivative ${displaystyle cos(x)}$ and how to derive a composition of functions.

Derivatives of elementary functions

Main article: Annex: derivatives

Most derivative calculations require you to eventually take the derivative of some common functions. The following incomplete table provides some of the more frequently used functions of a real variable and their derivatives.

Table of derivatives of some elemental functions
Function $f$		Derivative $f'$
Power function	Constant function ${displaystyle f(x)=k,quad kin mathbf {R} }$	${displaystyle f'(x)=0}$
	Function identity ${displaystyle f(x)=x}$	${displaystyle f'(x)=1}$
	Power of natural exponent: ${displaystyle f(x)=x^{n},quad n=0,1,2,3ldots }$	${displaystyle f'(x)=nx^{n-1}}$
	Square root function ${displaystyle f(x)={sqrt {x}}}$	${displaystyle f'(x)={frac {1}{2{sqrt {x}}}}}$
	Mutual function ${displaystyle f(x)={frac {1}{x}}}$	${displaystyle f'(x)=-{frac {1}{x^{2}}}}$
	General case: ${displaystyle f(x)=x^{r},quad rin mathbf {R} }$	${displaystyle f'(x)=rx^{r-1}}$
Exponential function	Base $e$ : ${displaystyle f(x)=e^{x}}$	${displaystyle f'(x)=e^{x}}$
Exponential function	General case: $0}" xmlns="http://www.w3.org/1998/Math/MathML">f(x)=ax,a한 한 R,a▪0{displaystyle f(x)=a^{x},quad ain mathbf {R}a HCFC}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/5ed11cae27e9934d4fb44218e47c3995e91c2300" style="vertical-align: -0.838ex; width:25.873ex; height:2.843ex;"/>$	${displaystyle f'(x)=a^{x}ln(a)}$
Logarithmic function	Logaritmo on base $e$ : ${displaystyle f(x)=ln x}$	$0}" xmlns="http://www.w3.org/1998/Math/MathML">f♫(x)=1x,x▪0{displaystyle f'(x)={frac {1}{x}}},quad x censo0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1c440a9ae73f74ee87a4d2d19899b16fe497a0c5" style="vertical-align: -1.838ex; width:19.356ex; height:5.176ex;"/>$
Logarithmic function	General case: $0}" xmlns="http://www.w3.org/1998/Math/MathML">f(x)=loga (x),a한 한 R,a▪0{displaystyle f(x)=log _{a}(x),quad ain mathbf {R}a verbal0}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3716cf227411ca60cfa46c85e0ffb3b018e61f84" style="vertical-align: -0.838ex; width:30.684ex; height:2.843ex;"/>$	$0}" xmlns="http://www.w3.org/1998/Math/MathML">f♫(x)=1xln (a),x▪0{displaystyle f'(x)={frac {1}{xln(a)},quad x 20050}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/99dc8ed4441af940dfd4129323730f4f65160747" style="vertical-align: -2.671ex; width:24.721ex; height:6.009ex;"/>$
trigonometric functions	Sinus function: ${displaystyle f(x)=sin(x)}$	${displaystyle f'(x)=cos(x)}$
	Cosine function: ${displaystyle f(x)=cos(x)}$	${displaystyle f'(x)=-sin(x)}$
	Tangent function: ${displaystyle f(x)=tan(x)}$	${displaystyle f'(x)=sec ^{2}(x)={frac {1}{cos ^{2}(x)}}=1+tan ^{2}(x)}$
Reverse trigonometric functions	Archaeal function: ${displaystyle f(x)=arcsin(x)}$	${displaystyle f'(x)={frac {1}{sqrt {1-x^{2}}}}}$
	Archcosene function: ${displaystyle f(x)=arccos(x)}$	${displaystyle f'(x)=-{frac {1}{sqrt {1-x^{2}}}}}$
	Archaegent function: ${displaystyle f(x)=arctan(x)}$	${displaystyle f'(x)={frac {1}{1+x^{2}}}}$

↑ a b As they are written, these derivatives would be defined for any real number $x$ except 0. However, since the logarithm is only defined for values $x$ strictly greater than 0, the domain of its derivatives must also be restricted to positive numbers.

Usual referral rules

Main article: Differentiation rules

In many cases, calculating complicated limits by directly applying Newton's difference quotient can be bypassed by applying differentiation rules. Some of the most basic rules are as follows:

Rule of the constantYes f(x) is constant, then

{displaystyle f'(x)=0.,}

Rule of the amount:

{displaystyle (f+g)'=f'+g'}

for any function f and g and all real numbers $alpha$ and $beta$ .

Product rule:

(fg)'=f'g+fg',

for all functions f and g. By extension, this means that the derivation of a constant multiplied by a function is the constant multiplied by the derivative of the function. For example,

{frac {d}{dr}}pi r^{2}=2pi r.,

quotient rule:

left({frac {f}{g}}right)'={frac {f'g-fg'}{g^{2}}}

for all functions f and g for all such values g 0.

Chain ruleYes $f(x)=h(g(x))$ , being g derivable in x, and h derivable in g(x), then

f'(x)=h'(g(x))cdot g'(x).,

Calculation example

The derivative of

f(x)=x^{4}+sin(x^{2})-ln(x)e^{x}+7,

{begin{aligned}f'(x)&=4x^{(4-1)}+{frac {dleft(x^{2}right)}{dx}}cos(x^{2})-{frac {dleft(ln {x}right)}{dx}}e^{x}-ln {x}{frac {dleft(e^{x}right)}{dx}}+0\&=4x^{3}+2xcos(x^{2})-{frac {1}{x}}e^{x}-ln(x)e^{x}.end{aligned}}

Here, the second term was calculated using the chain rule and the third using the product rule. The known derivatives of elementary functions x², x⁴, sin(x), ln(x) and exp(x) = e^x, as well as the constant 7, were also used.

Differentiability

A domain function in a subset of the reals is differential at a point $x$ if your derivative exists at that point; a function is differentiated at an open interval if it is differentiated at all interval points.

If a function is differential at a point $x$ , the function is continuous at that point. However, a continuous function in $x$ , may not be differential at that point (critical point). In other words, differentiability implies continuity, but not its reciprocal.

The derivative of a differentiable function can be, in turn, differentiable. The derivative of a first derivative is called the second derivative. Similarly, the derivative of a second derivative is the third derivative, and so on. This is also called successive derivation or higher order derivatives.

Generalizations of the concept of derivatives

The simple concept of the derivative of a real function of a single variable has been generalized in several ways:

For functions of several variables:
- Partial derivativewhich applies to actual functions of several variables.
- Directional derivativeextends the concept of partial derivation.
In complex analysis:
- Holomorfa functionwhich extends the concept of derivative to a certain type of functions of complex variables.
In functional analysis:
- Fractional derivativewhich extends the concept of derivatives of order superior to order r, r it does not necessarily need to be an integer as it happens in conventional derivatives.
- Functional derivative, which applies to functional whose arguments are functions of a non finite dimension vector space.
- Derived in the sense of distributions, extends the concept of derivation to generalized functions or distributions, so the derivation of a discontinuous function can be defined as a distribution.
In differential geometry:
- La Referral a concept of differential geometry.
In theory of probability and theory of measure:
- Derived from Malliavin derived from a stochastic or random variable process that changes over time.
- Radon-Nikodym derivative used in measurement theory.

Variability:
- Variance, another possible generalization for functions of several variables when there are continuous derivatives in all directions is that of:
- Differential function, which applies to actual functions of several variables that have partial derivatives according to any of the variables (The argument of a function of several variables belongs to a space of the type $mathbb {R} ^{n}$ dimension n finite).
- La Difference in the sense of Fréchet generalizes the concept of differential function to Banach spaces of infinite dimension.

Applications

Partial derivative, suppose we are on a bridge and observe how the concentration of fish varies with the time exactly. We are in a fixed position of space, so it is a partial derivative of concentration over time keeping the position fixed in the direction "x", "y" or "z".

Total derivative over time, suppose we move in a motorboat that moves in the river in all directions, sometimes against the current, others through and others in favor. In referring the variation of concentration of fish over time, the numbers that result must also reflect the movement of the boat. The variation of concentration with time corresponds to the total derivative.

Substantial derivative over time, suppose we go in a canoe that does not communicate energy, but simply floats. In this case, the speed of the observer is exactly the same as the speed of the current "v". When referring to the variation in the concentration of fish over time, the numbers depend on the local speed of the current. This derivative is a special class of total derivative with respect to the time that is referred to as the substantial derivative, or sometimes (more logically) derived following the movement.

Contenido relacionado

Más resultados...