Density
In physics and chemistry, density (from Latin, densĭtas, -ātis) is a scalar quantity referring to the amount of mass in a given volume of a substance or a solid object. It is usually symbolized by the letter rho (ρ) of the Greek alphabet.
History
According to a popular story, Archimedes was commissioned to determine whether the goldsmith of Hiero II of Syracuse had embezzled gold during the manufacture of a crown dedicated to the gods, substituting it for another, cheaper metal (a process known as alloying). Archimedes knew that the irregularly shaped crown could be crushed or cast into a cube whose volume could be easily calculated compared to the mass. But the king did not agree with this method, as it would have meant the destruction of the crown.
Archimedes took a relaxing plunge bath, and watching the hot water rise as he stepped into it, he discovered that he could calculate the volume of the gold crown by the displacement of the water. Once the volume was found, it could be multiplied by the density of gold, finding the weight it should have if it were pure gold (the density of gold is very high, 19,300 kg/m³, and any other metal alloyed with it has a lower density).), then if the weight was not the one that would correspond if it were made of gold, it would mean that the crown would have an alloy of another metal.
Supposedly, making this discovery, he ran naked through the streets shouting, "Eureka! Eureka!» (Εύρηκα! in Greek, which means: 'I found it!'). As a result, the term "eureka" entered common parlance, and is used today to indicate a moment of enlightenment.
The story first appeared in written form in De Architectura, by Marcus Vitruvius, two centuries after it supposedly took place. However, some scholars have doubted the veracity of this account, arguing (among other things) that the method would have required exact measurements that would have been difficult to make at the time.
Another version of the story says that Archimedes noticed that he was experiencing an upward push when submerged in water, and thought that by weighing the crown, submerged in water, and on the other pan of the scales putting the same weight in gold, also submerged, the scales would be balanced if the crown was indeed gold. Certainly the upward push of the water would be the same if objects of the same volume and the same weight were in the two saucers. With this, the difficulty of knowing exactly the volume of the irregularly shaped solid, at the time, was put aside. From this other version the idea of Archimedes' principle was born.
Much later, the concept of density was born among scientists, at a time when the units of measurement were different in each country. To avoid expressing it in terms of the various units of measurement usual for each one, and not having to make the necessary conversions, physicists assigned to each matter a dimensionless number, which was the ratio between the mass of that matter and that of a equal volume of pure water, a substance found in any laboratory (relative density). When the unit of weight was fixed in the metric system, the kilogram, as one cubic decimeter (one liter) of pure water, the figure used until then, coincided with the absolute density (if measured in kilograms per liter, a unit of volume in the old decimal metric system, although accepted by the SI, and not in kilograms per cubic meter, which is the SI unit of volume).
Types of density
Absolute density
Absolute density is the magnitude that expresses the relation between the mass and the volume of a substance or a solid object. Its unit in the International System is kilogram per cubic meter (kg/m³), although it is frequently also expressed in g/cm³. Density is an intensive quantity.
- ρ ρ =mV{displaystyle rho ={frac {m}{V}}}}
| Symbol | Name |
|---|---|
| ρ ρ {displaystyle rho } | weight |
| m{displaystyle m} | Masa |
| V{displaystyle V} | Volume of substance |
Relative density
The relative density of a substance is the relationship between its density and that of another reference substance; consequently, it is a dimensionless magnitude (without units)
| Symbol | Name |
|---|---|
| ρ ρ r{displaystyle rho _{r}} | Relative density |
| ρ ρ {displaystyle rho } | Density of the substance |
| ρ ρ 0{displaystyle rho _{0}} | Reference density or absolute |
For liquids and solids, the usual reference density is that of liquid water at a pressure of 1 atm and a temperature of 4 °C. Under these conditions, the absolute density of distilled water is 1000 kg/m³, that is, 1 kg/dm³.
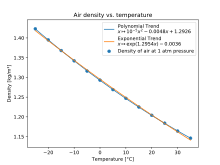
For gases, the usual reference density is that of air at a pressure of 1 atm and a temperature of 0 °C.
Average density and point density
For a homogeneous system, the mass/volume expression can be applied in any region of the system always obtaining the same result.
However, a heterogeneous system does not have the same density in different parts. In this case, you have to measure the "average density", dividing the mass of the object by its volume or the "point density" which will be different at each point, position or "infinitesimal" of the system, and that will be defined by:
ρ ρ =limV→ → 0mV=dmdV{displaystyle rho =lim _{Vto 0}{frac {m}{V}}={frac {dm}{dm}{dV}}}}}}}}}}
However, it should be noted that the continuum mechanics assumptions are only valid up to scales of 10-8 m, since that at atomic scales density is not well defined. For example, the size of the atomic nucleus is approximately 10-13 m and the vast majority of the atomic mass is concentrated in it, therefore that its density (2.3·1017 kg/m³) is much higher than that of ordinary matter. That is, at the atomic scale the density is far from uniform, since the atoms are essentially empty, with practically all the mass concentrated in the atomic nucleus.
Bulk density
The apparent density is a magnitude applied to materials of heterogeneous constitution, and among them, the porous ones such as the soil, which form heterogeneous bodies with interstices of air or another substance, so that the total density of a volume of the material is less than the density of the porous material if it were compacted. In the case of a material mixed with air we have:
ρ ρ ap=mapVap=mr+maireVr+Vaire{displaystyle rho _{ap}={frac {m_{ap}}}{V_{ap}}}}}}}{{{frac {m_{r}+m_{aire}}{V_{r}}}
The apparent density of a material is not an intrinsic property of the material and depends on its compaction. Apparent soil density (ρ ρ ap{displaystyle rho _{ap}}) is obtained by secating a soil sample of a volume known at 105 °C to constant weight.
| Symbol | Name |
|---|---|
| ρ ρ ap{displaystyle rho _{ap}} | Apparent soil density |
| WSS{displaystyle W_{SS}} | Dry soil weight at 105 °C to constant weight |
| VS{displaystyle V_{S}} | Original volume of the soil sample |
It should be considered that for soil samples that vary their volume at the time of drying, such as soils with a high concentration of 2:1 clays, the water content that the sample had at the time of taking the volume should be expressed.
In construction, the apparent density of work elements is considered, such as a brick wall, which contains bricks, cement or plaster mortar and air voids (when the brick is hollow or perforated).
Density changes
In general, the density of a substance varies when pressure or temperature changes, and in changes of state. In particular, it has been established empirically:
- When pressure increases, the density of any stable material also increases, notably in gases, almost inaccurately in liquids and solids.
- As a general rule, by increasing temperature, density decreases (if the pressure remains constant). However, there are notable exceptions to this rule. For example, freshwater density grows between the melting point (to 0 °C) and 4 °C; something similar occurs with silicon at low temperatures.[chuckles]required]
- Practically and depending on the type of problem that is being solved, fluids and solids can be considered constant density. This is because the variations in dilating or contracting due to pressure and/or temperature changes are relatively small.
The effect of temperature and pressure on solids and liquids is very small, so typically the compressibility of a liquid or solid is 10−6 bar−1 (1 bar=0.1 MPa) and the coefficient of thermal expansion is of the order of 10−5 K−1 The above considerations lead to a equation of state for an ordinary substance must satisfy the following restrictions:
(♪)φ φ (ρ ρ ,p,T)=0,{▪ ▪ ρ ρ ▪ ▪ T=− − ▪ ▪ φ φ ▪ ▪ T(▪ ▪ φ φ ▪ ▪ ρ ρ )− − 1≤ ≤ 0▪ ▪ ρ ρ ▪ ▪ p=− − ▪ ▪ φ φ ▪ ▪ p(▪ ▪ φ φ ▪ ▪ ρ ρ )− − 1≥ ≥ 0{cHFFFFFF}{cH00FF00}{cH00FFFF00}{cH00FF00}{cH00FF00}{cH00FFFF00}{cH00FFFF00}{cH00FFFF00}{cH00FF00}{cH00FFFF00}{cH00FFFFFF00}{cH00}{cH00}{cH00FFFFFFFFFF00}{cH00}{cH00FFFFFFFFFFFFFF00}{cH00}{cH00}{cH00}{cH00}{cH00FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF00}{cH00}{cH00}{cH00}{cH00}{cH00}{cH00FFFFFF00}{cH00}{cH00FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFF
On the other hand, the density of gases is greatly affected by pressure and temperature. The ideal gas law mathematically describes the relationship between these three quantities:
(**)ρ ρ =pMRT{displaystyle rho ={frac {p,M}{R,T}}}}
where R{displaystyle R,} is the universal constant of ideal gases, p{displaystyle p,} It's gas pressure, M{displaystyle M,} their molar mass and T{displaystyle T,} absolute temperature. That means an ideal gas to 300 K (27 °C) and 1 atm will double its density if the pressure is increased to 2 atm maintaining the temperature constant or, alternatively, its temperature is reduced to 150 K while maintaining constant pressure. As relationships can be checked () are also satisfied in ()
Measurement
Density can be obtained indirectly and directly. For the indirect determination of the density, the mass and volume are measured separately and the density is subsequently calculated. Mass is usually measured with a balance, while volume can be measured by determining the shape of the object and measuring the appropriate dimensions, or by displacement of a liquid, among other methods. The most common instruments for measuring density are:
- The densmeter, which allows the direct measurement of the density of a liquid.
- The picnometer, which allows the precise measurement of the density of solids, liquids and gases (gas cylinder).
- The hydrostatic balance, which allows to calculate solid density.
- The balance of Mohr (hydrostatic scale variable), which allows precise measurement of fluid density.
Another possibility to determine the densities of liquids and gases is to use a digital instrument based on the principle of the oscillating U-tube. Whose resonant frequency is determined by the materials contained, as the mass of the tuning fork is decisive for the height of the sound
Units
The most commonly used units of measurement are:
In the International System of Units (SI):
- kilogram per cubic meter (kg/m3).
Other units to express density are:
- grams per cubic centimeter (g/cm3).
- kilogram per litre (kg/L) or kilogram per cubic decimeter. Water density is approximately 1 kg/L (1000 g/dm3 = 1 g/cm3 = 1 g/mL).
- gram per milliliter (g/mL), which is equivalent to (g/cm3).
- For the gases the gram by cubic decimeter (g/dm3) or gram per litre (g/L), in order to simplify with the universal constant of ideal gases:
- R=0,082atm⋅ ⋅ Lmol⋅ ⋅ K{displaystyle R=0,082 {frac {{text{atm}}{cdot {text{L}}{{{{{{text{mol}}}}}{cdot {text{K}}}}}}}}}}{{{{cdot {c {text{text{text{text{text{c}}}}}}}}}}}}}}}}}}}}}}}
In the Anglo-Saxon system of units:
- ounce per cubic inch (oz/in3)
- pound per cubic inch (lb/in3)
- pound per cubic foot (lb/ft3)
- pound per cubic yard (lb/yd3)
- pound per gallon (lb/gal)
- pound by American bushel (lb/bu)
- slug.
Density of chemical elements
Density of chemical elements under laboratory conditions, expressed in g cm−3 (elements with a density greater than that of osmium or iridium only have a theoretical densityː radioactive elements super -heavy are produced in too low amounts or decay too rapidly to allow measurement):
| H 0.0709 | He 0.126 | ||||||||||||||||
| Li 0.534 | Be 1.848 | B 2.34 | C 2 | N 0.81 | O 1.14 | F 1,505 | Ne 1.2 | ||||||||||
| Na 0.971 | Mg 1.738 | Al 2.6989 | Yeah. 2.33 | P 1,82 | S 2.07 | Cl 1.56 | Ar 1.4 | ||||||||||
| K 0.89 | Ca 1.54 | Sc 2.989 | Ti 4.51 | V 6 | Cr 7.15 | Mn 7.3 | Fe 7.874 | Co 8.9 | Ni 8,902 | Cu 8.96 | Zn 7,134 | Ga 5,904 | Ge 5,323 | As 5,72 | Separate 4.79 | Br 3.12 | Kr 2.6 |
| Rb 1,532 | Mr. 2.64 | And 4,469 | Zr 6.52 | Nb 8,57 | Mo 10,22 | Tc 11,5 | Ru 12.1 | Rh 12,41 | Pd 12,02 | Ag 10.5 | Cd 8,69 | In 7.31 | Sn 7.29 | Sb 6.68 | You 6.23 | I 4.93 | Xe 3,06 |
| Cs 1.87 | Ba 3.62 | ♪ | Hf 13,31 | Ta 16.4 | W 19.3 | Re 20.8 | You 22.587 | Go 22,562 | Pt 21.45 | Au 19.3 | Hg 13,546 | Tl 11.85 | Pb 11,35 | Bi 9,797 | Po 9,2 | At | Rn |
| Fr 1.87 | Ra 5 | ** | Rf 23.2 | Db 29.3 | Sg 35 | Bh 37.1 | Hs 40.7 | Mt 37.4 | Ds 34.8 | Rg 28.7 | Cn | Nh | Fl | Mc | Lv | Ts | Og |
| ♪ | La 6,145 | Ce 6.77 | Pr 6.773 | Nd 7,008 | Pm 7,264 | Sm 7.52 | Eu 5.244 | Gd 7,901 | Tb 8,23 | Dy 8,551 | Ho 8.795 | Er 9,066 | Tm 9,321 | Yb 6.9 | Lu 9,841 | ||
| ** | Ac 10 | Th 11.72 | Pa 15,37 | U 19.1 | Np 20,25 | Pu 19.816 | Am 12 | Cm 13,51 | Bk 13,25 | Cf 15.1 | That's it. 8,84 | Fm 1.69 | Md | No. 11.4 | Lr 81 | ||
Density of the elements at their melting point in g cm−3ː
| H 0.071 | He | ||||||||||||||||
| Li 0,512 | Be 1.69 | B 2.08 | C 2.26 | N | O | F | Ne | ||||||||||
| Na 0.927 | Mg 1,584 | Al 2,375 | Yeah. 2.57 | P | S 1.819 | Cl | Ar 1.4 | ||||||||||
| K 0.828 | Ca 1.378 | Sc 2.8 | Ti 4,11 | V 5.5 | Cr 6.3 | Mn 5,95 | Fe 6.98 | Co 7.75 | Ni 7.81 | Cu 8,02 | Zn 6.57 | Ga 6.08 | Ge 5.6 | As 5,22 | Separate 3,99 | Br | Kr |
| Rb 1.46 | Mr. 6.98 | And 4.24 | Zr 5.6 | Nb | Mo 9,33 | Tc | Ru 10,65 | Rh 10.7 | Pd 10,38 | Ag 9,32 | Cd 7.996 | In 7.02 | Sn 6.99 | Sb 6.53 | You 5.7 | I | Xe |
| Cs 1,843 | Ba 3,338 | ♪ | Hf | Ta 15 | W 17.6 | Re 18.9 | You 20 | Go 19 | Pt 19,77 | Au 17,31 | Hg | Tl 11,22 | Pb 10,66 | Bi 10,05 | Po | At | Rn |
| Fr | Ra | ** | Rf | Db | Sg | Bh | Hs | Mt | Ds | Rg | Cn | Nh | Fl | Mc | Lv | Ts | Og |
| ♪ | La 5,94 | Ce 6.55 | Pr 6.5 | Nd 6.89 | Pm | Sm 7.16 | Eu 5.13 | Gd 7.4 | Tb 7.65 | Dy 8,37 | Ho 8,34 | Er 8,86 | Tm 8,56 | Yb 6.21 | Lu 9,3 | ||
| ** | Ac | Th | Pa | U 17,3 | Np | Pu 16,63 | Am 11.7 | Cm | Bk 18.5 | Cf | That's it. | Fm | Md | No. | Lr | ||
Contenido relacionado
Theory of color
Infinitesimal
André-Marie Ampere