Crystalline system
A crystalline solid is built from the repetition in space of an elementary parallelepiped structure called a unit cell. The seven crystal systems are triclinic, monoclinic, orthorhombic, tetragonal, trigonal, hexagonal, and cubic. Informally, two crystals are in the same crystal system if they have similar symmetries (although there are many exceptions).
Depending on the lattice parameters, that is, the lengths of the sides or axes of the elementary parallelepiped and the angles they form, seven crystalline systems can be distinguished:
| Crystal system | Axis | Angles between axes |
|---|---|---|
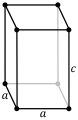
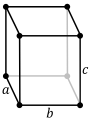
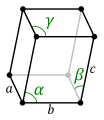
| Cube | a = b = c | α = β = γ = 90° |
| Tetragonal | a = bloc | α = β = γ = 90° |
| Orthrombic (or Rhombic) | a. | α = β = γ = 90° |
| Hexagonal | a = bloc | α = β = 90°; γ = 120° |
| Trigonal (or Romboédrico) | a = b = c | α = β = γ, 90° |
| Monoclinic | a. | α = γ = 90°; βIE 90° |
| Triclinic | a. | α α β γ
α, β, γ ì 90° |
Based on the possible locations of the atoms in the unit cell, 14 basic crystalline structures are established, the so-called Bravais lattices.
Classifications
Crystals can be classified in other ways, including crystal families and lattice systems. These use space group, networks and point group. The various classifications are often confused: in particular, the trigonal crystal system is often confused with the rhombohedral lattice system, and the term "crystal system" is sometimes used to refer to one of the others.
Space with fewer than three dimensions have the same number of crystal systems, crystal families, and lattice systems. In a one-dimensional space, there is a system of crystals. In 2D space, there are four crystal systems: oblique, rectangular, square, and hexagonal.
Crystal family
A family of crystals is determined by the lattices and the groups of points. It is formed by combining crystal systems that have space groups assigned to a common lattice system. In three dimensions, crystal families and systems are identical, except for hexagonal and trigonal crystal systems, which are combined into a hexagonal crystal family. The six families of crystals are triclinic, monoclinic, orthorhombic, tetragonal, hexagonal, and cubic.
Crystal lattice system
A crystal lattice system is a group of crystal lattices with the same set of point groups, which are subgroups of the arithmetic classes of crystals. Space groups and crystals are classified as lattice systems based on their Bravais lattices. The 14 Bravais lattices are grouped into seven latticing systems: triclinic, monoclinic, orthorhombic, tetragonal, rhombohedral, hexagonal, and cubic.
Five of the crystal systems are essentially the same as five of the lattice systems, while the hexagonal and trigonal crystal systems are different.
Most point groups are assigned to a single grid system, in which case both the crystal and the grid system have the same name. However, five groups of points are assigned to two lattice systems, the rhombohedral and the hexagonal, because both present triple rotational symmetry. These point groups are assigned to the trigonal crystal system.
The relationship between three-dimensional crystal families, crystal systems and lattice systems is shown in the following table:
| Crystal family | Crystal system | Required symmetries of the group of points | Points groups | Space group | Bravais Networks | Network system |
|---|---|---|---|---|---|---|
| Triclinic | Triclinic | None | 2 | 2 | 1 | Triclinic |
| Monoclinic | Monoclinic | 1 double shaft rotation or 1 mirror plane | 3 | 13 | 2 | Monoclinic |
| Orthodox | Orthodox | 3 double rotation axles or 1 double rotation axle and 2 mirror planes | 3 | 59 | 4 | Orthodox |
| Tetragonal crystal system | Tetragonal | 1 quadruple rotation axis | 7 | 68 | 2 | Tetragonal |
| Hexagonal | Trigonal | 1 triple rotation axle | 5 | 7 | 1 | Romboedro |
| 18 | 1 | Hexagonal | ||||
| Hexagonal | 1 sextuple rotation axis | 7 | 27 | |||
| Cube | Cube | 4 triple rotation axles | 5 | 36 | 3 | Cube |
| 6 | 7 | Total | 32 | 230 | 14 | 7 |
- Note: There is no "trigonal" network system. In order to avoid the confusion of terminology, the term "gallory" is not used.
Elements of symmetry
The type of normal crystalline system depends on the symmetrical and repetitive arrangement of the faces that make up the crystal. This arrangement is a consequence of the internal ordering of its atoms and, therefore, characteristic of each mineral. The faces will be arranged according to the symmetry elements that this system has, one of them being characteristic of each of the seven systems:
| Crystal system | Characteristic elements |
|---|---|
| Cube | Four alternative axes |
| Tetragonal | A quaternary axis (or derivative binary) |
| Orthodox | Three binary axes or three symmetry planes |
| Hexagonal | A senary axis (or derivative ternary) |
| Trigonal (or Romboédrica) | A tender axis |
| Monoclinic | A binary axis or a plane of symmetry |
| Triclinic | A symmetry center or no symmetry |
Types
In other dimensions
Two-dimensional space
Two-dimensional space has the same number of crystal systems, crystal families, and lattice systems. In 2D space, there are four crystal systems: oblique, rectangular, square, and hexagonal.
Four-dimensional space
The four-dimensional unit cell is defined by four edge lengths (a, b, c, d) a and six interaxial angles (α, β, γ, δ, ε, ζ). The following conditions for lattice parameters define 23 families of crystals
| N.o | Family | Longitudes of edge | Interaxial angles |
|---|---|---|---|
| 1 | Hexaclin | a I was. b I was. c I was. d | α I was. β I was. γ I was. δ I was. ε I was. γ 90° |
| 2 | Triclinic | a I was. b I was. c I was. d | α I was. β I was. γ 90° δ = ε = γ = 90° |
| 3 | Diclinic | a I was. b I was. c I was. d | α 90° β = γ = δ = ε = 90° γ 90° |
| 4 | Monoclinic | a I was. b I was. c I was. d | α 90° β = γ = δ = ε = γ = 90° |
| 5 | Ortogonal | a I was. b I was. c I was. d | α = β = γ = δ = ε = γ = 90° |
| 6 | Tetragonal monoclinic | a I was. b = c I was. d | α 90° β = γ = δ = ε = γ = 90° |
| 7 | Hexagonal monoclinic | a I was. b = c I was. d | α 90° β = γ = δ = ε = 90° γ = 120° |
| 8 | Ditetragonal diclinic | a = d I was. b = c | α = γ = 90° β = ε 90° γ 90° δ = 180° − γ |
| 9 | Ditrigonal diclinic (dihexagonal) | a = d I was. b = c | α = γ = 120° β = ε 90° γ I was. δ 90° # δ ♪ β − γ |
| 10 | Ortogonal tetragonal | a I was. b = c I was. d | α = β = γ = δ = ε = γ = 90° |
| 11 | Ortogonal hexagonal | a I was. b = c I was. d | α = β = γ = δ = ε = 90°, γ = 120° |
| 12 | Ditetragonal monoclinic | a = d I was. b = c | α = γ = δ = γ = 90° β = ε 90° |
| 13 | Ditrigonal (dihexagonal) monoclinic | a = d I was. b = c | α = γ = 120° β = ε 90° γ = δ 90° # γ = −1/2# β |
| 14 | Ditetragonal ortogonal | a = d I was. b = c | α = β = γ = δ = ε = γ = 90° |
| 15 | Tetragonal hexagonal | a = d I was. b = c | α = β = γ = δ = ε = 90° γ = 120° |
| 16 | Dihexagonal ortogonal | a = d I was. b = c | α = γ = 120° β = γ = δ = ε = 90° |
| 17 | Orthogonal cubic | a = b = c I was. d | α = β = γ = δ = ε = γ = 90° |
| 18 | 8th | a = b = c = d | α = γ = γ 90° β = ε = 90° δ = 180° − α |
| 19 | Decagonal | a = b = c = d | α = γ = γ I was. β = δ = ε # β = −1/2 − α |
| 20 | Dodecagonal | a = b = c = d | α = γ = 90° β = ε = 120° γ = δ 90° |
| 21 | Diisohexagonal ortogonal | a = b = c = d | α = γ = 120° β = γ = δ = ε = 90° |
| 22 | Icosagonal (icosaedro) | a = b = c = d | α = β = γ = δ = ε = γ # α = −1/4 |
| 23 | Hypercubic | a = b = c = d | α = β = γ = δ = ε = γ = 90° |
Names here are given according to Whittaker. They are almost the same as in Brown et al, with the exception of the names of crystal families 9, 13 and 22. The names of these three families according to Brown et al are given in parentheses.
The relationship between families of four-dimensional crystals, crystal systems, and lattice systems is shown in the following table. Enantiomorphic systems are marked with an asterisk. The number of enantiomorphic pairs is given in parentheses. Here, the term "enantiomorphic" has a different meaning than the table for three-dimensional crystal classes. The latter means that enantiomorphic point groups describe chiral (enantiomorphic) structures. In the current table, "enantiomorphic" means that a group itself (considered as a geometric object) is enantiomorphic, such as enantiomorphic pairs of three-dimensional space groups P31 and P32, P4122 and P4322. From four-dimensional space, point groups can also be enantiomorphic in this sense.
| No. Crystal family | Crystal family | Crystal system | N.o. crystal system | Points groups | Space groups | Bravais Networks | Jealousy system |
|---|---|---|---|---|---|---|---|
| I | Hexaclin | 1 | 2 | 2 | 1 | P hexaclinic | |
| II | Triclinic | 2 | 3 | 13 | 2 | P, S triclinical | |
| III | Diclinic | 3 | 2 | 12 | 3 | P, S, D diclinic | |
| IV | Monoclinic | 4 | 4 | 207 | 6 | P, S, S, I, D, F monoclinic | |
| V | Ortogonal | Ortogonal no axial | 5 | 2 | 2 | 1 | Ortogonal KU |
| 112 | 8 | Ortogonal P, S, I, Z, D, F, G, U | |||||
| Ortogonal axial | 6 | 3 | 887 | ||||
| VI | Tetragonal monoclinic | 7 | 7 | 88 | 2 | P monoclinic tetragonal, I | |
| VII | Hexagonal monoclinic | Monoclinic Trigonal | 8 | 5 | 9 | 1 | Hexagonal monoclinic R |
| 15 | 1 | Hexagonal monoclinic P | |||||
| Hexagonal monoclinic | 9 | 7 | 25 | ||||
| VIII | Ditetragonal diclinic* | 10 | 1 (+1) | 1 (+1) | 1 (+1) | Ditetragonal diclinic P* | |
| IX | Ditetragonal diclinic* | 11 | 2 (+2) | 2 (+2) | 1 (+1) | Ditrigonal diclinic P* | |
| X | Ortogonal tetragonal | Inverse tetragonal orthogonal | 12 | 5 | 7 | 1 | Ortogonal tetragonal KG |
| 351 | 5 | Ortogonal tetragonal P, S, I, Z, G | |||||
| Ortogonal tetragonal own | 13 | 10 | 1312 | ||||
| XI | Ortogonal hexagonal | Ortogonal trigonal | 14 | 10 | 81 | 2 | Ortogonal hexagonal R, RS |
| 150 | 2 | Ortogonal hexagonal P, S | |||||
| Ortogonal hexagonal | 15 | 12 | 240 | ||||
| XII | Ditetragonal monoclinic* | 16 | 1 (+1) | 6 (+6) | 3 (+3) | Ditetragonal monoclinic P*, S*, D* | |
| XIII | Ditrigonal monoclinic* | 17 | 2 (+2) | 5 (+5) | 2 (+2) | Ditrigonal monoclinic P*, RR* | |
| XIV | Ditetragonal ortogonal | Cripto-ditetragonal ortogonal | 18 | 5 | 10 | 1 | Ditetragonal ortogonal D |
| 165 (+2) | 2 | Ditetragonal ortogonal P, Z | |||||
| Ditetragonal ortogonal | 19 | 6 | 127 | ||||
| XV | Hexagonal tetragonal | 20 | 22 | 108 | 1 | Hexagonal tetragonal P | |
| XVI | Dihexagonal ortogonal | Cripto-ditrigonal ortogonal* | 21 | 4 (+4) | 5 (+5) | 1 (+1) | Dihexagonal ortogonal G* |
| 5 (+5) | 1 | Dihexagonal ortogonal P | |||||
| Dihexagonal ortogonal | 23 | 11 | 20 | ||||
| ditrigonal ortogonal | 22 | 11 | 41 | ||||
| 16 | 1 | Dihexagonal ortogonal RR | |||||
| XVII | Cubic Orthogonal | Simple cubical orthogonal | 24 | 5 | 9 | 1 | Cubic Orthogonal KU |
| 96 | 5 | Ortogonal cubic P, I, Z, F, U | |||||
| Ortogonal cubic complex | 25 | 11 | 366 | ||||
| XVIII | Eighth* | 26 | 2 (+2) | 3 (+3) | 1 (+1) | 8th P* | |
| XIX | Decagonal | 27 | 4 | 5 | 1 | Dec. P | |
| XX. | Dodecagonal* | 28 | 2 (+2) | 2 (+2) | 1 (+1) | Dodecagonal P* | |
| XXI | Ortogonal diisohexagonal | Ortogonal diisohexagonal simple | 29 | 9 (+2) | 19 (+5) | 1 | Ortogonal diisohexagonal RR |
| 19 (+3) | 1 | Ortogonal diisohexagonal P | |||||
| Ortogonal diisohexagonal complex | 30 | 13 (+8) | 15 (+9) | ||||
| XXII | Icosagonal | 31 | 7 | 20 | 2 | Icosagonal P, SN | |
| XXIII | Hypercubic | Octagonalc | 32 | 21 (+8) | 73 (+15) | 1 | P |
| 107 (+28) | 1 | Hypercube Z | |||||
| Dodecagonal hypercobic | 33 | 16 (+12) | 25 (+20) | ||||
| Total | 23 (+6) | 33 (+7) | 227 (+44) | 4783 (+111) | 64 (+10) | 33 (+7) | |
Contenido relacionado
Absolute zero
Azimuth
James Prescott Joule