Coordinate system

ImprimirCitar

Three-dimensional Cartesian coordinate system

In geometry, a coordinate system is a reference system that uses one or more numbers (coordinates) to univocally determine the position of a point or geometric object. The order in which the coordinates are written is significant, and they are sometimes identified by their position in an ordered tuple; they can also be represented by letters, such as “the x-coordinate”. The study of coordinate systems is the object of analytical geometry, which allows to formulate geometric problems in a "numerical" way.

In geometry, coordinates are quantities that determine the position of a point on a plane or in space. In a plane, the position of a point is usually determined by the distances to two straight lines (coordinate axes) that intersect at a point (origin) at right angles; One of the coordinates is called the ordinate and the other is called the abscissa. In space according to Descartes' system, the position of a point is determined by the distances to three coordinate planes that intersect at a point at right angles to each other, although other systems are also used, such as spherical coordinates (where the origin is at the center of a series of spheres), or the cylindrical coordinates.

In geography, coordinates are chosen as a roughly spherical coordinate system: latitude, longitude, and height above a known general level (such as the ocean).

In astronomy, celestial coordinates are an ordered pair of angular quantities (for example, right ascension and declination), with which the position of various light points and auxiliary points on the celestial sphere is determined. In practice, various celestial coordinate systems are used. Each of them is essentially a spherical coordinate system (no radial coordinates) with an appropriately chosen fundamental plane and origin. Depending on the choice of the fundamental plane, the celestial coordinate system is called horizontal (horizon plane), equatorial (equatorial plane), ecliptic (ecliptic plane), or galactic (galactic plane).

The most commonly used coordinate system is the rectangular coordinate system, also known as the Cartesian coordinate system.

Coordinates in the plane and in space can be defined in an unlimited number of different ways. The resolution of numerous mathematical or physical problems implies choosing that specific coordinate system in which the problem is solved easier or more convenient in each particular case. A well-known generalization of the coordinate system is reference systems.

Examples of Coordinate Systems

Linear coordinate system

Main article: Actual claim

It is the set of real numbers represented graphically by a line in which all natural numbers, integers, fractions, decimals, etc. can be located.

Each point of the line represents a real number, either through a bi-unique correspondence or through a bi-yective application, used to represent the numbers as specially marked points, such as for example integers by a straight line called straight graduated as the wholeof points sorted and separated from each other at the same distance. The point that represents the zero ( ${displaystyle 0}$ ) is the main reference point of the coordinate system, called the point of origin.

Taking into account that each of the points in the line graphically represents a real number, to the right of the point of origin $O$ are all positive real numbers and to the left all negative real numbers.

To represent a number on the real line, capital letters and their corresponding coordinates are used, for example, the points A(5), B(3), C(-3), D(-5) etc

Cartesian Coordinate System

Main article: Cartesian coordinates

Cartesian coordinates on the plane

In an euclinary space, a cartesian coordinate system is defined by two or three equally scaled orthogonal axes, depending on whether it is a two-dimensional or three-dimensional system (approximately in $scriptstyle mathbb{R} ^{n}$ systems can be defined n- dimensional). The value of each of the coordinates of a point (A) is equal to the orthogonal projection of the position vector of that point ( ${mathbf r}_{{text{A}}}={text{OA}},$ ) on a certain axis:

${mathbf r}_{{text{A}}}={text{OA}}=(x_{{text{A}}},y_{{text{A}}},z_{{text{A}}})$

Each of the axes is defined by a director vector and by the origin of coordinates. For example, the axis x is defined by the origin of coordinates (O) and a vector ( ${mathbf {i}},$ ) such that:

{mathbf {i}}=(1,0,0)

, whose module is

|{mathbf {i}}|=1,

The value of the x coordinate of a point is equal to the orthogonal projection of the position vector of said point on the x axis:

$x_{{text{A}}}={{text{OA}}cdot {mathbf {i}} over |{text{OA}}|cdot |{mathbf {i}}|}={{text{OA}} over |{text{OA}}|}cdot {mathbf {i}}$

Polar Coordinate System

Main article: Polar coordinates

Location of a point in polar coordinates

Polar coordinates are a two-dimensional coordinate system in which each point or position on the plane is determined by an angle and a distance.

Choose a point as pole and it takes a secret from this point as Polar shaft. For a given angle $theta$ , there is a single straight line passing through the pole whose angle with the polar axis is $theta$ (measured in the opposite direction of the clock needles from the axis to the line). Then there is a single point in this line whose distance with sign to origin is r for a given number r. For a couple of coordinates given ${displaystyle (r,theta)}$ There is only one point, but any point is represented by many pairs of coordinates. For example, ${displaystyle (r,theta)}$ , ${displaystyle (r,theta +2pi)}$ and ${displaystyle (-r,theta +pi)}$ are all polar coordinates for the same point. The pole is represented by ${displaystyle (0,theta)}$ for any value of $theta$ .

Log-Polar Coordinate System

Main article: Log-polar coordinates

It is a coordinate system where a point is identified by two numbers, one for the logarithm of the distance to a certain point and another for an angle. Logarithmic coordinates are closely connected to polar coordinates, which are generally used to describe domains in the plane with some kind of rotational symmetry.

Cylindrical Coordinate System

Main article: Cylindrical coordinates

Cylindrical coordinate system

Meaning of cylindrical coordinates

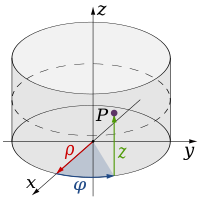
The cylindrical coordinate system $0, 0leq varphi C={(ρ ρ ,φ φ ,z)日本語ρ ρ ▪0,0\leq \leq φ φ .2π π ,z한 한 R!{textstyle {mathcal {C}}={(rhovarphiz) expedient rho δ0, 0leq varphi \leq2pi zin mathbb {R} } 0, 0leq varphi$ is used to represent the points of a three-dimensional euclide space. It is particularly useful in problems with axial symmetry. This coordinate system is a generalization of the system of polar coordinates of the Euclide plane, to which a third orthogonal reference axis is added to the other two. The first coordinate is the distance between the axis ${displaystyle Oz}$ and the point, the second is the angle that forms the axis ${displaystyle Ox}$ and the straight that passes through both points, while the third is the coordinate ${displaystyle z}$ which determines the height of the cylinder.

Spherical Coordinate System

Main article: Spherical coordinates

Spherical coordinates

Geographical coordinates

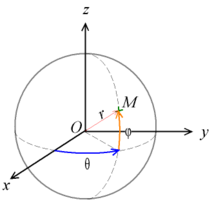
Like cylindrical coordinates, the spherical coordinate system is used in three-dimensional Euclidean spaces. This spherical coordinate system is formed by three mutually orthogonal axes that intersect at the origin. The first coordinate is the distance between the origin and the point, the other two being the angles that need to be rotated to reach the position of the point.

Geographic coordinates

Main article: Geographical coordinates

This type of cartographic coordinates, a subtype of spherical coordinates, is used to define points on a spherical surface. There are several types of geographic coordinates. The most classic and well-known system is the one that uses latitude and longitude, which can be displayed in the following formats:

DD — Decimal Degree (Polar grades): e.g. 49.500-123.500
DM — Degree:Minute (Grades:Minutos): e.g. 49:30.0-123:30.0
DMS — Degree:Minute:Second (Grades:Minutos:Segundes): e.g. 49:30-123:30

You can also define the coordinates of a point on the Earth's surface using a map projection. The most common projected cartographic coordinate system is the UTM coordinate system.

General curvilinear coordinates

Main article: Curviline coordinates

A system of quarrel coordinates is the most general form of parameterizing or labeling the points of a locally eucliding space or a differentiable variety (globally, space can be eucliding, but not necessarily). If it is a locally eucliding space ${displaystyle M}$ dimension ${displaystyle m}$ , you can build a local curvy coordinate system around a point $p$ always from any diphenomorphism that fulfills:

{displaystyle phi:Mto mathbb {R} ^{m}qquad pin Mland phi (p)=(0,0,ldots0)in mathbb {R} ^{m}}

For any point q close to p its curvilinear coordinates are defined as:

{displaystyle phi (q)=(x_{1},x_{2},ldotsx_{m}),}

If locally euclided space has the Riemann variety structure, certain curviline coordinate systems can be classified as orthogonal coordinate systems or even as orthonormal coordinate systems. Cylindrical coordinates and spherical coordinates are particular cases of orthogonal coordinate systems on euclid space $mathbb{R} ^{3}$ .

Orthogonal Curvilinear Coordinates

Main article: Orthogonal coordinates

A curvilinear coordinate system is called orthogonal when the metric tensor expressed in those coordinates has a diagonal form. When this happens, many of the formulas of the differential vector calculus can be written in a particularly simple way in these coordinates, being able to take advantage of this fact when there is, for example, axial, spherical or other symmetry that can be easily represented in these orthogonal curvilinear coordinates.

Spherical and cylindrical coordinates are particular cases of orthogonal curvilinear coordinates.

Homogeneous coordinates

Main article: Uniform coordinates

In mathematics, and more specifically in projective geometry, homogeneous coordinates are an instrument used to describe a point in projective space. They were introduced by the German mathematician August Ferdinand Möbius in the year 1837.

They can also be used as an alternative coordinate system for working in Euclidean space, as Euclidean space can be seen as a subset of projective space. In this way, homogeneous coordinates are widely used in infographics for the representation of scenes in three dimensions. Its matrix form notation is used in 3D graphics programming libraries such as OpenGL and Direct3D.

In homogeneous coordinates, every two-dimensional point is defined by three coordinates, so that a point of dimensions $(x,y)$ , represented by the Terna

${displaystyle left(lambda x,lambda y,lambda right),quad lambda neq 0}$

Two-dimensional coordinates can be found more easily if ${displaystyle lambda =1}$ by simplification. In three dimensions, the same usually happens.

A consequence of this writing is that a proper point can be written in infinite ways, since it is determined by an equivalence relation between the point in question and those others contained in the line it generates.

The basic idea is to extend the Euclidean plane (in the two-dimensional case) to the projective plane. This implies the consideration of improper points, or infinity. An improper point is one where $λ = 0$ , and is determined by the direction of a line, contained in the projective plane.

Other commonly used systems

Some other common coordinate systems are as follows:

Curviline coordinates are a generalization of the coordinate systems in general; the system is based on the intersection of curves.
- Orthogonal coordinates: The coordinate surfaces are at straight angles.
- Oblique coordinates: The coordinate surfaces are not orthogonal.
The log-polar coordinate system represents a point in the plane by the logarithm of the distance to the origin and an angle measured from a reference line that intersectes the origin.
The plückerian coordinates are a way to represent lines in the three-dimensional euclide using a sixth pair of numbers as homogeneous coordinates.
Generalized coordinates are used in the treatment of lagrangiana mechanics.
Canonical coordinates are used in the treatment of hamiltonian mechanics.
The barycentric coordinates (n-simplex) are used to represent ternary diagrams and more generally in the analysis of triangles. They were introduced for the first time by August Möbius, who resolved the question about the center of gravity of the masses located in the vertices of the triangle. They are related invariants, representing a special case of homogeneous general coordinates. A point with bariccentric coordinates is in a vector space $n$ - dimensional. ${displaystyle E^{n}}$ and the actual coordinates in this case refer to a fixed system of points that are not in the subspace ${displaystyle (n-1)}$ - dimensional. Bariccentric coordinates are also used in algebraic topology regarding the points of the simplex.
Trilineal coordinates are one of the homogeneous coordinate samples and are based on a given triangle, so that the position of a point is determined in relation to the sides of this triangle, mainly by the value of the distance from them, although other variations are possible. Trilineal coordinates can be converted to barycentric coordinates with relative ease; they are also converted into two-dimensional rectangular coordinates, for which the corresponding formulas are used. They are used in the context of triangles.
Biangular coordinates. In mathematics, the biangular coordinates are a system of coordinates of the plane where ${displaystyle C_{1}}$ and ${displaystyle C_{2}}$ are two fixed points, and the position of a point P not aligned with ${displaystyle {overline {C_{1}C_{2}}}}$ is determined by the angles ${displaystyle angle PC_{1}C_{2}}$ and ${displaystyle angle PC_{2}C_{1}}$ . This type of coordinates was first examined by Lazare Carnot, who published its results in 1803.
Bipolar coordinates. They are a two-dimensional orthogonal coordinate system based on the circumferences of Apollonius. Confusingly, the same term is also sometimes used to designate the bicentric coordinates. In addition, there is a third system also based on two poles (biangular coordinates).
The bicentric coordinates (also called two-centered coordinates) are a coordinate system, based on two coordinates that give the distances from two fixed centers, $c_{1}$ and $c_{2}$ . This system is very useful in some scientific applications (such as calculating the electric field of a dipole in a plane).
Conical coordinates: They are a three-dimensional orthogonal system consisting of concentric spheres, which are described by their radio, and two families of perpendicular cones located along the axes ${displaystyle Oxland Oz}$ .
Parabolic coordinates: They are a two-dimensional orthogonal coordinate system in which the coordinate lines are confocal parables. A three-dimensional version of parabolic coordinates is obstinated by the rotation of the two-dimensional system on the axis of symmetry of parables. Parabolic coordinates are useful in many applications, such as in the treatment of the Stark effect and in the theory of edge potential.
Projective coordinates. They are called according to the projective space ${displaystyle Pn(K)}$ on which they are defined, and represent a bi-univocal correspondence between their elements and classes of finite subsets of body elements $K$ , characterized by equivalence and ordering properties. To determine the projective coordinates of the projective subspaces, it is sufficient to determine the corresponding coordinates of the projective space points. In the general case, with respect to any basis, the projective coordinates are introduced by purely projective means.
The coordinates of Rindler are mainly used within the framework of relativity theory and describe that part of the flat space-time, which is usually called Minkowski space. In the special theory of relativity, a particle that accelerates evenly is in hyperbolic motion, and for each of these particles in the coordinates of Rindler you can choose a reference point in relation to the one that is at rest.
A toroidal coordinate system is a three-dimensional orthogonal coordinate system that is obtained when rotating a two-dimensional bipolar coordinate system around a shaft that separates its two focus. The focus of the bipolar system, respectively, becomes a ring with radio $a$ which is on the plane ${displaystyle Oxy}$ the toroidal coordinate system, while the axis ${displaystyle Oz}$ becomes the axis of rotation of the system. The focal ring is also sometimes called the base circle.
Cylindrical parabolic coordinates: They are a three-dimensional orthogonal coordinate system obtained as a result of a spatial transformation of a two-dimensional parabolic coordinate system. Confocal parabolic revolution surfaces, respectively, serve as coordinate surfaces. Cylindrical parabolic coordinates are related to rectangular coordinates in a certain way and can be applied in several areas of scientific research.

There are ways to describe curves without coordinates, using intrinsic equations that use invariant quantities like curvature and arc length. These include:

Whewell's equation relates the arch length and tangential angle.
The equation of Cesàro relates the length of arch and curvature.

Coordinates of geometric objects

Coordinate systems are often used to specify the position of a point, but they can also be used to specify the position of more complex shapes such as lines, planes, circles, or spheres. For example, Plückerian coordinates allow us to determine the position of a straight line in space. When necessary, the type of figure being described is used to distinguish the type of coordinate system, for example the term coordinates of line is used for any coordinate system that specifies the position of a straight line.

It may happen that the coordinate systems for two different sets of geometric figures are equivalent in terms of their analysis. An example of this are the homogeneous coordinate systems for points and lines in the projective plane. The two systems in a case like this are said to be dual. Dual systems have the property that the results of one system can be carried over to the other, since these results are just different interpretations of the same analytical result; this is known as the principle of duality.

Coordinate changes

In solving physical and mathematical problems, the strategy of changing coordinates is common. In essence, a change of coordinates means changing the variables on which the problem a depends, to other different coordinates in which the problem can have an equivalent but simpler form, which allows finding the solution more easily.

Since there are often many possible coordinate systems to describe geometric figures, it is important to understand how they relate. These relationships are described by coordinate transformations that give formulas for the coordinates of a system in terms of the coordinates of another system. For example, on the plane, if the Cartesian coordinates ${displaystyle (x,y)}$ and the polar coordinates ${displaystyle (r,theta)}$ have the same origin, and the polar axis is the positive axis of $x$ , then the transformation of coordinates from the polar coordinates to the Cartesians is given by ${displaystyle x=rcdot cos(theta)land y=rcdot sin(theta)}$ .

More formally a change of coordinates can be represented by dipheomorphism or two-and-differentiable application (also inversely differentiated) between two sets of $mathbb {R} ^{n}$ , here called $A$ and $B$ :

${displaystyle {begin{matrix}phi:&Asubset mathbb {R} ^{n}&longrightarrow &Bsubset mathbb {R} ^{n}\&mathbf {x} &longmapsto &mathbf {y} =phi (mathbf {x})end{matrix}}qquad land qquad det Dphi ={frac {partial (y^{1},dotsy^{n})}{partial (x^{1},dotsx^{n})}}neq 0}$

This change of variable allows, for example, to rewrite integrals as follows:

$int _{{Dsubset B}}f({mathbf {y}}) d^{n}{mathbf {y}}=int _{{phi ^{{-1}}(D)}}(fcirc phi)({mathbf {x}}) |det Dphi ({mathbf {x}})| d^{n}{mathbf {x}}=int _{{{tilde {D}}}}{tilde {f}}({mathbf {x}}) Jd^{n}{mathbf {x}}$

Where:

f({mathbf {y}}),{tilde {f}}({mathbf {x}})=(fcirc phi)({mathbf {x}})

represents the function that aims to be integrated expressed in the old and new coordinates.

J=|det Dphi ({mathbf {x}})|

It's the bogey of the change of coordinates.

D,{tilde {D}}=phi ^{{-1}}(D)

is the domain of integration expressed in the old and new coordinates.

To transform or rewrite differential equations in terms of the new coordinates, the tensor transformation laws are used:

${displaystyle {frac {partial f(mathbf {y})}{partial y^{i}}}=sum _{k=1}^{n}{frac {partial x^{k}}{partial y^{i}}}{frac {partial f(phi (mathbf {x}))}{partial x^{k}}}}$

Coordinates of straight lines, curves, planes and surfaces

coordinate surfaces of the three-dimensional paraboloidal coordinates

In two dimensions, if one of the coordinates in a point coordinate system is held constant and the other coordinate is allowed to vary, then the resulting curve is called a coordinate curve. In the Cartesian coordinate system, coordinate curves are actually straight lines, which is why they are called coordinate lines. Specifically, they are the lines parallel to one of the coordinate axes. For other coordinate systems the coordinate curves may be general curves. For example, the coordinate curves in polar coordinates obtained by holding r constant are the circles centered at the origin. A coordinate system for which some coordinate curves are not straight lines is called a curvilinear coordinate system. This procedure does not always make sense, for example coordinate curves do not exist in homogeneous coordinate systems.

In three-dimensional space, if one coordinate is held constant and the other two are allowed to vary, the resulting surface is called a coordinate surface. For example, the coordinate surfaces that are obtained by keeping ρ constant in the spherical coordinate system are the spheres with center at the origin. In three-dimensional space the intersection of two coordinate surfaces is a coordinate curve. In the Cartesian coordinate system we can speak of coordinate planes.

Likewise, the coordinate hypersurfaces are the spaces ${displaystyle (n-1)}$ dimensionals that result from setting a single coordinate of a system $n$ coordinates.

Coordinate origin

Main article: Origin of coordinates

Origin of a two-dimensional Cartesian coordinate system

The origin of coordinates is the reference point of a coordinate system. At this point, the value of all system coordinates is zero — for example, ${displaystyle (0,0)}$ in $mathbb {R} ^{2}$ or $(0,0,0)$ in ${mathbb {R}}^{3}$ - However, in some coordinate systems it is not necessary to establish null and void all coordinates. For example, in a system of spherical coordinates it is sufficient to establish the null radio ${displaystyle (rho =0)}$ , the values of latitude and longitude being indifferent.

In a Cartesian coordinate system, the origin is the point where the axes of the system separate.

Contenido relacionado

Más resultados...