Convolution

Convolution and correlation. The symmetry of the function f makesg↓ ↓ f{displaystyle g*f}Andf↓ ↓ g{displaystyle f*g}be identical operations with identical results.

Convolution in an optical device (fluorescence microscope, longitudinal cutting of a 3D image).

Convolution of two square pulses (the resulting function is a triangular pulse).

Convolution of a square pulse (as input signal) with the response to the impulse of a capacitor to obtain the output signal (response of the capacitor to that signal).

Visual explanation of the convolution: # Each function is expressed in terms of a fictitious variable τ. # Reflect one of the functions: g(τ) → g(-τ). # It adds a time of displacement t, which allows g(t - τ) to slide along the axis τ. # Make t equal to -∞ and slide it to +∞. When the two functions are intersected, you will find the integral of your product. In other words, the weighted average shifted from the f(τ) function is calculated, where the weight function is g(-τ). The resulting wave form (not shown here) is the convolution of the functions f and g. If f(t) is a unitary impulse, the result of this process is simply g(t), which is therefore called the response of the impulse.

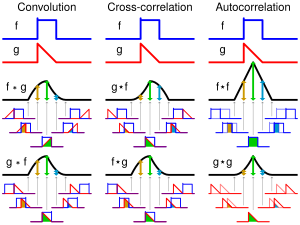
In mathematics, and in particular functional analysis, a convolution is a mathematical operator that transforms two functions f and g into a third function which in a sense represents the extent to which f and a translated and inverted version of g overlap. A convolution is a very general type of moving average, as can be seen if one of the functions is taken as the characteristic function of an interval.

Definition

The Convolution of f{displaystyle f,} and g{displaystyle g,} denotes f↓ ↓ g{displaystyle f*g,}. It is defined as the product integral of both functions after moving one of them a distance t{displaystyle t}.

(f↓ ↓ g)(t)=.∫ ∫ − − ∞ ∞ ∞ ∞ f(MIL MIL )g(t− − MIL MIL )dMIL MIL {displaystyle (f*g) {stackrel {mathrm {} {=}}}int _{-infty }^{infty }f(eta)g(t-eta)deta }

The interval of integration will depend on the domain over which the functions are defined. In the case of a finite range of integration, f and g are often considered to be extended, periodically in both directions, such that the term g(t - η) does not imply a range violation. When these periodic domains are used the convolution is sometimes called cyclic. Of course, it is also possible to zero-extend the domains. The name used when these zero-extended or infinite domains are put into play is linear convolution, especially in the discrete case that will be presented below.

Yeah. X{displaystyle X} e And{displaystyle Y} are two independent random variables with probability density functions f and g, respectively, then the probability density of the sum X + And will be given by the convolution f ♪ g.

For discrete functions a discrete form of convolution can be used. This is:

f[chuckles]m]↓ ↓ g[chuckles]m]=␡ ␡ nf[chuckles]n]g[chuckles]m− − n]{displaystyle f[m]*g[m]=sum _{n}{f[n]g[m-n]},}

When two polynomials are multiplied, the coefficients of the product are given by convolving the original sequences of coefficients, in the sense given here (using zero-extensions as mentioned).

Generalizing the previous cases, the convolution can be defined for any two square integrable functions defined on a locally compact topological group. A different generalization is the convolution of distributions.

Use

Convolution and related operations are found in many engineering and mathematical applications.

• In statistics, as a weighted mobile average.
• In theory of probability, the probability distribution of the sum of two independent random variables is the convolution of each of its probability distributions.
• In optics, many types of stains are described with convolutions. A shadow (e.g. the shadow on the table when the hand is between this and the source of light) is the convolution of the form of the source of light that creates the shadow and the object whose shadow is projected. A blurred photograph is the convolution of the correct image with the blurred circle formed by the iris diaphragm.
• In acoustics, an echo is the convolution of the original sound with a function that represents the various objects that reflect it.
• In electrical engineering, electronics and other disciplines, the output of a linear system (stationary or time-invariant or space-invariant) is the convolution of the entry with the response of the system to an impulse (see animations).
• In physics, where there is a linear system with a superposition principle, a convolution operation appears.

Convolution Types

Discrete convolution

When it comes to making digital signal processing it makes no sense to talk about conversions by strictly applying the definition as only discrete time values are available. A numerical approach is therefore necessary. To perform the convolution between two signals, the function area will be evaluated:x(Δ Δ )↓ ↓ h(t− − Δ Δ ){displaystyle x(tau)*h(t-tau),}. For this purpose, both signals are available at the time nt{displaystyle nt,}The one you'll call x[chuckles]k]{displaystyle x[k],} and h[chuckles]n− − k]{displaystyle h[n-k],} (where n and k are integers). The area is, therefore,

and[chuckles]n]=␡ ␡ k=− − ∞ ∞ ∞ ∞ t⋅ ⋅ x[chuckles]k]⋅ ⋅ h[chuckles]n− − k]=t⋅ ⋅ [chuckles]␡ ␡ k=− − ∞ ∞ ∞ ∞ x[chuckles]k]⋅ ⋅ h[chuckles]n− − k]]{displaystyle and[n]=sum _{k=-infty }^{infty }tcdot x[k]cdot h[n-k]=tcdot {left[sum _{k=-infty }^{infty }x[k]cdot h[n-k]right]

Discreet convolution is determined by a sampling interval t=1{displaystyle t=1}:

and[chuckles]n]=x[chuckles]n]↓ ↓ h[chuckles]n]=␡ ␡ k=− − ∞ ∞ ∞ ∞ x[chuckles]k]⋅ ⋅ h[chuckles]n− − k]{displaystyle y[n]=x[n]*h[n]=sum _{k=-infty }^{infty }x[k]cdot h[n-k]}}}

Circular convolution

When a function gT{displaystyle g_{T}} regular period T{displaystyle T}, then for those functions f{displaystyle f} for which there exists f↓ ↓ gT{displaystyle f*g_{T}}, its convolution is also periodic and equal to:

(f↓ ↓ gT)(t)≡ ≡ ∫ ∫ t0t0+T[chuckles]␡ ␡ k=− − ∞ ∞ ∞ ∞ f(Δ Δ +kT)]gT(t− − Δ Δ )dΔ Δ ,{displaystyle (f*g_{T})equiv int _{t_{0}}{t_{0}+T}left[sum _{k=-infty }^{infty }f(tau +kT)right]g_{T}(t-tau) dtau,}}

where t0{displaystyle t_{0}} is arbitrarily chosen. The sum under the integration is called periodic extension of the function f{displaystyle f}. Yeah. gT{displaystyle g_{T}} is a regular extension of another function g{displaystyle g}, then f↓ ↓ gT{displaystyle f*g_{T}} is called circular, cyclicalor periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic regular periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic periodic of f{displaystyle f} and g{displaystyle g}.

Method for calculating circular convolution:

1. They have two circles, one outside and another inside. They are turning the inner circle and adding their values.
2. If the two circles have different sizes, then the smallest one is added "0" at the beginning, at the end or at the beginning and end.

[L >= L1 + L2-1]

Properties

The properties of the different convolution operators are as follows:

Commutativity

f↓ ↓ g=g↓ ↓ f{displaystyle f*g=g*f,}

Associativity

f↓ ↓ (g↓ ↓ h)=(f↓ ↓ g)↓ ↓ h{displaystyle f*(g*h)=(f*g)*h,}

Distributivity

f↓ ↓ (g+h)=(f↓ ↓ g)+(f↓ ↓ h){displaystyle f*(g+h)=(f*g)+(f*h),}

Associativity with scalar multiplication

a(f↓ ↓ g)=(af)↓ ↓ g=f↓ ↓ (ag){displaystyle a(f*g)=(af)*g=f*(ag),}

for all complex numbers a{displaystyle a}.

Rule of Derivation

D(f↓ ↓ g)=Df↓ ↓ g=f↓ ↓ Dg{displaystyle {mathcal {D}}(f*g)={mathcal {D}f*g=f*{mathcal {D}}g,}

where Df denotes the derivative of f or, in the discrete case, the difference operator

Df(n)=f(n+1)− − f(n){displaystyle {mathcal {D}}f(n)=f(n+1)-f(n)}.

Convolution Theorem

F(f↓ ↓ g)=(F(f))⋅ ⋅ (F(g)){displaystyle {mathcal {F}}(f*g)={({mathcal {F}}(f))cdot ({mathcal {F}}(g)}}}}}}}}}}

where F{displaystyle {mathcal {F}}} denotes Fourier Transformation f. This theorem is also fulfilled by the Laplace Transformation.

Convolutions with Dirac deltas

f(t)↓ ↓ δ δ (t)=f(t){displaystyle f(t)*delta (t)=f(t),}

f(t)↓ ↓ δ δ (t− − t0)=f(t− − t0){displaystyle f(t)*delta (t-t_{0})=f(t-t_{0}),}

f(t− − t1)↓ ↓ δ δ (t− − t0)=f(t− − t0− − t1){displaystyle f(t-t_{1})

δ δ (t− − t1)↓ ↓ δ δ (t− − t2)=δ δ (t− − t1− − t2)(t-t_{1})

Convolution matrix

Sometimes it is useful to see convolution as a matrix product. Sea x{displaystyle mathbf {x} } a discreet function m{displaystyle m} elements, h{displaystyle mathbf {h} } a discreet system n{displaystyle n} elements, and and{displaystyle mathbf {y} } the convolution of both m+n− − 1{textstyle m+n-1} elements: and=h↓ ↓ x{displaystyle mathbf {y} =mathbf {h}. Then you can define a matrix A{displaystyle mathbb {A} } (the convolution matrix, which is a Toeplitz matrix) such that and=xA{textstyle mathbf {y} =mathbf {x} mathbb {a} }:

and=(and1and2and3...... andm+n− − 1)=(x1x2x3...... xm)[chuckles]h1h2h3...... hn0...... ...... ...... 00h1h2h3...... hn0...... ...... 000h1h2h3...... hn0...... 0 0...... ...... ...... 0h1h2h3...... hn]### #############################################################################################################################################################################################################################################################

Example:

Sea x=(4517){displaystyle mathbf {x} ={begin{pmatrix}4 fake5 fake1 fake7end{pmatrix}}}} and be h=(1231){displaystyle mathbf {h} ={begin{pmatrix}1 fake2 fake3 fake1end{pmatrix}}}} then the convolution matrix will be:

[chuckles]1231000012310000123100001231]{display {begin{bmatrix}1 exposesstyle}1 exposes3 hypos0 hypos0 fake0 fake1 fake0 fake0 fake0 fake0 fake1 fake2 fake2 fake1 fake0 fake0 fake0 fake1 fake2 fake3 fake1\end{bmatrix}}}}}}

You can see how zeros are added to both sides. This is done to be able to equalize and thus be able to do the convolution. This technique is known as zero padding.

Padded with zeros

It consists of extending numeric spaces by adding null values (zeros) to their ends before performing a convolution. It can be in source space or in the spectrum of a signal. In the latter case, the frequency domain of the magnitude of the signal is increased, but the resolution is not improved.

Group convolutions

If G is a certain group endowed with measure m (for example, a locally compact Hausdorff topological group with the Haar measure) and if f and g are real -or complex- valued and m-integrable functions of G, so their convolution can be defined as

(f↓ ↓ g)(x)=∫ ∫ Gf(and)g(xand− − 1)dm(and){displaystyle (f*g)(x)=int _{G}f(y)g(xy^{-1}),{text{d}m(y),}

In this case it is also possible to give, for example, a convolution theorem, which however is much more difficult to present and requires representation theory for these types of groups as well as the Peter-Weyl Theorem of harmonic analysis. It is very difficult to do such calculations without more structure, and Lie groups are the frameworks where things should be done.