Continuous function

ImprimirCitar

In mathematics, a continuous function is one for which, intuitively, small variations in the values of the function occur for nearby points in the domain; although strictly speaking, in a metric space as in a real variable, it means that small variations of the function imply that the points must be close. If the function is not continuous, it is said to be discontinuous. Informally, a continuous function from ℝ to ℝ is one whose graph can be drawn without lifting the pencil from the paper (more formally its graph is a connected set).

The continuity of functions is one of the basic concepts of mathematical analysis and general topology. This article mainly describes the continuity of real functions of a real variable.

Real functions of a real variable

Informally speaking, a function f defined on an interval I is continuous if the curve that represents it, that is, the set of points (x, f(x)), with x in I, it is constituted by a continuous line, that is to say, a line that is not broken, nor does it have "holes" nor "jumps", as in the figure on the right.

The interval I of x is the domain of definition of f, defined as the set of all values of x for which f(x) exists.

The interval J of y is the range (also known as the image) of f , the set of y-values, taken as y = f(x). Write J = f(I). Note that in general, it is not the same as the codomain (only if the function in question is surjective.)

The largest element of J is called the absolute maximum of f in I, and the smallest value of J is its absolute minimum in the domain I.

Continuity of a function at a point

Definition of continuity at a point

A function f is continuous at a point x₀ that belongs to the domain of the function.

if:

0quad exists delta >0;}" xmlns="http://www.w3.org/1998/Math/MathML">Русский Русский ε ε ▪0consuming consuming δ δ ▪0{displaystyle forall varepsilon 0quad exists delta /20050;}0quad exists delta >0;}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/73449d57a9317f79d3dc7d199d0869b995763257" style="vertical-align: -0.338ex; width:16.207ex; height:2.343ex;"/>

such that for all x in the domain of the function

<math alttext="{displaystyle |x-x_{0}|<delta quad Rightarrow quad |f(x)-f(x_{0})|日本語x− − x0日本語.δ δ ⇒ ⇒ 日本語f(x)− − f(x0)日本語.ε ε {displaystyle Δx-x_{0} implies quad Rightarrow quad Δf(x)-f(x_{0})<img alt="{displaystyle |x-x_{0}|<delta quad Rightarrow quad |f(x)-f(x_{0})|

This can be written in terms of limits as follows; if x₀ is the point of the domain of the function that is the point of accumulation of the same, then f is continuous x₀ Yes and only if ${displaystyle lim _{xto x_{0}}f(x)=f(x_{0})}$ When x₀ is a point of the domain that is not of accumulation of the same, that is, is isolated point of the domain, the definition is trivially fulfilled, then all function is continuous in the isolated points of its domain. For example, the successions of real numbers are a real variable function case whose domain is the set of natural numbers. As all the points of the domain of a succession are isolated points of it, it is concluded that all succession is a continuous function. On the other hand, it makes no sense to talk about whether a function is or does not continue at a point that does not belong to the domain of it. For example, the f(x)=1/x function is continuous at all points of your domain (note that zero is not in the function domain). In zero, as it is not in the domain, we cannot speak of whether it is continuous or whether it is not since the definition of continuity at a point and, therefore, the possibility of deciding whether a function is or does not continue at that point, part of a point of the domain of the function before defining the continuity at it. Let us not forget that the domain of a function does not have to be an interval. For example, the domain of the function ${displaystyle f(x)={sqrt {cos(2pi x)-1}}}$ That's it. $mathbb Z$ , the whole numbers.

OBSERVATION:
For applications $mathbb{R}$ in $mathbb{R}$ It is common to see that a function is said $f$ is continuous at a point x₁ if it exists f (x)₁)if there is a limit (x) When x towards x₁ on the right, if there is the limit (x) When x towards x₁ on the left, and also both match f (x)₁). This would imply that, given a function, if not defined at a point, it is not continuous in it, reaching a situation like the following: The function ${displaystyle f:(0,1)longrightarrow mathbb {R} }$ defined as ${displaystyle f(x)=x}$ is not continuous at 0 because it is not defined at that point, but it is not continuous at 3 or 5. This non-satisfactory definition of continuity is very widespread, but it is necessary to remember the necessary requirement to be able to speak of continuity that the point in which continuity is studied belongs to the domain. If it is not in the domain, but it is a build-up point, we can talk about whether or not it can be extended with continuity to that point, but we cannot say that the function is discontinuous at that point (the extended function could be discontinuous, since by incorporating that point into the domain, it makes sense to consider the study of continuity in it).

Thus, a function f continues at a point in its domain x₁ which, moreover, is a point of accumulation of the same, implies the following:

{displaystyle {color {Blue}(7)};f(x_{1})=L_{(x_{1})}left{{begin{array}{l}{color {Blue}(5)};L_{(x_{1})}=L_{(x_{1})}^{+}=L_{(x_{1})}^{-}left{{begin{array}{l}{color {Blue}(3)};exists ;L_{(x_{1})}^{+}land exists ;L_{(x_{1})}^{-};left{{begin{array}{l}{color {Blue}(1)};exists ;L_{(x_{1})}^{+}={displaystyle lim _{xto {x_{1}}^{+}}f(x)}\\{color {Blue}(2)};exists ;L_{(x_{1})}^{-}={displaystyle lim _{xto {x_{1}}^{-}}f(x)}end{array}}right.\{color {Blue}(4)};L_{(x_{1})}^{+}=L_{(x_{1})}^{-}end{array}}right.\{color {Blue}(6)};exists f(x_{1})end{array}}right.}

1. There is the limit on the right:

{displaystyle exists lim _{xto x_{1}^{+}}f(x)in mathbb {R} }

2. There is the limit on the left:

{displaystyle exists lim _{xto x_{1}^{-}}f(x)in mathbb {R} }

3. The limit on the right and the limit on the left coincide:

{displaystyle lim _{xto x_{1}^{-}}f(x)=lim _{xto x_{1}^{+}}f(x)}

4. If the limit on the right and on the left exist and their values coincide, the function has a limit at this point:

{displaystyle lim _{xto x_{1}}f(x)=lim _{xto x_{1}^{-}}f(x)=lim _{xto x_{1}^{+}}f(x)}

5. There is f(x₁):

{displaystyle exists f(x_{1})}

6. The limit and the value of the function coincide:

{displaystyle lim _{xto x_{1}}f(x)=f(x_{1})}

A function is said to be continuous on an interval if it is continuous at all points.

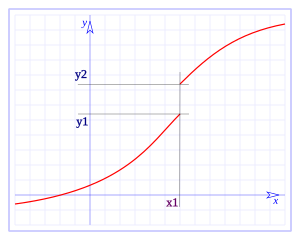
If f(x₁)= y₁, the continuity at x₁ is expressed like this:

{displaystyle lim _{xto x_{1}}f(x)=y_{1}}

paraphrasing, when x approaching x₁, f(x) approaching and₁. By definition of limits, this means that for every open interval Jfocused on and₁, there is an open interval Ifocused on x₁, such that ${displaystyle f(I)in J}$ .

If f is not continuous at a point, the theorem is faulty. Indeed, not every interval I around x₁ has its image in an interval J centered at y₁, with a radius less than the step of f, no matter how small this interval is, there are values of x of the interval I around x₁ which has its image in an interval K centered at y ₂, where y₁ and y₂ are distinct values, that is: x has images that fall outside of J.

The advantage of this definition is that it can be generalized to any topological space.

Lateral continuity

A function $f$ That's it. continue on the left at the point $x_{1}$ if the lateral boundary on the left and the function value at the point are equal. I mean:

{displaystyle lim _{xto x_{1}^{-}}f(x)=f(x_{1})}

as in the figure.

A function $f$ That's it. Continue on the right at the point $x_{1}$ if your lateral limit on the right and the function value at the point are equal. I mean:

{displaystyle lim _{xto x_{1}^{+}}f(x)=f(x_{1})}

A function $f$ That's it. continuous at a point Yeah. continue on the left and it is Continue on the right. This is:

{displaystyle lim _{xto x_{1}^{-}}f(x)=lim _{xto x_{1}^{+}}f(x)=f(x_{1})}

Continuity of a function on an open interval: (a,b)

A value c belongs to an open interval I, with extreme left a and extreme right b, represented I= (a,b) if:

<math alttext="{displaystyle a<c a.c.b{displaystyle a prescriptionb;} <img alt="{displaystyle a<c

A function, f is continuous on an open interval I= (a,b), if and only if the function is continuous at all points in the interval, that is to say:

${displaystyle forall cin I=(a,b):quad lim _{xto c}f(x)=f(c)}$

Continuity of a function on a closed interval: [a,b]

A value c belongs to a closed interval I, with extreme left a and extreme right b, represented I= [a,b] if:

${displaystyle aleq cleq b;}$

A function f is continuous on a closed interval [a, b] if the function is continuous on the open interval (a,b) and is continuous to the right of a and continuous to the left of b:

${displaystyle forall cin I=[a,b]:quad lim _{xto c}f(x)=f(c)quad land quad lim _{xto a^{+}}f(x)=f(a)quad land quad lim _{xto b^{-}}f(x)=f(b)}$

Some important continuous functions

Sinus and cosine functions

Polynomial, trigonometric functions: sine and cosine, exponentials, and logarithms are continuous in their respective domains of definition.

The parabola, as a polynomial function, is an example of a function that is continuous throughout the entire real domain.

The graph shows the sine function, which is periodic, bounded and continuous in the entire real domain, given its periodic nature, seeing just one of the cycles is enough to check the continuity, because the rest of the cycles are exactly the same.

Functions defined by intervals

Main article: Function defined to pieces

Functions defined for different intervals of x, can be discontinuous at interval change points, such as:

The entire Function part of x, E(x) where E(x) is the largest integer below or equal to xsuch that:

E(x) ≤ x E()x+ 1.

Its graph is a succession of horizontal segments at different heights. This function is not continuous on the integers, since the left and right limits are different, but it is continuous on the open segments (n, n+1) where it is constant.

Other functions defined by intervals are:

Unital step function

Function sign

Rational Function

Main article: Rational role

Rational functions are continuous on a suitable interval. An example of this is the function inverse of x:

${displaystyle f(x)={frac {1}{x}}}$

This function is a hyperbole composed of two sections. x 0 and x  0. As you can see, it is continuous throughout the domain ${displaystyle left(-infty0right)cup left(0,+infty right)}$ because it is not defined in x= 0. If the domain of the function is extended to R (Given an arbitrary value to f(0) the function will be discontinuous.

Theorems about continuous functions

These are some of the most important theorems about continuous functions.

Theorem of Weierstrass: Yes f is continuous $[a,b]$ then. f has at least a maximum and at least a minimum in that interval.
Bolzano Theorem: Yes f is continuous $[a,b]$ and $<math alttext="{displaystyle f(a)<0f(a).0.f(b){displaystyle f(a)} <img alt="{displaystyle f(a)<0$ or $<math alttext="{displaystyle f(b)<0f(b).0.f(a){displaystyle f(b) backwards <img alt="{displaystyle f(b)<0$ , then it exists ${displaystyle cin (a,b)}$ such as ${displaystyle f(c)=0}$
Intermediate value theorem: Yes f is continuous $[a,b]$ and $<math alttext="{displaystyle k:,f(a)<kk:f(a).k.f(b){displaystyle k:,f(a) ingredientk(b)} <img alt="{displaystyle k:,f(a)<k$ then it exists ${displaystyle cin (a,b)}$ such as ${displaystyle f(c)=k}$
Attachment: Yes f is a function on a compact set then, the function has a maximum or a minimum (on an open set you have the following counterexample the function ${displaystyle f(x)=1/x}$ It's continuous on ${displaystyle (0,1)}$ but it is not sheltered.

Derivative and Continuity

Differential functions are continuous. If a function is differentiable at x=a then it is continuous at x=a. So continuity is a necessary condition for differentiability.

Demonstration
: ${displaystyle f(x)-f(a)=f(x)-{{f(a)}^{}}^{}}$ ${displaystyle f(x)-f(a)={frac {(f(x)-f(a))(x-a)}{(x-a)}}}$ ${displaystyle f(x)={frac {(f(x)-f(a))(x-a)}{(x-a)}}+f(a)}$ ${displaystyle lim _{xto a}f(x)=lim _{xto a}{frac {(f(x)-f(a))}{(x-a)}}lim _{xto a}(x-a)+lim _{xto a}f(a)}$ ${displaystyle f'(a)lim _{xto a}(x-a)+lim _{xto a}f(a)=f'(a)cdot 0+f(a)=f(a)}$

It is important to note that reciprocal is not valid; that is, nothing can be said about the derivability of a continuous function. A clear example of this situation is the absolute value function f(x)= that although it is continuous in all its domain is not derivable in x= 0. There are even continuous functions in everything $mathbb{R}$ but not derivable at any point (the functions of the Brownian movement verify this with probability 1).

Continuity class

A function ${displaystyle f:Omega subset mathbb {R} longrightarrow mathbb {R} }$ It is said that:

It's class. ${displaystyle C^{0}(Omega),}$ when it is continuous throughout the domain $Omega$ .
It's class. ${displaystyle C^{k}(Omega),}$ if it is defined in all domain $Omega$ along with their derivatives to order ${displaystyle kgeq 1}$ and they are all continuous.
It's class. ${displaystyle C^{infty }(Omega),}$ if you have continuous derivatives of any order. Note that functions of this type are not necessarily analytical.
A function is class ${displaystyle C^{-1}(Omega),}$ if it is derived in the sense of distributions of a class function ${displaystyle C^{0}(Omega),}$ .
A generalized function is said to be class ${displaystyle C^{-k}(Omega),}$ if it is the derivative k-thousand in the sense of distributions of a class function ${displaystyle C^{0}(Omega),}$ .

Any polynomial function of a variable is a class function ${displaystyle C^{infty }(mathbb {R})}$ . The widespread denomiated delta function of Dirac is a class function ${displaystyle C^{-2}(mathbb {R}),}$ since it is the second derivative of the ramp function that is continuous, and the first derivative of the Heaviside step function that is class ${displaystyle C^{-1}}$

Examples that show that there are class functions ${displaystyle C^{k}(Omega),}$ But they're not class. ${displaystyle C^{k+1}(Omega),}$ . The classic examples are ${displaystyle f_{k}(x)=x^{k}operatorname {sen}(1/x)}$ .

Continuous functions on topological spaces

Sean. ${displaystyle (X,T_{X})}$ e ${displaystyle (Y,T_{Y})}$ two topological spaces. An application ${displaystyle f:Xlongrightarrow Y}$ is said to be Continue Yes:

${displaystyle f^{-1}(G)}$ It's an open $X$ Whatever the open $G$ of ${displaystyle Y}$ . This is the continuity seen globally, the following is the continuity at a domain point.

This definition is reduced to the ordinary definition of continuity of a function ${displaystyle f:mathbb {R} ^{n}to mathbb {R} ^{m}}$ Yeah. $mathbb {R} ^{n}$ and ${displaystyle mathbb {R} ^{m}}$ is considered the topology induced by euclid distance.

With the same previous notation, if ${displaystyle xin X}$ We'll say $f$ That's it. Continue in $x$ when you get that ${displaystyle f^{-1}(V)}$ is an environment $x$ Whatever the environment $V$ of $f(x)$ .

It is possible then to check that $f$ is continuous if and only if it is continuous $xin X$ , whatever this is, that is, when it is continuous at each of the points of your domain.

Continuous functions on ordinal numbers

The term continuous function in the part of the set theory that refers to the ordinary numbers makes a different sense to that of the functions on topological spaces. Specifically a function F defined on the class of ordinary numbers ${displaystyle mathrm {On} }$ is continuous if for each ordinal limit the following property is fulfilled:

$<math alttext="{displaystyle F(gamma)=bigcup {F(sigma)| sigma F(γ γ )= {F(σ σ )日本語σ σ .γ γ ,σ σ 한 한 On!{displaystyle F(gamma)=bigcup {F(sigma) Ministère sigma Δgamma sigma in mathrm {On} }}}} <img alt="{displaystyle F(gamma)=bigcup {F(sigma)| sigma$

Contenido relacionado

Four color theorem
In graph theory, the four color theorem is a theorem about graph coloring that states the...
Theorem
A theorem is a proposition whose truth is proved. In mathematics, it is any proposition that, based on an assumption affirms a reasonableness that is not...
Subset
In mathematics, a set B is a subset of another set A if all elements of B also belong to A . We then say that B is contained within...
Más resultados...
Te puede interesar