Complex (chemistry)

In chemistry, a complex is an entity that is formed by an association that involves two or more components joined by a type of chemical bond, the coordination bond, which is normally a little weaker than a typical covalent bond.
By historical custom, the term complex is used mainly to describe that type of molecular structure that is usually formed by a central atom (which is often a metal cation) that is found bound to other surrounding molecular entities called ligands. This last meaning is also known as coordinating entity.
The term is also used to refer to a huge number of unstable or metastable structures that participate as intermediaries in different reactions; Therefore, it is preferable to use whenever possible a more explanatory term to refer to these compounds. In this sense, the term complex is much broader, but less precise. In inorganic chemistry, for example, it is preferred to use the term coordination entity instead of complex.
The chemistry of complexes has numerous theoretical and practical applications, serving for example: to explain such common details as the color of precious stones; the industrial production of polymers, pigments, colorless and colored glasses; electroplating of metals; formulation of water softeners for household cleaning products and even the treatment of some poisonings and the theoretical basis that allows us to understand most of the enzymatic reactions that allow the existence of life.
Preliminary considerations
The simplest complexes respond to a type of molecular structure that is generally formed by a central group (usually a cation) called the coordination nucleus that has unoccupied valence orbitals, surrounded by a a number of molecules or ions that have unshared pairs of electrons. These unshared electrons can be injected into the empty orbitals of the central group to form coordinate bonds.
Although in general the central group is a cation it can also be a neutral atom, for example a noble gas atom, or a molecule and it can have a positive, negative charge or no charge at all.
Ions or molecules that participate in the molecular structure by injecting their unshared pair of electrons are generically called ligands.
The adduct formed by the central group and the ligands is called coordination entity and the compounds that contain coordination entities in their constitution are called coordination compounds.
A ligand bound to a central atom is said to be coordinated to that atom. The number of electron pairs that the central group is capable of accepting is called the coordination number.
General information
The atoms of metallic elements have a clear tendency to lose electrons to become positively charged ions (cations), this is so because they generally have a high atomic radius in relation to the charge of their nuclei, which makes it possible to Its valence electrons are easily detached. (Because the valence electrons are the ones that are the furthest away from the nucleus, they are the ones that experience the least electrostatic attraction and therefore are the ones that are most easily detached.)
This may lead to the idea that positively charged metal ions (cations) should be very abundant in nature. However, metallic cations are rarely found in a free state in nature, this is so because when they lose one or more electrons their radius decreases and their electrical charge increases. An increase in the charge/radius ratio means a decrease in the thermodynamic stability of a chemical species.
In general, metal cations have such a high charge/radius ratio that they quickly interact with other ions, atoms or molecules, to acquire a structure that is thermodynamically more stable. They achieve this stabilization either by interacting with neutral molecules, which causes an increase in the molecular radius and a consequent decrease in the charge/radius ratio; or with negatively charged ions (anions) which, in addition to causing an increase in the molecular radius, provide additional stability by “relieving” the cation by providing negative charges.
It is common that in these associations, the molecules or ions that provide stability to the central cation act as Lewis bases, that is, that by having one or more unshared pairs of electrons they are capable of "injecting" those electrons into empty orbitals of the cation to increase its stability.
Metal cations are almost always found in nature forming some kind of complex that stabilizes them; Very often the complexing agent is usually the solvent in which they are dissolved.
A good part of the metal salts of the metals of the main and transition groups are hydrated. The waters of hydration act as ligands that surround the metal, bonding through an unshared electron pair of the water. A notable example of this is cobalt salts which are used to 'predict the weather'; In some children's games, in these the cobalt is coordinated by a number of water molecules that changes with the environmental humidity, the change in the coordination of the cobalt causes a change in the color of the salt, from blue to pink by increasing the moisture and vice versa.
Most of the known complex chemistry deals with complexes formed by coordination entities with coordination nuclei that are metallic cations, however it should be clear that there are also complexes in which these coordination nuclei are non-metallic atoms, Either they participate with zero charge, or they are molecules instead of atoms. There are even some in which the nucleus has a negative charge.
History
With the constant progress that chemistry had in its beginnings as an exact science, a series of new compounds were soon synthesized that were very striking, especially due to their colors. These chemical compounds, for lack of a more adequate description, took the names of their creators. This is how they became known, for example, Magnus's salt (2PtCl
2 2NH
3) or Erdmann's salt (KNO
2Co(NO
2)
2 2NH
2). Another of these colorful compounds was Prussian blue, also known as Berliner Blau or Berlin blue, (KCNFe(CN)
2 Fe(CN)
3) produced by Diesbach in Berlin at the beginning of the 18th century Many of the early complexes were used as pigments by the painters of the time.
These compounds had two notable properties that differentiated them from those known up to now: First, the bright color changes associated with their formation, and second, the altered reactivity of the ions involved.
It was not until the middle of the 19th century that chemists began to be interested in the true nature of their constitution and their relation to other simpler compounds.
At first it was found, as can be seen in the formulas expressed above, that these compounds seemed to be formed by the association of other simpler compounds. This led to their identification as "molecular compounds", to differentiate them from "atomic compounds" simpler; and finally, they were given the name COMPLEXES, to differentiate them from simple compounds. To tell the truth, this was an appropriate name for the time, since it was difficult to find a valid structure that could explain all its properties. Along with this, the number of known complexes increased as their study progressed.
The development of models that would explain their nature had to wait for the appearance of valid theories and models for simpler compounds. The fundamental steps in this regard were, firstly, the definition of what was considered a "true" compound, better known as the Law of Definite Proportions, proposed by J.L. Proust in 1799, which establishes that: «a given compound will always be made up of the same proportions of its constituent elements». In other words what we know today as "defined stoichiometry". This first definition was transcendental to separate some compounds from others, especially in the case of complexes.
Then, in 1827, J.J. Berzelius introduced the concept of isomerism, which complements the previous definition but introduces a key question: how do atoms bond with each other? To find an answer to this question, the theory of types was definitive, proposed by Ch. Gerhardt (circa 1853), developed for ammonia by Ch. A. Wurtz in 1849 and expanded and worked on by A. W. Von Hofmann (), today known as "Ammonium Theory"; this theory was a first approximation to explain how the atoms in the abundant "complexes" that contained ammonia.
Simultaneously, the "Combination Force Theory" or "Atomicity Theory" (A first approximation to the current concept of valence, proposed by E. Frankland in 1852 as an extension of the law of definite proportions; this theory establishes that «each element can only be united to a fixed number of other elements» Thus, it could be ensured that the atomicity of zinc was always two and that of nitrogen or phosphorus was always 3 or 5.
F.A. Kekulé in 1858, proposed the notion that many organic compounds had to be the product of the union of carbon atoms together in the form of chains. In addition to what was previously known, this notion necessarily influenced a second model developed in 1869 and successfully supported for several decades by the Scandinavians Blomstrand, professor of Chemistry in Lund (Sweden) and his student Jörgensen, who was later a professor at the University of Copenhagen and one of the foremost experimenters in coordination chemistry. However, Jörgensen himself would have to synthesize the compound that would define the validity of his theory, concluding in the end that his model, known as the chain theory, was incorrect.
The recognition of the true nature of complexes begins with Alfred Werner (1866-1919), professor of Chemistry in Zurich, who demonstrated that the neutral molecules that participated in the formation of a complex (coordinating entity) were directly bound to the metal, such that complex salts such as CoCl
3 6NH
3 should be correctly formulated as [Co(NH
3)
6]3+
Cl−
3. He also showed that profound stereochemical consequences ensued if the molecules or ions (ligands) around the metal were assumed to occupy positions at the vertices of a square or an octahedron.
Alfred Werner, proposed that atoms could simultaneously exhibit more than one type of valence. The first part of his coordination theory, published in 1893, can be summarized in the following three postulates:
- 1. Most chemical elements present two types of valence, primary valence or ionizable union, now known as the number of oxidation and the secondary valence or non-ionizable union, now known as the number of coordination.
- 2. The elements tend to satisfy both their primary valence and their secondary valence.
- 3. The secondary valence or coordination number is distributed in positions defined in the space.
These three postulates gave a satisfactory explanation to the main questions that chemists had been asking about "complexes". Taking as an example for the application of the postulates the well-known series of amines CoCl
3 6NH
3, CoCl
3 5NH
3, CoCl
34NH
3, CoCl
3 3NH
3, we have that the primary valence or oxidation state of cobalt in all cases is 3+, and the secondary valence or coordination number of this ion is 6. The 3+ oxidation state of cobalt is balanced, as is clearly seen in all cases, by 3 chloride ions.In the first example all the chlorides are ionic and are not part of the complex cation [Co(NH
3)
6]3+
; coordination number 6 is satisfied by 6 groups NH
3. In the second example, the coordination number is satisfied by 5 NH
3 and 1 Cl−
, [CoCl(NH
3)
5]2+
and only two chlorides are ionic. In the third case, 4 NH
3 and 2 Cl−
satisfy the coordination number [CoCl
2(NH
3)
4]+
and in the last case it is satisfied by 3 NH
3 and 3 Cl−
, [CoCl
3(NH
3)
3].
The third postulate led Werner to assert that the presence of optical isomerism for complexes of the type [M(AA)
3] (Where AA is a bidentate ligand) was evidence of an octahedral structure and that this isomerism was due to asymmetry of the molecule; some organic chemists tried to refute his hypothesis by arguing that the optical activity was due to the presence of carbon atoms in the structure and that this property was exclusively due to carbon. This controversy led Werner and his group in 1914 to synthesize the most extraordinary complex of the time, hexol ([Co(Co(NH
3)
4)
3(OH)
6]), which did not contain carbon in its structure.
Hexol presented, as is obvious today, optical isomerism, consolidating the coordination theory, and also showing that this isomerism is a function of the symmetry operations of molecules in general and not specific to a single type of atom.
Werner's conclusion established one of the strongest arguments for considering chemistry as one, with general rules, and breaking down artificially imposed walls between organic and inorganic chemistry.
Werner was awarded the Nobel Prize in 1913 for developing his theory of coordination. In his fundamental concepts, this theory is still valid as it allows to correctly explain many of the structural aspects of coordination compounds.
Werner's stereochemical studies were later followed by the ideas of G. N. Lewis and N. V. Sidgwick, who proposed that it was the electrons in the last orbit of an atom that were responsible for chemical bonding and that "a chemical bond it required sharing a pair of electrons» in such a way that the condition that each participating atom in the bond would eventually obtain eight electrons in its outermost shell was fulfilled (Octet Rule).
Regarding the coordination compounds, Lewis postulated that: «the groups that are attached to the metal ion, forming the coordination entity, have lone pairs of electrons, that is, they are not shared in a bond ” and defined the coordination number as “the actual number of pairs of electrons that are attached to the metal atom”.
In another aspect of his theory, Lewis proposed a more general definition for acids and bases, in which a base is one that has a lone pair of electrons that it can donate to another atom, while an acid is the substance that It can accept a lone pair of electrons to form a bond. In this sense, the metal ion in a complex is a Lewis acid and the groups that are attached to this ion in the coordination entity are Lewis bases.
Lewis proposed his model in 1916 and Sidgwick extended it around 1927, and it turned out to be a true revolution in chemistry because it made it possible to explain in a simple way the nature of the chemical bond in extremely diverse compounds, coming, for example, to consider from this point of view, all complex chemistry as simple acid-base reactions.
The Lewis model was later extended and completed by the Valence Bond Theory (TEV) and the Molecular Orbital Theory (TOM) that currently allow us to interpret the vast majority of reactions and properties of complexes.
Nature of the core group-ligand binding
Usually ligands are nucleophiles, anions, polar or easily polarizable molecules that possess at least one unshared valence pair of electrons, such as H
2O, NH
3, X−
, RCN−
, etc.
This initially leads to trying to explain in a simple way the attractions that are established between ligands and cations as electrostatic in nature: the pair of electrons of the ligand is intensely attracted by the high charge of the cation, forcing the molecule or anion that owns to approach.
However, this approach does not allow us to explain how complexes with central neutral or negatively charged groups are formed.
A better approximation is to consider the central group-ligand union as a particular type of Lewis adduct in which the electrons of the ligand's unshared electron pair and the empty orbitals (either atomic or molecular) of the central group participate. In this bond, the ligand contributes a pair of unshared valence electrons (Lewis base), and the central group accepts them (Lewis acid) to form one of the covalent bonds of the complex.
The union established between the central group and the ligand is therefore covalent.
This type of covalent bond, in which one of the atoms contributes the two bonding electrons, is called a coordinate covalent bond.
Based on this model, some authors make a difference between the covalent bond itself, where it is assumed that each committed atom contributes an electron to form the bond by electron pair, and the coordination bond, where it is proposed that only one of the committed atoms in the bond contributes the pair of electrons. Although this differentiation helps to understand the origin of the bond, once the coordination compound is formed it no longer makes sense, since the bonds are equivalent.
The simplest example to illustrate the above is the H
3N and the H
3N-H+
or better NH+
4, where you might think that This last link is different because it is coordinated and in some texts it even reached a to be represented as H
3N→H+
; however, the NH+
4 is a regular tetrahedron, in which each of the four links is equivalent to the others and therefore impossible to differentiate.
The ease with which this covalent bond is formed is explained in a simple way by the ability of the central group to deform the cloud of electrons of the ligand, this ability is all the greater the greater the charge/radius ratio thereof.
This allows us to deduce why cations, and especially those with greater charge and smaller size, are the ones that form complexes more easily.
This last rule has, however, some deviations: for example chrome Cr3+
that has an ionic radius of 0.62 Å forms complexes more easily than aluminum Al3+
, which has a ionic radius of 0.45 Å. In these cases, it is worth considering the impediment that certain anions or large molecules have to get close enough to form the bond with the empty orbitals of the central group.
The possibility of a bond being formed between the ligand and the central group is conditioned, firstly, by the existence or not of empty orbitals in the central group, and secondly, by the spatial interference that they cause among themselves. ligand molecules trying to access the positions where it would be possible for the bond to form; this is known as steric hindrance. One can get a pretty good idea of steric hindrance by imagining a bunch of pigs trying to access a bowl that is too small.
It is largely for this reason that coordination chemistry is dominated by transition and internal transition metals, since these are atoms capable of acquiring high charge/radius ratios, generally possessing a large number of orbitals unoccupied valence orbitals (d orbitals in transition metals and f orbitals in inner transition metals), and that even so have a radius large enough to allow the approach of a large number of ligands.
Ligands
Anions or molecules capable of acting as ligands must have atoms that have at least one pair of unshared valence electrons. These atoms are found in the upper right corner of the periodic table, and among them the most important are oxygen and nitrogen, later giving way to carbon, phosphorus, sulfur, chlorine, fluorine, etc.
Molecules that have a single electron donor atom are called monodentate ligands, while those that have more than one donor atom are called polydentate ligands or agents. chelators. There is also a third type of ligands known generically as ambidentate ligands which are actually ligands that act as monodentates, but in two different ways.
Monodentate ligands
Ligands of this type have a single anchor point to the coordination nucleus, hence the name monodentate, which means a single tooth. Usually these are small molecules, which have a single electron donor atom, such as ammonia (NH
3), water (H
2O), or halide anions (X−
), alkoxide (RO−
), or I rent (R−
) among others.
When a complex of a metal cation is formed from the union with monodentate ligands, the solubility properties of the cation are notoriously altered, in general this is due to the fact that the complexation causes an increase in the size of the ion, which in turn In turn, it translates into a decrease in the attractive force between the cation and its counterions. This usually causes an increase in the solubility of the ion, or, better expressed, a decrease in its tendency to precipitate.
Polydentate ligands or chelating agents
Ligands of this type are capable of establishing two or more simultaneous unions with the coordination nucleus, they can be bidentate, tridentate, tetradentate > etc These types of ligands are also often called "chelating agents" a name derived from the Greek word kela meaning "clamp" because the kind of spatial structure that is formed resembles a crab with the coordinating nucleus caught in its claws. Chelating agents are often used as precipitating agents, since by being able to establish two or more simultaneous unions they can also function as "bridges" between two or more coordination nuclei, facilitating the formation of enormous macromolecular aggregates that precipitate easily.
Among this type of compound we find, for example, phosphate anions (PO3−
4), carbonate (CO2−
3), oxalate (-OOC-COO-), ethylenediamine (NH
2-CH
2-CH
2-NH
2) and bipyridine. A polydentate ligand of enormous importance due to the number of applications it has is EDTA, EDTA has six binding sites.
Ambidentate ligands
This type of ligands could be considered a special case of polydentate ligands, because they have more than one atom capable of donating unshared pairs of electrons, however they are too small in size to be able to donate electrons with both atoms to at the same time, and instead they are linked in one way or another depending on the circumstances.
Within this group we find, for example, the anions thiocyanate (S=C=N-), nitrite (O=N-O-) and isothiocyanate (NC-S-)
Cargo and coordination number
The total charge of a complex ion is determined by the sum of the charges of the coordination nucleus, plus that of the ligands that participate; for example in the hexacyanoferrate(III) ion [Fe(CN)
6]3-, the load of the cation is +3, and each of the cyanide ions has charge -1, so:
Q=6⋅ ⋅ (− − 1)+3=− − 3{displaystyle Q=6cdot (-1)+3=-3,}
which is the total charge of the ion.
The ligands bind to the coordination nucleus in a region quite close to it called the coordination sphere, which is the place in space where it is possible for the electrons of the ligand to interact with the empty orbitals of the central group.
Each of the ligand atoms that enters the coordination sphere to contribute a pair of unshared electrons is called a donor atom.
The coordination number of a coordination nucleus is directly the number of pairs of electrons it receives from the atoms of the ligand(s). This value depends on the size of the coordination nucleus and the size of the ligands that participate in the complex. For example iron Fe3+
coordinates with up to 6 fluoride anions to form the [Fe(F)
6]3−
(coordination number = 6), but only can coordinate with up to 4 chloride ions [Fe(Cl)
4]−
(coordination number = 4) due to the larger size of the latter.
Formulation and nomenclature
Rules of formulation
To express the formula of coordination compounds, it is convenient to keep in mind the formulation rules recommended by IUPAC, these rules are:
- The complexes are written in square brackets
- In the brackets the cationes are written first, then the anions and finally the neutral species.
- If there are two or more species with the same type of load, they are alphabetically ordered according to the atom that is attached to the central atom.
- Finally and outside the brackets, it is written as superscript the total load of the complex. Thus for example the hypothetical complex formed by 1Co3+
3NH
3 1H
2O, 1Cl−
1F−
would be correctly typed as: [CoClF(NH)
3)
3(H
2O)]+
Nomenclature rules
Regarding the nomenclature IUPAC recommends:
- To be present in the first place if it is an anionic complex (with negative load) cationic (with positive load) or if it is a neutral species. For example:
- [CrCl(NH)
3)
5]2+
It is a Catholic complex. - [Co(CN)
6]4−
It's an annionic complex. - [CuBr
2(NH
3)
2] It's a neutral complex.
- [CrCl(NH)
- In naming it the ligands are first quoted, and these in alphabetical order.
- Anionic ligands are cited by their usual name, for example H- (hydruro) or ClO−
4 (perchlorate). Although there are a certain number of ligands with special names, whereas for neutral ligands its usual name is used, with two exceptions:
| ♪ | Name | Type |
| F− | fluoride | Aniónico |
| Cl− | chlorine | Aniónico |
| Br− | bro. | Aniónico |
| I− | I am. | Aniónico |
| O− 2 | ox | Aniónico |
| OH− | hydroxo | Aniónico |
| O2− 2 | Peroxo | Aniónico |
| HS− | mercapto | Aniónico |
| S− 2 | Uncle | Aniónico |
| H 2O | Aqua | Neutral |
| NH 3 | Ammin | Neutral |
| NO | Nitrosilo | Neutral |
| CO | Cabonilo | Neutral |
- Alphabetical order does not consider numerical prefixes that indicate the presence of several molecules of the same ligand. For example aqua, diaqua and triaqua go before ciano.
- The di-, tri-, etc. prefixes are used to specify the number of each simple ligand class (unidentified).
- For complicated ligands (polidentated flare agents), other prefixes are used:
| Number of ligands | Prefix |
| 2 | bis |
| 3 | tris |
| 4 | Tetraquis |
| 5 | Pentaquis |
| 6 | hexaquis |
- The name of complicated ligands is written in brackets.
- The ambitious ligands receive a different name according to what the atom is attached to the central group. For example:
- NO
2 if it binds through oxygen (subject:O-NO) is called nitrite, but if it does so through nitrogen (i.e.:NO
2) is called nitro. - SCN if it joins through sulfur (-S-CN) is called thiocyanate, but if it unites through nitrogen (-NCS) it is called isotyocyanate.
- NO
- Once all the ligands have been named, the central atom is named as follows:
- If it is an ANIONIC complex the root of the name of the central atom followed by the ATO termination is used, and in the end between parentheses is written the state of oxidation of the central atom with Roman numerals (Stock System). For example:
- [Fe(CN)
5(H
2O)]2−
: ion aquapentacianoferrato (III)
- [Fe(CN)
- If it is a CATIONICO or NEUTRO complex, no suffix is added to the name of the central atom. For example:
- [Ni(CO)
4] tetracarbonylnique (0) - [Fe(H)
2O)
6]2+
ion hexaaquahierro (II)
- [Ni(CO)
- Complex ion salts are called any other salt, taking into account the name of the complex anion or cation. For example:
- K
4[Fe(CN)
6] hexacianoferrato (II) of potassium - Mg
2[Ni(NCS)
6] nickelate (II) hexakis of magnesium - [Co(H)
2O)
6]Cl
2 hexaaquacobalto (II) chloride - [Cu(NH)
3)
4THAT
4 tetrammincopper sulfate(II) - [CoBr
2(in)
2]Cl dibromobis chloride (ethylenediamine) cobalt(III) - [Pt(NH)
3)
4][PtCl
6] hexachloroplate(IV) of tetramminplatin(II)
- K
Metal complexes
Virtually all metal compounds are formed by some kind of coordination compound (with the exception of metals in the vapor state, plasmas, and alloys). So the study of coordination chemistry is largely equivalent to the study of inorganic chemistry, since coordination chemistry is the chemistry of most of the periodic table. Metal atoms and ions only exist in the condensed phase surrounded by ligands.
Areas of metal coordination chemistry can be classified according to the nature of their ligands. Broadly speaking, these divisions are:
- Classical coordination chemistry (or the "Werner Complex"): here the ligands join the metals, almost exclusively, by means of solo pairs of electrons that come from the main group of ligand atoms. Examples: H2O, NH3, Cl-, CN-, en-, [Co(EDTA)]−[Co(NH]3)6]Cl3, Fe(C2O4)3]K3
- Organometallic chemistry: ligands are simple organic compounds (alchenos, alkynos, alkylos) as well as ligands of structure similar to organics such as phosphine, hydrogen and carbonyl. Example: (C5H5)Fe(CO)2CH3
- Bioinorganic chemistry: ligands are organic compounds produced by living beings, especially lateral chains of amino acids, and many cofactors such as porphyrins. Examples: Hemoglobin, Vitamin B12, Clorofila
- Chemistry of clusters (groups), in this the ligands are all mentioned above and also includes other metals as ligands. [Rule]3(CO)12]
Although in many cases it is difficult to classify a case within a particular group and it is easier to interpret it as a combination of several of them. Examples: [Fe4S4(Cysteinil)4]2−, which is actually a contained cluster inside a biologically active protein.
Mineralogy, materials technology, and solid-state chemistry (as applied to metal ions); they can be considered subdivisions of coordination chemistry, in the sense of considering metals surrounded by ligands. In many cases these ligands are oxides or sulfides. It is true that the focus of mineralogy, materials technology, and solid-state chemistry differs from the usual focus of coordination chemistry. The former are concerned primarily with polymeric structures, and with the properties that derive from the collective effects of a huge number of interconnected metals. While the second, in contrast, focuses on the reactivity and properties of complexes containing individual metal atoms, or small clusters of atoms; but even so, the metals are coordinated, and the guidelines and principles considered for complexes also apply to them.
Spatial structure of complexes
Molecular structures in coordination chemistry are mainly described by the coordination number, that is, by the number of ligands attached to the central group (more specifically, the number of sigma bonds between ligands and central group). It is usually possible to count the bound ligands, but sometimes the ligand count can become a bit ambiguous. The coordination number is normally between one and nine, but even higher coordination numbers are not uncommon for the lanthanides and actinides. The coordination number will depend on the size, charge, and electronic configuration of the central group and the ligands.
Metal ions can have more than one coordination number.
The chemistry of complexes is dominated by the interactions between the s and p molecular orbitals of the ligand and the d orbitals of a central metal ion. Together the s, p, and d orbitals of the central ion can accommodate 18 electrons (see the 18-electron rule), although for f-block elements, this rule extends to 32 electrons. The maximum coordination number for a certain element is therefore related to its electronic configuration, (more specifically with the number of empty orbitals it has), and to the relationship between the size of the ligands and the size of the central group. Large core groups and small ligands allow for high coordination numbers, for example [Mo(CN)8]4-. Small core groups and large ligands tend to develop small coordination numbers, for example Pt[P(CMe3]2. It is precisely because of their large size that lanthanides, actinides, and first transition elements tend to develop high coordination numbers.
Different coordination numbers result in different structural arrangements. Most of the structures follow a quasispherical pattern (or, seen in another way, as if the central group were in the middle of a polyhedron and the ligand groups were located at the vertices of it). It is at these points that overlap between the ligand orbitals and the central group is possible. Ligand-ligand repulsions tend to direct this organization towards certain regular geometries that minimize interference. There are, however, numerous cases of deviations from these regular organizations, for example in cases where ligands of different types bind, causing different bond lengths, moving the ligands away from their quasispherical organization, or when distortions occur due to electronics, for example in the Jahn-Teller distortion.
Geometry
For coordination numbers between two and nine the most common geometric arrangements that occur in complexes are those that tend to minimize the repulsion forces between valence shell orbitals
However, some exceptions and provisions should be noted:
- The idealized description for coordination numbers 5, 7, 8 and 9, is often geometrically indistinct of alternative structures with slightly different L-G-L angles (light-Central-Landing Group). The classic example of this is the difference between square pyramidal structures and trigonal bipiramidal.
- Due to some special electronic effects, such as the stabilization of second order Jahn-Teller, certain geometries are favoured against other possible structures. For example, for some compounds with coordination number six, the prismatic wheat geometry is favored by stabilization and is the one adopted by the complex instead of the octahédrica.
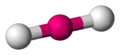
Linear
The Linear is the lowest energy structure for a coordination number two. In this arrangement the central group is between the two ligand groups and all three form a line with a bond angle L-G-L of 180º.
Flat Trigonal
The trigonal planar molecular geometry is the structure that minimizes interactions for a coordination number of three. In this arrangement, the central group is located in the center of an equilateral triangle and the ligand groups are located at its vertices, with a bond angle L-G-L of 120º.
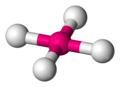
Tetrahedral
The tetrahedral structure is the one with the lowest possible energy for a coordination number of four. In this arrangement, the central group is in the middle of a regular tetrahedron and the ligand groups are located at the vertices of the tetrahedron with a bond angle L-G-L of 109.5º.
Square plane
The square plane molecular geometry is another possible structure for a coordination number four, in which the four ligands are arranged in the same plane at the vertices of a square. It is apparently of higher energy than the tetrahedral since the angles L-G-L are 90º, but here repulsions due to orbitals with lone pairs that are in the polar positions (the pairs are in a plane perpendicular to the plane shared by the molecules in arrangement) participate. square). Metals with electron configuration nd8 tend to adopt the square planar geometry.
Trigonal Bipyramidal
The trigonal bipyramidal molecular geometry is the one that maximizes the separation angles, and therefore minimizes the energy for a coordination number of five. it can be seen as two tetrahedrons joined at the base and is very close in energy to its isocoordinate. This arrangement is anisotropic, the ligands in the equatorial position are separated by 120º from each other, but an equatorial ligand is separated by 90º from a polar one.
Square pyramid
The square pyramidal molecular geometry is obtained by slightly displacing one of the polar vertices of a trigonal dipyramid until leaving it in the same plane as the one formed by two of the equatorial vertices and the remaining polar vertex.
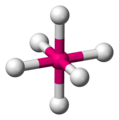
Octahedral
The octahedral is the most typical geometric arrangement for transition elements, and it is not hard to see why, if we put a sphere inside a cube (inscribed sphere), the sphere would touch the faces of the cube at the vertices of an octahedron. This arrangement consists of four ligands placed in the same plane (called the equatorial plane) and one ligand on each side of that plane in "polar position". In this structure, the minimum angle between ligands is 90º..
Trigonal prismatic
The trigonal prismatic molecular geometry is the next most stable for a coordination number of six, it is usually less stable because it implies that the ligands of the vertices of the prism face each other, this interference is minimized in the octahedral arrangement (which in a certain way could be considered a trigonal antiprism, where the upper face has been rotated so that the vertices are not facing each other). In general, this structure is presented by a stabilization due to some other not exclusively geometric factor, for example by forced distortion of orbitals.
Pentagonal bipyramidal
The pentagonal bipyramidal configuration is preferred for a coordination number seven, as its name implies it can be seen as two pentagonal-based pyramids joined at the base.
Square antiprismatic
The square antiprismatic molecular geometry is the configuration with the lowest energy among the three possible configurations for a coordination number eight, it can be thought of as a cube in which the upper face has been rotated so that the vertices do not face each other.
Hexagonal bipyramidal
The hexagonal bipyramidal molecular structure is the next most stable for a coordination number of eight.
Treaped tetrahedral
The triapic tetrahedral molecular structure is a very strange structure among transition metals, but for internal transition elements it turns out to be the structure that minimizes all ligand interactions and orbital distortions so it occurs even in very simple compounds such as ThCl4. It can be rationalized as a dodecahedron with triangular faces.
Cubic
It is the least geometrically stable of the configurations for coordination number eight and is virtually non-existent for transition elements, although it appears to be quite common among inner transition elements, mainly because the f(xyz) orbitals point towards the vertices of a cube, which decreases the distortion of these orbitals when interacting with the ligands.
Triapicated trigonal prismatic
The trigonal tripicate prismatic is the most regular and stable geometry that exists for a coordination number nine. The easiest approximation to understand this three-dimensional structure is to imagine a trigonal prism and at half height insert a triangle so that its vertices are pointing to the center of the square faces of the prism.
Coordination indices greater than 9
Although more than two thirds of the known complexes have coordination indices between 6 and 9, some examples of lanthanides and actinides with higher coordination indices are known: 10, 11 or 12.
Coordination number 12 presents a greater number of examples than coordination number 10 and very few have been described for coordination number 11. However, it should be mentioned that, in all cases, they are complexes that involve chelate ligands or macrocycle, there are no known examples of complexes with coordination indices greater than 9 formed by monodentate ligands.
For a coordination number 12, one would expect a regular icosahedral-shaped structure. However, this structure practically does not exist in practical chemistry. On the contrary, the vast majority of the structures described correspond to truncated tetrahedrons, cubooctahedrons, or tetraapic cubes.
There are works in computational chemistry that conclude that in reality the best way to reflect coordination indices greater than 9 for these structures is through simpler bonding schemes (tetrahedron, trigonal dipyramid or octahedron) and that the pseudoregular structures observed are actually a consequence of the interaction of the chelate ligand orbitals with the large surface area of the central group 4f, 5f, 5d or 6d orbitals, and not only due to coordination with the donor atoms.
Geometric Gallery
Isomerism
Isomerism is the property that relates two or more compounds that have the same type and number of atoms, but are structurally organized in a different way.
For reasons of clarity it has been placed in a different section, although technically it falls within the study of complex geometry.
The structural organization of a certain complex is, in general, fixed and stable, and is determined by the arrangement with the lowest possible energy, (this is more or less equivalent to saying that it adopts the arrangement with the lowest internal stresses), however, in some of these cases there is more than one architecture with equivalent or very similar energies, which allows the components of that complex to adopt more than one structural layout. In such cases isomerism of complexes occurs.
There is a great variety of types of isomerism in coordination complexes, only comparable in complexity by the isomerism of carbon compounds.
Stereoisomerism
Stereoisomerism is the type of isomerism that occurs when in two compounds there are not only the same type and number of atoms; but also the same type and number of links, but spatially arranged differently.
Stereoisomerism can be classified as:
Geometric isomerism
Geometric isomerism occurs in octahedral complexes and flat squares (not in tetrahedral ones). When two ligands They occupy different relative positions with respect to each other. Thus, when two ligands are opposite each other, they are said to be trans and when they are mutually adjacent, they are said to be cis. When three identical ligands occupy one of the faces of an octahedral arrangement, it is said to be a facial or fac isomer. If all three ligands lie in the same plane as the central group, the isomer is said to be meridional or mer.
For example, in an octahedral compound with three ligands of one type and three ligands of another, there are two geometric isomers: the mer in which each of the two groups of three ligands is found on one of the meridians, and the fac in which each group of three ligands is found on one of the faces of the octahedron.
Optical isomerism
Optical isomerism occurs when the mirror image of a compound is not superimposable with the original compound. It is called optical isomerism because the compounds are optically active, that is, they rotate the plane of vibration of polarized light. This uneven behavior occurs because the bonds, which are nothing more than groups of electrons, resonate differently when subjected to the electromagnetic field that is light. In optically active compounds the sum of all the resonances results in different vectors, because the bonds certainly have different orientations.
the symbol Λ (lambda) is used to describe the left-handed helix made up of three bidentate ligands, as shown. Similarly, the symbol Δ (delta) is used as a prefix to describe the right-handed helix.
Structural isomerism
This type of isomerism occurs when the number and type of atoms are the same, but bonds are different from each other. There are two main types of structural isomerism in coordination compounds, bond isomerism, which occurs when the ligands accessing the coordination sphere are the same, and coordination sphere isomerism, in which the ligands in the coordination sphere of coordination are different.
Bond Isomerism
Bonding isomerism occurs when a ligand can be attached to the central group in more than one way, a clear example is what happens with ambidentate ligands, for example NO2 is a Ambidentate ligand: it can be attached to the central group by any of its oxygens (which are equivalent) or by nitrogen.
Coordination sphere isomerism
This type of isomerism occurs when a coordination compound alternates the ligand groups that access its coordination sphere by groups that are outside it in the solid lattice (see water of crystallization). For example, CrCl3(H2O)6 exists in three common forms: [Cr(H2O)6]Cl3 (purple), [Cr(H2O)5Cl ]Cl2H2O (green), and [Cr(H2O)4 Cl2]Cl 2H2O (also green). In the second and third compounds, the water has been displaced from the coordination sphere by chloride ions and instead has occupied positions in the solid lattice of the crystal.
Electronic structure of complexes
Virtually all the properties that are observed in the complexes are the product of their electronic structures, that is, they are functions of the way in which the electrons are organized within the molecule, trying to understand how these electrons are found organized is a good way to try to begin to understand the properties of complexes.
From Werner's discoveries, different theoretical models began to appear that tried to explain the strange behaviors observed in the complexes.
Around 1929, the theory of the crystalline field (TCC) appeared, proposed by the physicists Hans Bethe and Van Vleck, which makes it possible to explain the color and magnetic properties of complexes in a very simple conceptual way, although it does not correlate well with all the complexes, nor does it allow us to explain the nature of the links.
Around 1933 Linus Pauling introduces the valence bond theory (VTE), which tries to explain the reason for the directionality of bonds in compounds and begins to give an explanation of their nature.
Molecular orbital theory (MOT) is a natural consequence of valence bond theory that advances the quantum aspects of chemical bonding, allows a much deeper understanding of the phenomena involved in the formation of a chemical bond and It allows to explain the behavior of many classes of complexes, however for many applications it is too complicated.
Ligand field theory (LFT) is a combined model that allows a simple derivation of molecular orbital theory, using an application of group theory to solve the formal equations. It enjoys almost the same conceptual simplicity as crystal field theory and allows a large number of compounds to be explained reasonably accurately.
In all scientific disciplines, it is always a question of using the simplest model that serves to explain each particular situation, which is why, despite the fact that the molecular orbital theory is the one that provides a more realistic simulation, in In general, for simple situations, crystal field theory is often used as a model.
Crystal Field Theory (CFT)
This theory considers only the geometry of the d orbitals of a central cation and its interaction with some ligands considered as punctual negative charges. According to this model, the ligands are attracted by the positive charge of the metal, but when approaching they generate repulsions on the d electrons of the cation, deforming the orbitals in which they are found. A deformed orbital has a higher energy than one with its "natural" so the electrons tend to occupy positions in the "native" whenever possible, this is provided that the energy difference between the higher and lower energy orbitals is not less than the pairing energy due to the repulsion of electrons in the same orbital.
A simple example is what happens for an octahedral complex, if it is assumed that the ligands move along the axes of a three-dimensional Cartesian system, the orbitals that are going to be mainly affected are those with principal components on these axes. When looking at the graph of d orbitals, you can see that these orbitals are d z2 and dx2-y2. As a consequence, they increase their energy and separate from the rest of the d orbitals, forming two subgroups of orbitals: the high-energy group eg and the low-energy group t2g.
The degree of separation between eg and t2g orbitals will depend on the strength of the ligands, that is, on the degree to which these ligands are capable of deforming the d orbitals. The spectrochemical series is an empirical table that orders the ligands according to the degree of separation they cause in the d orbitals, from lowest to highest strength they are:
I− < Br− < S2− < SCN− < Cl− < NO3− < N3- < F− < OH− < C2O42− < H2O < NCS− < CH3CN < py < NH3 < in < 2,2'-bipyridine < phen < NO2− < PPh3 < CN− < CO
According to this model, the electronic transitions between these d orbitals of different energy are responsible for the absorptions of certain wavelengths that give color to the complexes (the shorter the wavelength, the higher the energy and therefore the greater the strength of the ligand).
When the separation between low-energy and high-energy orbitals is greater than the pairing energy of the electrons, all the electrons tend to occupy positions in the low-energy orbitals according to the Aufbau principle, forming what is called known as a low spin complex. On the other hand, if the separation between orbitals is smaller than the pairing energy, the electrons tend to occupy all the orbitals (whether low or high energy) before starting to pair according to Hund's rule, forming what is known as a high spin complex.
According to this model, the number of electrons under paired or unpaired spin conditions are responsible for the magnetic properties of the complexes.
Valence Bond Theory (VTE)
Valence bond theory is primarily a geometric advance on a Lewis structure. Basically it is based on the idea that several different atomic orbitals can be combined in a linear way (that is, following the operations of linear algebra) to form hybrid orbitals of equal energies and with a particular arrangement in space.
Linus Pauling, using the ideas of a previous work by Walter Heitler and Fritz London, developed between 1930 and 1940 this new theory on the covalent bond saying that it is formed by overlapping or superposition of two atomic orbitals, so that the shared electrons belong to the orbitals of the two bonded elements at the same time. In other words, this theory assumes that the formation of the covalent bond occurs because the overlapping or overlapping of the atomic orbitals of the participating atoms occurs, and that this pairing occurs in such a way that the pairing of electrons with electronic spins of opposite sign; giving rise to a spatial region of increased electron density common to both atoms.
In a few words, this theory establishes that a chemical bond is formed when orbitals of different atoms are combined in a linear way in certain regions of space, however it differs from the theory of molecular orbitals in that the valence bond theory considers electrons as belonging to each particular atom.
To understand it, it is necessary to take into account that only the outermost orbitals of the atomic structure will be of interest, and that those hybridization structures that maximize the interactions to form bonds are favored in the spatial form they acquire, that is, that they increase the overlap or overlap of orbitals.
The theory of the valence bond is part of and complements the theory of molecular orbitals. Molecular orbital theory can predict magnetic properties (diamagnetism and paramagnetism) in a more direct way, although valence bond theory in a complicated way generates the same results.
Molecular Orbital Theory (TOM)
The theory of molecular orbitals makes use of a linear algebraic combination of wave functions of atomic orbitals to form hybrid orbitals, in this sense it is similar to the valence bond theory, with the difference that the theory of molecular orbitals considers that the atomic valence orbitals disappear when a compound is formed, leaving in their place molecular orbitals that cover the entire molecule. A molecular orbital is nothing more than a Schrödinger orbital that includes more than one atomic nucleus in its formulation.
The theory of molecular orbitals indicates that as many molecular orbitals are formed as there are valence atomic orbitals available to form them. Thus, if it is a compound that has two atoms, one with an s orbital and the other with an s orbital and three p orbitals, the molecule formed will have five molecular orbitals.
These molecular orbitals are divided into bonding, nonbonding, and antibonding. Bonding orbitals are those in which electrons tend to spend most of their time forming a zone of high charge density between atomic nuclei, this zone causes attractive nucleus-electron-nucleus interactions that hold atoms together. A non-bonding orbital is very similar to an atomic orbital (in the linear combination it has a higher proportion of atomic orbital than molecular orbital), and it is located in deep layers of the molecule, an electron in this type of orbital tends to pass approximately the same time near each nucleus without generating a true charge density between the two, so that the attractive forces nucleus-electrons-nucleus are approximately of the same magnitude as those of repulsion between nuclei. An antibonding orbital is one in which the electrons spend most of their time away from the nuclei, so the nucleus-nucleus repulsions that occur are much greater than the nucleus-electrons-nucleus attractions.
The electrons provided by each participating atom are distributed within the molecular orbitals according to Hund's rule, if there are many electrons in bonding orbitals the compound has a high tendency to form and is very stable, and if there are the same number of electrons in bonding orbitals than in non-bonding orbitals the compound is not formed.
The theory of molecular orbitals arrives at results similar to those of the hybridization of atomic orbitals described by the valence bond theory, to describe the geometry of molecules and among them the geometry of complexes, also allows to predict very accurately chemical reactivity, magnetic properties, color and even electrical conductivity of different substances. It is very useful for computational modeling of molecules, especially extremely large molecules, and is very easy to understand for an approach with a small number of atoms. In a certain way, the valence bond theory can be considered a kind of limiting case of the theory of molecular orbitals. However, their solutions are too complex to solve on paper from a relatively small number of atoms. (As an example, according to this theory, a complex with a central atom of the d block, and five ligands of the p block, has 29 molecular orbitals, and this is considering monatomic ligands), so it is often easier to use the TEV.
Binding Field Theory (TCL)
The theory of the field of ligands that in a certain way can be considered a hybrid between the theory of molecular orbitals and the theory of the crystalline field; actually represents a group-theoretic application of molecular orbital theory. It allows to describe the bond, the geometric arrangement of orbitals, the magnetic characteristics and the colors of the coordination compounds without the limitations that the CBT presents and with fewer difficulties than the TEV.
The TCL analysis is very similar to that done by molecular orbitals, but it is highly dependent on the geometry of the complex, since it only makes use of the orbitals that "geometrically speaking" they can form bonds, to combine them in molecular orbitals. This considerably simplifies the approaches and results and allows valid conclusions to be reached without having to resort to the use of complicated computational models.
Staining of the complexes
A substance has color when it absorbs certain electromagnetic wavelengths within the visible range.
The absorption of certain wavelengths is due to the transition between two energetic states of the electrons that form the orbitals of an atom, or the bonds of a molecule.
Each type of electron can absorb only certain amounts of energy, due to the nature of the atomic or molecular orbital it occupies.
Since the difference in energy between two electronic levels is equal to the energy of the absorbed photon, it is possible to relate this energy to the wavelength of the photon according to:
E=h.. {displaystyle E=hnu ,}
or what is the same:
E=hcλ λ {displaystyle E={frac {hc}{lambda }},}
Where:
- E{displaystyle E} is the energy
- h{displaystyle h} is the constant of Planck
- .. {displaystyle nu } is the frequency of the wave
- c{displaystyle c} is the speed of light
- λ λ {displaystyle lambda } is the wavelength
Then each electronic transition absorbs certain wavelengths of light. If the transition absorbs wavelengths within the visible range (420 to 750 nm), then the compound, when illuminated with white light, appears colored; and precisely the complementary color to the absorbed color. For example, a compound that absorbs red light will show a color composed of the colors blue and green that are not absorbed, one that absorbs green will show violet (red and blue), one that absorbs blue will show yellow (green and red)., etc.
The remarkably bright and vivid colors of coordination compounds are determined by the difference in energy (D) between the eg and t2g orbital sets in their ions complexes. When the ion absorbs light in the visible range, electrons are excited (jump) from the lower energy level t2g to the higher energy level eg.
For example, consider the ion [Ti(H2O)6]3+, which gives rise to purple solutions in water. The hydrated Ti3+ ion is a d1 ion, with the d electron in one of the three lowest energy t2g orbitals. The difference in energy (D) between the eg and t2g orbitals in this ion corresponds to the energy of the photons spanning the green and yellow range. When white light falls on the solution, these colors of light are absorbed, and the electron jumps into one of the eg orbitals. Red, blue, and violet light is transmitted, so the solution appears purple.
Absorption spectra show the wavelengths absorbed by a metal ion with different ligands, and by different metal ions with the same ligand.
From data like these, it is possible to infer the structure of the d orbitals that take part in the complex since we relate the energy of the light absorbed with the values of D (energy difference between high and low spin orbitals) Two important observations emerge:
For a given ligand, the color depends on the oxidation state of the metal ion. A solution of the ion [V(H2O)6]2+ is violet, and a solution of the ion [V(H2O)6]3+ is yellow. For a given metal ion, the color depends on the ligand. This observation allows classifying the ligands in the spectrochemical series mentioned above.
| FeII | FeIII | CoII | CuII | AlIII | CrIII | |
|---|---|---|---|---|---|---|
| Ion moisturized | [Fe(H)2O)6]2+ Pale green Soluble | [Fe(H)2O)6]3+ Yellow/brown Soluble | [Co(H)2O)6]2+ Pink Soluble | [Cu(H)2O)6]2+ Blue Soluble | [Al(H)2O)6]3+ Colorless Soluble | [Cr(H2O)6]3+ Green Soluble |
| OH-diluted | [Fe(H)2O)4(OH)2] Dark green Precipitated form | [Fe(H)2O)3(OH)3] Brown Precipitated form | [Co(H)2O)4(OH)2] Blue green Precipitated form | [Cu(H)2O)4(OH)2] Blue Precipitated form | [Al(H)2O)3(OH)3] White Precipitated form | [Cr(H2O)3(OH)3] Green Precipitated form |
| OH-, concentrated | [Fe(H)2O)4(OH)2] Dark green Precipitated form | [Fe(H)2O)3(OH)3] Brown Precipitated form | [Co(H)2O)4(OH)2] Blue green Precipitated form | [Cu(H)2O)4(OH)2] Blue Precipitated form | [Al(OH)4]- Colorless Soluble | [Cr(OH)6]3– Green Soluble |
| NH3diluted | [Fe(H)2O)4(OH)2] Dark green Precipitated form | [Fe(H)2O)3(OH)3] Brown Precipitated form | [Co(H)2O)4(OH)2] Blue green Precipitated form | [Cu(H)2O)4(OH)2] Blue Precipitated form | [Al(H)2O)3(OH)3] White Precipitated form | [Cr(H2O)3(OH)3] Green Precipitated form |
| NH3, concentrated | {[Fe(H)2O)4(OH)2] Dark green Precipitated form | [Fe(H)2O)3(OH)3] Brown Precipitated form | [Co(NH)3)6]2+ Pajizo Soluble | [Cu(NH)3)4(H2O)2]2+ Intense blue Soluble | [Al(H)2O)3(OH)3] White Precipitated form | [Cr(NH)3)6]3+ Green Soluble |
| CO32– | FeCO3 Dark green Precipitated form | [Fe(H)2O)3(OH)3] Brown Precipitated form Releases CO bubbles2 | CoCO3 Pink Precipitated form | CuCO3 Blue green Precipitated form |
Magnetic properties of complexes
In general, the magnetic properties depend on the number of unpaired electrons that the complex possesses. When there are one or more unpaired electrons, the complex is paramagnetic and will be attracted to magnetic fields proportional to the number of unpaired electrons. If there are no unpaired electrons, the compound will be diamagnetic and will be slightly repelled by magnetic fields. Since being unpaired, the energy of the system is lower, if the energy splitting is small, the situation in which the electrons are unpaired is more favorable, occupying the upper and lower d orbitals (high spin configuration) while if the splitting is large, the electrons will be paired in the lower d levels (low spin configuration). In the first case, the complex is strongly paramagnetic, while in the second it is only weakly so (5 e-unpaired vs. 1).
Chemical properties of the complexes
Complexes can present a wide variety of chemical properties depending on the type of reaction in which they participate:
- Electron transfer reactions
- The most common types of electron transfer reactions in which the complexes are involved are two: electron transfer within the sphere of electron coordination and transfer with the outside of the focal area. Within these types of reactions the transfer of electrons occurs by classic redox mechanisms, or by means of a ligand bridge, in which a ligand with two solo pairs is attached to two different focal points, the electrons are transferred from one of the focal points to the other through the ligand.
- Link Exchange Reactions (degenerate)
- An important indicator of the reactivity of a complex is the exchange rate between degenerate ligands (iguales). For example, the exchange rate among the water molecules involved in type complexes [M(H)2O)6]n+, varies in more than 20 orders of magnitude between the most stable and the most unstable complexes. Those complexes in which the ligands are released and reconnected very quickly are classified as weak. Such labil complexes can be very unstable thermodynamically. A typical labil metal complex has a low load (e.g. Na+), electrons in orbital d that are anti-linking with respect to ligands (Zn2+), or a low degree of covalent character in the link (Ln3+where Ln is any lanthanid. The instability or lability of a metal complex also depends on the type of electronic configuration it presents. For example, the high-spin complexes of Faith(II) and Co(III) are weak, while the similar low-spin complexes are inert. The Cr (III) may exist only in a state of low spin (quartet), which is inert due to the absence of electrons in orbitals that are anti-linking in the Metal-Ligar ratio, plus some stabilization due to the ligand field associated with the d configuration3.
- Associative processes
- The complexes that have empty or semi-filled orbitals also present the ability to react with other substrates. Most of the substrates have a single basal state; this is that they have lone pairs (e.g. water, amines, ethers), so that such substrates require empty orbitals to be able to react with the focal point. Some substrates, such as molecular oxygen, have a basal state of a triplet type, which causes metallic coordinate nuclei with semi-filled orbitals to present a strong tendency to react with such substrates. It is possible to say that molecular oxygen also presents solitary pairs, so it is able to react as a normal Lewis base.
If the ligands surrounding the coordination nucleus are carefully chosen, this central group can be used to catalyze the transformation of other molecules or it can be used as an indicator or sensor.
Contenido relacionado
Hydrazine
Nitric acid
Pharmacology




















![El complejo [UO2(Acetato O, O')3] presenta una geometría bipiramidal hexagonal.](https://upload.wikimedia.org/wikipedia/commons/thumb/e/e1/BipirHexg-%28%28UO2%28acetato-O%2CO%27%293%29%29.png/120px-BipirHexg-%28%28UO2%28acetato-O%2CO%27%293%29%29.png)
![El complejo [Y(OH)8]3+ presenta una geometría tetraédrica triapicada.](https://upload.wikimedia.org/wikipedia/commons/thumb/a/ac/2Deca%C2%B7angular%28%28Y%28OH%298%29%293%2B.png/120px-2Deca%C2%B7angular%28%28Y%28OH%298%29%293%2B.png)
![El complejo [U(CNS)8]4- presenta una clara geometría cúbica.](https://upload.wikimedia.org/wikipedia/commons/thumb/1/12/Cubica%28%28U%28NCS%298%29%294-.png/120px-Cubica%28%28U%28NCS%298%29%294-.png)

![cis-[CoCl2(NH3)4]+](https://upload.wikimedia.org/wikipedia/commons/thumb/b/be/Cis-dichlorotetraamminecobalt%28III%29.png/120px-Cis-dichlorotetraamminecobalt%28III%29.png)
![trans-[CoCl2(NH3)4]+](https://upload.wikimedia.org/wikipedia/commons/thumb/5/56/Trans-dichlorotetraamminecobalt%28III%29.png/120px-Trans-dichlorotetraamminecobalt%28III%29.png)
![fac-[CoCl3(NH3)3]](https://upload.wikimedia.org/wikipedia/commons/thumb/6/69/Fac-trichlorotriamminecobalt%28III%29.png/109px-Fac-trichlorotriamminecobalt%28III%29.png)
![mer-[CoCl3(NH3)3]](https://upload.wikimedia.org/wikipedia/commons/thumb/5/54/Mer-trichlorotriamminecobalt%28III%29.png/120px-Mer-trichlorotriamminecobalt%28III%29.png)
![Λ-[Fe(ox)3]3−](https://upload.wikimedia.org/wikipedia/commons/thumb/d/df/Delta-tris%28oxalato%29ferrate%28III%29-3D-balls.png/110px-Delta-tris%28oxalato%29ferrate%28III%29-3D-balls.png)
![Δ-[Fe(ox)3]3−](https://upload.wikimedia.org/wikipedia/commons/thumb/6/6e/Lambda-tris%28oxalato%29ferrate%28III%29-3D-balls.png/111px-Lambda-tris%28oxalato%29ferrate%28III%29-3D-balls.png)
![Λ-cis-[CoCl2(en)2]+](https://upload.wikimedia.org/wikipedia/commons/thumb/1/12/Delta-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png/78px-Delta-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png)
![Δ-cis-[CoCl2(en)2]+](https://upload.wikimedia.org/wikipedia/commons/thumb/8/81/Lambda-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png/78px-Lambda-cis-dichlorobis%28ethylenediamine%29cobalt%28III%29.png)







