Circumference

format_list_bulleted Contenido keyboard_arrow_down

ImprimirCitar

Circumference with center at point M and radio r

A circle is a flat, closed curve such that all its points are at the same distance from the center.

One circumference is the geometrical place of the points of a plane that equate to another point called center.

Different from circle, whose locus is determined by a circumference, and the region of the plane that encloses it.

History

The interest in knowing the length of a circle arose in Babylon. When they used carts with wheels, it was essential to relate the diameter or radius to the circumference, helping to improve precision when manufacturing the wheels and in turn facilitating transportation.

Frequent terminology

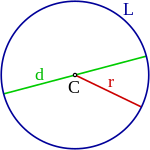
Relevant elements of the circumference, inherited by the circle:

The downtown is the equidistant point to all points of a circumference. Signed with the name $C$ in the figure.
A radio is any segment that unites the center of the circumference with any point of the same. The radio is also the length of the segments of the same name. Signed with the name $r$ in the figure.
A diameter is any segment that unites two points of the circumference passing through its center. The diameter is also the length of the segment of the same name. Signed with the name $d$ in the figure.
The perimeter is the contour of the circumference and its length. Signed with the name $L$ in the figure.
One string is any segment that binds two points of a circumference. The diameter is a maximum length string. Green segment in the figure.
A bow is any portion of circumference bound by two points on this one. It is also said that a string subsidizes every arch that determines its ends. Blue curve line in the figure.
One arrow or sagita regarding a rope is the segment of its mediatrix between this rope and the arch that determines this, without passing through the center. Red segment in the figure.
One semicircunference is any arch bound by the ends of a diameter.

Perimeter

The length of a circle depending on the radio $r$ or diameter ${displaystyle d=2cdot r}$ is:

{displaystyle ell =2pi cdot r=}

{displaystyle pi cdot d}

where ${displaystyle pi =3,14159dots }$ It's the constant pi.

Area

Main article: Circle

The area of the circle or of the region of the plane delimited by a circumference:

A =

{displaystyle {frac {ell cdot r}{2}}=}

{displaystyle pi cdot r^{2}=}

{displaystyle {frac {pi cdot d^{2}}{4}}}

Properties

Only the straights that contain the center of the circumference can be an axis of symmetry of this.
The points of the circumference over any perpendicular to the straight passing through the center are equal to this one. By building an isosceles triangle with two radios and the perpendicular is proven to be equidistant to the straight line that can now be called straight symmetry.

Circumferences are invariant to any rotation with the axis in the center of this circumference.
Trivial after understanding that the radios suffer a rotation, therefore they do not modify their length or their common origin, since it is a displacement of the plane and therefore an isometry.

Relative positions with respect to the circumference

See also: Relative positions in the circle

The Points

Positions of the points with respect to the circumference:

A outer point is the one that is at a distance greater than the radius of the circumference regarding the position of its center.
A inner point is the one that is at a distance less than the radius of the circumference regarding the position of its center.

The lines

Positions of the lines with respect to the circumference:

One Straight outside is any straight that has no points in common with the circumference.
One Straight. is any straight that touches the circumference at a single point.
One straight secante is any straight that cuts the circumference in two points.

The point of tangency is called each of the points that share the circumference with the different tangent elements, that is, the point where the tangency occurs. Tangencies can be made at any point on the circumference.

Properties

All tangent straight to a circumference is perpendicular to the radius that contains the tangence point.
By reduction to the absurd, you can assume that it is not perpendicular, therefore you can build an isosceles triangle with another radius, thus proving that there is another point of tangence different from the first and as this should be unique implies the denial that they are not perpendicular and therefore it is a straight angle.

Between circles

Positions between circles:

A circumference is exterior to another, if all their points are outside this other. See figure 1 and 8.
A circumference is interior to another, if all their points are internal to this other. See figure 5.
One circumference is surrounding another, if all its points are not interior to this other that in turn is not external to the first. See Figures 7 and 8.
A circumference is outside to another, if they have a single common point and all other points of one are external to the other. See figure 2.
A surrounding circumference is tangent outside to another, if they have a single common point. See figure 7.
A circumference is tangent interior to another, if they have a single common point and all other points of one are interior to the other. See figure 4.
A circumference is secante to another, if cut in two different points. See figure 3.
One circumference is orthogonally dry to another, if the angle of its intersection is straight, that is, its tangent straights in each of the intersections are perpendicular.
They are. eccentric the circumferences that do not have the same center.
They are. concentric the circumferences that have the same center, that is, those that are not eccentric.
They are. matching the circumferences that have the same center and the same radius, that is, all the points of one are those of the other and vice versa. See figure 6.

Properties

The centers of the tangent circles are aligned with the point of tangence.
As the tangent line at the point is perpendicular to the radio, it implies that all radios are perpendicular to that tangent line at the same point, that is, all centers are aligned.

Angles in a circle

Position of the angles with respect to a circle, can be:

A central angle is the one who has his vertex in the center of the circumference. See figure 1.
A registered angle is the one who has his vertex on the circumference whose sides determine a string each in the circumference. See figure 2.
A semi-inscribed angle is the one that has its vertex on the circumference and one of its dry sides determines a rope and the other a tangent straight to the circumference, that is, the vertex is a point of tangence. See figure 3.
A Ex-registered angle is the one that has its vertex on the circumference and one of its sides determines a string and the extension of the other determines another string, that is, the outer angle of a registered angle. See figure 4.
A interior is the one who has his vertex inside the circumference. See figure 5.
A outer angle is the one that has its vertex on the outside of the circumference and each side is tangent or secant to the circumference. See Figures 6.7 and 8.

Properties

At the central angle its width $alpha$ and radio $r$ of the circumference, determines the length of the arch ${displaystyle ell}$ highlighted in the figure in blue. If the angle is in degrees:

${displaystyle ell _{alpha }=}$ ${displaystyle {frac {alpha }{180^{circ }}}cdot pi cdot r}$
The central angle indicates what circumference fraction the bow has, so if ${displaystyle ell =2pi cdot r=}$ Then: ${displaystyle ell _{alpha }={frac {alpha }{360^{circ }}}cdot 2pi cdot r}$ That is, the arch is directly proportional to the central angle, and that simplifying the desired formula remains.

If the angle is in radians:

{displaystyle ell _{alpha }=}

{displaystyle alpha cdot r}

Main article: Arc capable

The capable arc relates the central, inscribed, semi-inscribed and ex-inscribed angle as long as the intersections of the sides maintain the same distance.

If the registered, semi-inscribed and ex-inscribed angle has the same width $alpha$ , then, determine the same arc length, blue in the image, on the same radius circumference $r$ . If the angle is in degrees:

${displaystyle ell _{alpha }=}$ ${displaystyle {frac {alpha }{90^{circ }}}cdot pi cdot r}$
As the central angle measures the double that the inscribed, semi-inscribed and ex-inscribed angle, this fact is replaced in the formula used in the central angle being: ${displaystyle ell _{alpha }={frac {2cdot alpha }{360^{circ }}}cdot 2pi cdot r}$ Simplifying the desired formula.

If the angle is in radians:

{displaystyle ell _{alpha }=}

{displaystyle alpha cdot 2cdot r}

Diverse types of angles appear in the analysis of the power of a point with respect to a circumference.

Enrollment and constituency

We will say that a circle is circumscribed to a polygon when all the vertices of said polygon are on it, it is said that this polygon is inscribed.

We will say that a circle is inscribed to a polygon when it is tangent to all the sides of said polygon, it is said that this polygon is circumscribed.

Circumference representation

Circumference can be represented by equations or functions that determine the position of each of its points. To do this it is only necessary to ensure that the distance of each point $P$ of the circumference to its center $C$ be constant for each of the equations and functions you have.

Equation of the circle

radio circle two in a coordinate system

A circumference is determined by a centre ${displaystyle C=(a,,b)}$ and a radio $r$ therefore his equation is determined by imposing that the distance from his points, ${displaystyle P=(x,,y)}$ The center is constant, that is, ${displaystyle |P-C|=r}$ giving the following equation:

{displaystyle (x-a)^{2}+(y-b)^{2}=r^{2}.}

Your representation in a coordinate system is given by each point of form ${displaystyle (x,,y)}$ that satisfy the equation.

The previous equation is easier if it is centered on the origin of coordinates ${displaystyle C=(0,,0):}$

{displaystyle x^{2}+y^{2}=r^{2}.}

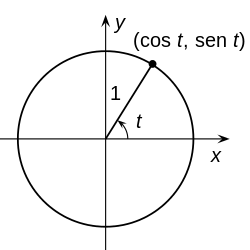
The circle with the center at the origin of coordinates and radius one is called the unit circle or goniometric circle and its equation is:

{displaystyle x^{2}+y^{2}=1.}

Your implicit function is ${displaystyle f(x,,y)=x^{2}+y^{2}-1}$ and to represent the circumference are sought the points of the plane that fulfill the equation ${displaystyle f(x,,y)=0.}$

Properties

It is possible to use squares to find the circumference equation from its extended equation:

${displaystyle x^{2}+y^{2}+Dx+Ey+F=0}$
Applying square to square ${displaystyle x^{2}+Dx}$ and ${displaystyle y^{2}+Ey}$ it follows that: ${displaystyle a=-{frac {D}{2}}}$ ${displaystyle b=-{frac {E}{2}}}$ and therefore ${displaystyle (x-a)^{2}+(y-b)^{2}=a^{2}+b^{2}-F}$ from where: ${displaystyle r={sqrt {a^{2}+b^{2}-F}}.}$

From the extreme points of a diameter, ${displaystyle (x_{1},y_{1})}$ and ${displaystyle (x_{2},y_{2})}$ the equation of the circumference is:

${displaystyle (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=0.}$
It is only necessary to extend the product of the given equation to identify the circumference: ${displaystyle (x-x_{1})(x-x_{2})+(y-y_{1})(y-y_{2})=}$ ${displaystyle x^{2}-xcdot x_{1}-xcdot x_{2}+x_{1}cdot x_{2}+y^{2}-ycdot y_{1}-ycdot y_{2}+y_{1}cdot y_{2}}$ Finally it should be noted that the two points cancel the equation and prove that the middle point is the center.

Parametric function

Circle with center in ${displaystyle C=(a,,b)}$ and radio $r$ can be parameterized using single parameter trigonometric functions $theta$ for a parametric function ${displaystyle r_{C}(theta)=(x,,y):}$

{displaystyle {begin{array}{l}x=a+r,cos theta \y=b+r,operatorname {sen} theta end{array}}}

{displaystyle theta in [0,,2,pi)}

You can also parameterize rational functions like

${displaystyle {begin{array}{l}x=a+rleft({frac {1-t^{2}}{1+t^{2}}}right)\y=b+rleft({frac {2t}{1+t^{2}}}right)end{array}}}$ ${displaystyle tin {bar {mathbb {R} }}}$
First a straight beam of the type is used ${displaystyle y=ax}$ to project values $t$ on the vertical straight ${displaystyle x=1}$ that will be the way ${displaystyle (1,,t)}$ and projecting will be shaped ${displaystyle (a,,acdot t)}$ . Projection on horizontal straight. If replaced on the unit circumference ${displaystyle (x-1)^{2}+y^{2}=1,}$ will give us the interference of the projection on this circumference and therefore the points of this parametrically: ${displaystyle (a-1)^{2}+(acdot t)^{2}=1Leftrightarrow }$ ${displaystyle a^{2}cdot (1+t^{2})=2cdot aRightarrow }$ ${displaystyle a={frac {2}{1+t^{2}}}}$ finally replacing over the beam and fixing the fractions remains ${displaystyle left({frac {1-t^{2}}{1+t^{2}}},,{frac {2cdot t}{1+t^{2}}}right)}$

where ${displaystyle {bar {mathbb {R} }}}$ includes the point in the infinite.

Parametric function in the complex plane

In the complex plane, a circle with center ${displaystyle C=a+i,b}$ and radio $r$ from the circumference equation ${displaystyle |z-c|=r}$ the parametric form is obtained:

{displaystyle z=re^{itheta }+C=}

{displaystyle r(cos theta +ioperatorname {sen} theta)+a+i,b}

where ${displaystyle theta in [0,,2,pi).}$

Vector function

As in parametric function, circumference can be represented in any two-dimensional subspace of a vector space using two orthonormal vectors $vec{u}$ and $vec{v}$ , and therefore generators of that subspace, allowing to build the circumference in any oblique plane with center ${displaystyle {vec {c}}}$ and radio $r$ which is given or described by the vector function:

{displaystyle r(theta)=}

{displaystyle {vec {c}}+{vec {u}}rcos theta +{vec {v}}roperatorname {sen} theta }

where

{displaystyle theta in [0,,2pi).}

Equation in Polar Coordinates

Unit circle.

All flat curve given in polar coordinates is shape ${displaystyle alpha (theta)=}$ ${displaystyle (rho (theta)cos theta,rho (theta)operatorname {sen} theta)}$ where ${displaystyle rho (theta)}$ is the distance to the center or pole $O$ and $theta$ the angle regarding the OX axis, therefore the expression of a circle with center at the pole and radius $r$ is:

${displaystyle alpha (theta)=}$ ${displaystyle (rcos theta,roperatorname {sen} theta)}$
The curve ${displaystyle alpha (theta)}$ must fulfill the equation: ${displaystyle x^{2}+y^{2}=r^{2}.}$ I mean: ${displaystyle (rho (theta)cos theta)^{2}+(rho (theta)operatorname {sen} theta)^{2}=r^{2}.}$ From where it deduces that ${displaystyle rho (theta)=r}$

When the center is at the point ${displaystyle (d,0)}$ with radio $r$ the circumference is:

${displaystyle alpha (theta)=}$ ${displaystyle (rho (theta)cos theta,rho (theta)operatorname {sen} theta)}$ where ${displaystyle rho (theta)=}$ ${displaystyle dcos theta +{sqrt {r^{2}-d^{2}operatorname {sen} theta }}}$
Extending the circumference equation: ${displaystyle (x-d)^{2}+y^{2}=r^{2}Rightarrow }$ ${displaystyle x^{2}-2xcdot d+d^{2}+y^{2}=r^{2}Rightarrow }$ ${displaystyle x^{2}+y^{2}-2xcdot d+d^{2}-r^{2}=0.}$ Change is made ${displaystyle x=rho (theta)cos theta }$ and ${displaystyle y=rho (theta)operatorname {sen} theta }$ and is simplified as: ${displaystyle rho (theta)^{2}-2rho (theta)dcos theta +d^{2}-r^{2}=0Rightarrow }$ ${displaystyle rho (theta)=}$ ${displaystyle dcos theta pm {sqrt {r^{2}-d^{2}operatorname {sen} theta }}.}$ Finally it takes the positive root to $0.}" xmlns="http://www.w3.org/1998/Math/MathML">ρ ρ (θ θ )▪0.{displaystyle rho (theta) 20050. !0.}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/744eb70deb531c085364012edd120250ee280425" style="vertical-align: -0.838ex; width:9.009ex; height:2.843ex;"/>$ The pole cannot be external to the circumference because the parameter domain is not continually defined in parameterization.

Property

Given three unaligned points ${displaystyle (x_{1},,y_{1}),,(x_{2},,y_{2})}$ and ${displaystyle (x_{3},,y_{3})}$ There is a single circumference that contains these three points, that is, this circumference will be circumscribed to the triangle defined by these points. The circumference equation is given by the matrix determinant:

{displaystyle det {begin{bmatrix}x&y&x^{2}+y^{2}&1\x_{1}&y_{1}&x_{1}^{2}+y_{1}^{2}&1\x_{2}&y_{2}&x_{2}^{2}+y_{2}^{2}&1\x_{3}&y_{3}&x_{3}^{2}+y_{3}^{2}&1\end{bmatrix}}=0.}

Ways to identify circles

Depending on your area of expertise, there are ways to implicitly identify and use a circle, as well as its functions and equations.

In topology

In topology, it is called circumference to any single closed curve that is homeomorph to the usual circumference of geometry (i.e., the 1–dimensional sphere). It can be defined as the quotient space determined by identifying as one the two ends of a closed interval. However, the geometres call the circumference 2-sphere, while the topologists refer to it as 1-sphere and indicate it as ${displaystyle S^{1},!}$ , giving rise to possible confusions.

The dimension of the circle is 1. Similarly, the dimension of an unbounded line, or of an arc — that is, of a homeomorphic set with a closed interval — and of a simple closed curve, i.e. a homeomorphic set with a circumference, is equal to 1. Also the case of a closed polygonal.

In Differential Equations

In the topic of differential equations, a circumference can be determined by an integral curve of a differential equation as:

{displaystyle {begin{array}{l}x'=-y\y'=,xend{array}}}

In differential geometry of curves

In local theory of the curve, a curve of constant curvature without torsion is considered as a circumference.

Particular circumferences

Cardanus circles

A pair of circumferences that move, tangentially and internally, one over the other keeping a ratio between their radii of 1:2. Originally investigated by the Italian mathematician Girolamo de Cardano

Directive circle

Used in an alternative definition of the ellipse and the hyperbola. These being the place of the centers of the tangent circles to the so-called directrix circle.

Osculating circumference

When dealing with the curvature of a curve or a surface, at the point of contact, in addition to the tangent, the circumference of the curvature is taken into account, called the osculating circumference

Contenido relacionado

Más resultados...