Chemical balance

ImprimirCitar

In a chemical process, chemical equilibrium is the state in which the chemical activities or concentrations of reactants and products have no net change. Normally, this would be the state that occurs when a reversible reaction evolves forward at the same rate as its reverse reaction. The reaction rates of the forward and reverse reactions are usually not zero, but if both are the same, there is no net change in either the concentrations of the reactants or products. This process is called dynamic equilibrium.

A bureta; an apparatus to perform an acid-base valuation, is an important part of balance chemistry.

Introduction

In a chemical reaction, when reactants are mixed in a reaction vessel of aqueous solution (with heating, if necessary), not all of the reactants are converted to products. After some time (which depends on the compounds that make up the mixture), the opposite reactions can reach equal reaction rates, creating a dynamic equilibrium in which the ratio between reactants and products will be fixed.

The concept of chemical equilibrium was developed after Berthollet (1803) found that some chemical reactions are reversible. For a reaction, such as

{displaystyle alpha mathrm {A} +beta mathrm {B} rightleftharpoons sigma mathrm {S} +tau mathrm {T} }

can be in balance, direct and reverse reaction speeds have to be equal. In this chemical equation, with arrows pointing in both directions to indicate balance, ${displaystyle mathrm {A} }$ and ${displaystyle mathrm {B} }$ are the chemical species that react ${displaystyle mathrm {S} }$ and ${displaystyle mathrm {T} }$ are the product species, and $alpha$ , $beta$ , $sigma$ and $tau$ are the schiometric coefficients of reactants and products. The balance position of the reaction is said to be very shifted to the right, if, in the balance, almost all the reagents have been used and to the left if only some product is formed from the reagents.

Guldberg and Waage (1864), based on Berthollet's ideas, proposed the law of mass action:

Forward Reaction Rate:

${displaystyle v=k_{+}{A}^{alpha }{B}^{beta },!}$

Reverse reaction rate:

${displaystyle v=k_{-}{S}^{sigma }{T}^{tau },!}$

where $A$ , $B$ , $S$ and $T$ are active masses and ${displaystyle k_{+}}$ and ${displaystyle k_{-}}$ It's the speed constants. When the speeds of direct and reverse reaction are equal:

${displaystyle k_{+}left{Aright}^{alpha }left{Bright}^{beta }=k_{-}left{Sright}^{sigma }left{Tright}^{tau },}$

and the relationship between the rate constants is also a constant, now known as the equilibrium constant.

${displaystyle K={frac {k_{+}}{k_{-}}}={frac {{S}^{sigma }{T}^{tau }}{{A}^{alpha }{B}^{beta }}}}$

By convention, products are the numerator. However, the law of mass action is valid only for one-step reactions that proceed through a single transition state and is not valid, in general, because the rate equations generally follow stoichiometry. of the reaction as Guldberg and Waage proposed (see, for example, the aliphatic nucleophilic substitution by SN1 or the reaction of hydrogen and bromine to form hydrogen bromide). The equality of the rates of the forward and reverse reactions is a necessary condition for chemical equilibrium, although it is not sufficient to explain why equilibrium occurs. Despite the failure of this derivation, the equilibrium constant for a reaction is in fact a constant, independent of the activities of the various species involved, although it does depend on temperature, as seen by the van't Hoff equation.. The addition of a catalyst affects both the forward and reverse reactions in the same way and will not have an effect on the equilibrium constant. The catalyst speeds up the rate of both reactions thereby increasing the rate at which equilibrium is reached.

Although macroscopic equilibrium concentrations are constant over time, reactions occur at the molecular level. For example, in the case of acetic acid being dissolved in water and the formation of acetate and hydronium ions,

{displaystyle {rm {CH_{3}CO_{2}H+H_{2}Orightleftharpoons CH_{3}CO_{2}^{-}+H_{3}O^{+}}}}

A proton can jump from an acetic acid molecule to a water molecule and then to an acetate ion to form another acetic acid molecule, leaving the number of acetic acid molecules unchanged. This is an example of dynamic equilibrium. Equilibria, like the rest of thermodynamics, are statistical phenomena, the averages of microscopic behavior.

Le Châtelier's principle (1884) is a useful principle that gives a qualitative idea of the response of an equilibrium system to changes in reaction conditions. If a dynamic equilibrium is disturbed by changing conditions, the equilibrium position is shifted to counteract the change. For example, adding more S from the outside will produce an excess of products, and the system will try to counteract this change by increasing the reverse reaction and pushing the equilibrium point back (although the equilibrium constant will remain the same).

If a mineral acid is added to the acetic acid mixture, as the concentration of the hydronium ion increases, dissociation should decrease as the reaction shifts to the left, consistent with this principle. This can also be deduced from the expression for the equilibrium constant for the reaction:

${displaystyle K={rm {frac {{CH_{3}CO_{2}^{-}}{H_{3}O^{+}}}{{CH_{3}CO_{2}H}}}}}$

if {H₃O⁺} increases {CH₃CO₂H} must increase and { CH₃CO₂⁻} should decrease.

H₂O is left out since it is a pure liquid and its concentration is not defined.

A quantitative version is given by the reaction quotient.

J.W. Gibbs suggested in 1873 that equilibrium is reached when the Gibbs energy of the system is at its minimum (assuming that the reaction is carried out at constant pressure). What this means is that the derivative of the Gibbs energy with respect to the reaction coordinate (a measure of the extent to which the reaction has occurred, ranging from zero for all reactants to a maximum for all products) vanishes, pointing to a stationary point. This derivative is often called, for certain technical reasons, the Gibbs energy shift. This criterion is both necessary and sufficient. If a mixture is not in equilibrium, the release of excess Gibbs energy (or Helmholtz energy in constant volume reactions) is the "driver" which changes the composition of the mixture until equilibrium is reached. The equilibrium constant can be related to the standard Gibbs free energy change of the energy for the reaction by means of the equation:

${displaystyle Delta _{mathrm {r} }G^{ominus }=-RTln K_{mathrm {eq} }}$

where $R$ is the universal constant of gases and $T$ temperature.

When the reactants are dissolved in a medium of high ionic force the quotient of the activity coefficients can be taken as a constant. In this case, the quotient of concentrations is, ${displaystyle K_{c}}$ ,

${displaystyle K_{c}={frac {[S]^{sigma }[T]^{tau }}{[A]^{alpha }[B]^{beta }}}}$

where ${displaystyle [A]}$ is the concentration of $A$ , etc, is independent of the analytical concentration of the reagents. For this reason, equilibrium constants for solutions are often determined by high ionic force means. ${displaystyle K_{c}}$ varies with ionic strength, temperature and pressure (or volume). Likewise ${displaystyle K_{P}}$ for gases depends on partial pressure. These constants are easier to measure and are in higher chemistry courses.

Thermodynamics

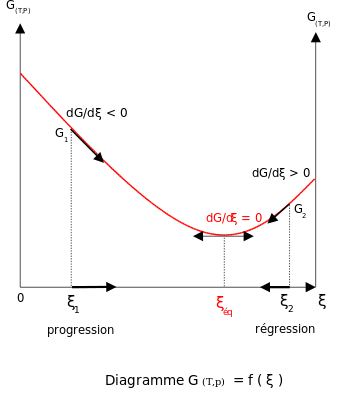
The relationship between Gibbs' energy and the balance constant can be found considering chemical potentials. At constant temperature and pressure, Gibbs' free energy $G$ of reaction only depends on the extent of the reaction ( $xi$ ), and can only decrease according to the second law of thermodynamics. This means the derivative of $G$ depending on $xi$ must be negative if the reaction occurs. In balance, the derivative is equal to zero.

${displaystyle left({frac {partial G}{partial xi }}right)_{T,p}=0~}$ .

If the reaction were to take place at constant volume, the Helmholtz energy should be considered.

Only the case of constant pressure is considered in this article. The constant volume case is important in geochemistry and atmospheric chemistry, where pressure variations are important. It should be noted that if the reactants and products are in their standard state (completely pure), then there would be no reversibility or equilibrium. The mixing of products and reactants contributes a large amount of entropy (known as the entropy of mixing) to states that contain equal parts mixtures of products and reactants. The combination of the standard Gibbs energy change and the mixing Gibbs energy determines the equilibrium state.

In general, a system in equilibrium is defined by writing an equilibrium equation for the reaction

<math alttext="{displaystyle alpha ,{ce {A}}+beta ,{ce {B }},sigma ,{ce {S}}+tau ,{ce {T}}}" xmlns="http://www.w3.org/1998/Math/MathML">α α A+β β B − − − − σ σ S+Δ Δ T{displaystyle alpha ,{ce {A}}+beta ,{ce {B θ}},sigma ,{ce {S}+tau ,{ce {T}}}}}}}<img alt="{displaystyle alpha ,{ce {A}}+beta ,{ce {B }},sigma ,{ce {S}}+tau ,{ce {T}}}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/3b2317f7c2c1eb2fee5daf59a6aa731259ad40b0" style="vertical-align: -0.671ex; width:23.33ex; height:3.009ex;"/>

This system will take place if and only if the condition of chemical equilibrium is met, that is

${displaystyle sum _{i}nu _{i}mu _{i}=0}$ ,

where ${displaystyle mu _{i}}$ is the chemical potential of i- that chemical species and ${displaystyle nu _{i}}$ their respective schiometric coefficient, such that $<math alttext="{displaystyle nu _{i}.. i.0{displaystyle nu _{i} implied}<img alt="{displaystyle nu _{i}$ for reagents and $0}" xmlns="http://www.w3.org/1998/Math/MathML">.. i▪0{displaystyle nu _{i} 20050}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/44d9c0eac121342f83f680ea9963901ddfded18f" style="vertical-align: -0.671ex; width:6.209ex; height:2.509ex;"/>$ for the products.

The chemical potential is equal to the partial molar Gibbs energy, since

${displaystyle mu _{i}=left({frac {partial G}{partial n_{i}}}right)_{T,p,n_{jneq i}}}$ ,

where $n_{i}$ is the amount of substance i (in moles).

In order to satisfy the condition of chemical equilibrium, the Gibbs energy must be stationary, which means that the partial derivative of G with respect to the reaction coordinate ξ must be null.

${displaystyle left({frac {partial G}{partial xi }}right)_{T,p}=0~}$ .

From the definition of the Gibbs energy, a new expression of the chemical potential as a function of activity can be obtained, such that

${displaystyle mu _{i}=mu _{i}^{circ }+RTln a_{i},}$ ,

where ${displaystyle mu _{i}^{circ }}$ is the standard chemical potential of i- That's a species.

Substitute expressions like this into the Gibbs energy equation:

${displaystyle mathrm {d} G=V,mathrm {d} p-S,mathrm {d} T+sum _{i}mu _{i},mathrm {d} N_{i}}$ ,

in the case of a closed system.

${displaystyle mathrm {d} N_{i}=nu _{i},mathrm {d} xi ,}$ .

At constant pressure and temperature we obtain:

${displaystyle left({frac {partial G}{partial xi }}right)_{T,p}=sum _{i}nu _{i}mu _{i}=Delta _{rm {r}}G_{T,p}}$

which corresponds to the change in the Gibbs energy for the reaction.

Exampling for the mentioned reaction,

${displaystyle Delta _{rm {r}}G_{T,p}=sigma mu _{rm {S}}+tau mu _{rm {T}}-alpha mu _{rm {A}}-beta mu _{rm {B}},}$

Substituting chemical potentials:

${displaystyle Delta _{rm {r}}G_{T,p}=(sigma mu _{rm {S}}^{circ }+tau mu _{rm {T}}^{circ })-(alpha mu _{rm {A}}^{circ }+beta mu _{rm {B}}^{circ })+(sigma RTln a_{rm {S}}+tau RTln a_{rm {T}})-(alpha RTln a_{rm {A}}+beta RTln a_{rm {B}})}$

The relationship becomes

${displaystyle Delta _{rm {r}}G_{T,p}=sum _{i}nu _{i}mu _{i}^{circ }+RTln {frac {a_{rm {S}}^{sigma }a_{rm {T}}^{tau }}{a_{rm {A}}^{alpha }a_{rm {B}}^{beta }}}}$ ,

where:

${displaystyle sum _{i}nu _{i}mu _{i}^{circ }=Delta _{rm {r}}G^{circ }}$ ,

which is the standard Gibbs energy change of the reaction.

The relationship can be expressed generically such that

${displaystyle Delta _{rm {r}}G_{T,p}=sum _{i}nu _{i}mu _{i}^{circ }+RTln prod _{i}a_{i}^{nu _{i}}}$ .

It is also possible to determine a constant at a given temperature that can be calculated using thermodynamic tables,

${displaystyle Q=prod _{i}a_{i}^{nu _{i}}}$ ,

being $Q$ the reaction quotient when the system is not in balance.

Therefore:

${displaystyle left({frac {partial G}{partial xi }}right)_{T,p}=Delta _{rm {r}}G_{T,p}=Delta _{rm {r}}G^{circ }+RTln Q}$ .

In equilibrium:

${displaystyle left({frac {partial G}{partial xi }}right)_{T,p}=Delta _{rm {r}}G_{T,p}=0}$ ,

so,

${displaystyle Q=K^{circ }~}$ ,

where ${displaystyle K^{circ }}$ It's the constant balance.

This leads to:

${displaystyle Delta _{rm {r}}G^{circ }+RTln K^{circ }=0}$

and

${displaystyle Delta _{rm {r}}G^{circ }=-RTln K^{circ }}$

Obtaining the energy change value of Gibbs standard, allowing the calculation of the balance constant

Changes in equilibrium with the addition of reactants or products

For a reacting system in equilibrium:

${displaystyle {begin{cases}Q=K^{circ }\xi =xi _{rm {eq}}end{cases}}}$

If its value of the equilibrium constant, the addition of substance modifies the activities of the components and therefore equilibrium is lost, such that

${displaystyle Qneq K^{circ }~}$

Therefore:

${displaystyle left({frac {partial G}{partial xi }}right)_{T,p}=Delta _{rm {r}}G^{circ }+RTln Q~}$

and

${displaystyle Delta _{rm {r}}G^{circ }=-RTln K^{circ }~}$

then

${displaystyle left({frac {partial G}{partial xi }}right)_{T,p}=RTln {frac {Q}{K^{circ }}}~}$

Knowing that:

${displaystyle Q=prod _{i}a_{i}^{nu _{i}}~}$

So:

If the activity of a reactive increases, the reaction quotient decreases:

$<math alttext="{displaystyle QQ.K {displaystyle Q prescriptionK^{circ}~}<img alt="{displaystyle Q$

and

$<math alttext="{displaystyle left({frac {partial G}{partial xi }}right)_{T,p}(▪ ▪ G▪ ▪ roga roga )T,p.0{displaystyle left({frac {partial G}{partial xi}}{right)_{T,p}{partial G}{partial xi}}}}{right)<img alt="{displaystyle left({frac {partial G}{partial xi }}right)_{T,p}$

The reaction will move to the right (i.e., in the direction of the forward reaction), and therefore more products will be formed.

If the activity of a product increases, then:

$K^{circ }~}" xmlns="http://www.w3.org/1998/Math/MathML">Q▪K {displaystyle Q 2005K^{circ}~}K^{circ }~}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/6cf48cb2b6aa68aac2cafb949bc5c49db0863872" style="vertical-align: -0.671ex; width:8.666ex; height:2.676ex;"/>$

and

$0~}" xmlns="http://www.w3.org/1998/Math/MathML">(▪ ▪ G▪ ▪ roga roga )T,p▪0{displaystyle left({frac {partial G}{partial xi}}}{right)_{T,p} 20050~}0~}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/fcff50ef1d8b5bb693333023cb3b8062addf9a9d" style="vertical-align: -2.838ex; width:14.917ex; height:6.509ex;"/>$

The reaction will shift to the left (that is, in the direction of the reverse reaction, and therefore fewer products will be formed. Note that the activities and the equilibrium constants are numbers, dimensionless.

Activity treatment

When a solution is available, the activity of the solute can be expressed such that

${displaystyle a_{i}={frac {c_{i}}{c^{circ }}}gamma _{i}}$ .

Consequently, the expression of the balance constant can be written as the product of the balance constant in concentrations ${displaystyle K_{c}}$ and the product of the activity coefficients,

${displaystyle K=prod _{i}c_{i}^{nu _{i}}prod _{i}gamma _{i}^{nu _{i}}}$ ,

where $c_i$ is the concentration of the i- That's a chemical species. It is possible, in principle, to obtain the values of the activity coefficients ${displaystyle gamma _{i}}$ . For this, when electrolytes are available, equations such as Debye-Hückel or extensions such as the Davies equation, or the Pitzer equations, can be used, ^{Software (low)}. However, this is not always possible. It is a common practice in areas such as analytical chemistry to assume that the product of activity coefficients is a constant, and to use the constant balance in concentrations at the place of constant balance.

For gaseous phase reactions the balance coefficient is used in pressures rather than in concentrations. The use of the leakage coefficient is common $phi$ instead of the coefficient of activity. In industry, for example, during ammonia synthesis, the leakage coefficients should be taken into account. The fleeting $f$ , which is a magnitude with pressure units, is defined as

${displaystyle f_{i}=lambda _{i}lim _{pto 0}left({frac {p_{i}}{lambda _{i}}}right)_{T}}$ ,

where ${displaystyle lambda _{i}}$ is the absolute activity of i- That's a species. ${displaystyle lambda _{i}=exp(mu _{i}/RT)}$ . An equivalent expression of escape is

${displaystyle f_{i}=phi _{i}p_{i}}$ ,

where ${displaystyle p_{i}}$ is partial pressure and ${displaystyle phi _{i}}$ their respective fleeting coefficient.

If the activity of a species in the gas phase can be expressed as

${displaystyle a_{i}^{rm {g}}={frac {p_{i}}{p^{circ }}}gamma _{i}^{rm {g}}}$ ,

its chemical potential will be given by

${displaystyle mu _{i}^{rm {g}}=mu ^{circ }+RTln a_{i}=mu ^{circ }+RTln {frac {f_{i}}{f^{circ }}}=mu ^{circ }+RTln phi _{i}p_{i}}$ ,

so the general expression that defines the equilibrium constant is valid for both solution and gas phases.

Rationale for the use of the equilibrium constant in concentrations

In aqueous solution, equilibrium constants are generally determined in the presence of an “inert” electrolyte such as sodium nitrate (NaNO₃) or potassium perchlorate (KClO₄). The ionic strength, I, of a solution containing electrolytes is given by:

${displaystyle I_{c}={frac {1}{2}}sum _{i}c_{i}z_{i}^{2}}$

where ${displaystyle z_{i}}$ represents the load number. When the concentration of dissolved salt is much greater than the concentrations of reagent analysis, the ionic force is indeed constant. Since the activity coefficients depend on the ionic force, the activity coefficients of the species are independent of the concentration. Thus, the assumption that the activity coefficient product is constant is justified. The constant balance in concentrations is a simple multiple of the balance constant.

${displaystyle K_{c}=prod _{i}a_{i}^{nu _{i}}prod _{i}gamma _{i}^{-nu _{i}}}$

However, K_c will vary with ionic strength. If measured at a number of different ionic strengths, the ionic strength value can be extrapolated to zero. The equilibrium constant in concentrations obtained in this way is known, paradoxically, as an equilibrium constant. To use a published value of an equilibrium constant under ionic strength conditions different from the conditions applied in its determination, the value must be set to ^{Software (below)}.

Metastable Mixtures

A mixture may appear to have no tendency to change, even though it is not in equilibrium. For example, a mixture of SO₂ and O₂ is metastable since there is a kinetic barrier to the formation of the product, SO3.

2SO₂ + O₂

{displaystyle rightleftarrows }

2SO₃

The barrier can be overcome when a catalyst is also present in the mixture, such as in the contact method, but the catalyst does not affect the equilibrium concentrations. Similarly, the formation of bicarbonate from carbon dioxide and water is a very slow reaction under normal conditions.

CO₂ + 2H₂O

{displaystyle rightleftarrows }

HCO₃^- +H₃O⁺

but almost instantaneous in the presence of the enzyme carbonic anhydrase.

Pure compounds in equilibrium

When pure substances (liquids or solids) are involved in equilibria, they do not appear in the equilibrium equation. Applying the general formula for an equilibrium constant in the specific case of acetic acid, we obtain

{displaystyle {rm {CH_{3}CO_{2}H+H_{2}Orightleftarrows CH_{3}CO_{2}^{-}+H_{3}O^{+}}}}

${displaystyle K_{c}={rm {frac {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]}{[{CH_{3}CO_{2}H}][{H_{2}O}]}}}}$

The concentration of water can be assumed to be constant. This hypothesis is valid for all solutions except highly concentrated ones. The expression for the equilibrium constant is therefore usually written as

${displaystyle K={rm {frac {[{CH_{3}CO_{2}}^{-}][{H_{3}O}^{+}]}{[{CH_{3}CO_{2}H}]}}}}$

where now ${displaystyle K=K_{c}cdot {rm {[H_{2}O],}}}$ is a constant factor incorporated into the constant balance. A particular case is the self-ionisation of water

{displaystyle {rm {H_{2}O+H_{2}Orightleftarrows H_{3}O^{+}+OH^{-}}}}

The self-ionization constant of water is defined as:

${displaystyle K_{mathrm {w} }={rm {[H^{+}][OH^{-}],}}}$

It is perfectly legitimate to write [H⁺] for the hydrogen ion concentration, since the solvation state of the proton is constant (in dilute solutions) and thus does not affect equilibrium concentrations. K_w varies with variation in ionic strength and/or temperature. The concentrations of H⁺ and OH^- are not independent quantities. Most of the time [OH^-] is replaced by K_w[H⁺]^-1 in the expressions of the equilibrium constant that contain hydroxide. Solids also do not appear in the equilibrium constant equation. An example is the Boudouard reaction:

{displaystyle {rm {2COrightleftarrows CO_{2}+C}}}

for which the equation of the equilibrium constant (without solid carbon) is written as

${displaystyle K_{c}={rm {frac {[CO_{2}]}{[CO]^{2}}}}}$

Multiple balances

Let us consider the case of a dibasic acid H₂. When dissolved in water, the mixture will contain H₂A, HA^-, and A^2-. This equilibrium can be divided into two steps in each of which a proton is released.

{displaystyle mathrm {H_{2}Arightleftarrows HA^{-}+H^{+}}qquad K_{1}=mathrm {frac {[HA^{-}][H^{+}]}{[H_{2}A]}} }

{displaystyle mathrm {HA^{-}rightleftarrows A^{2-}+H^{+}}qquad K_{2}=mathrm {frac {[A^{2-}][H^{+}]}{[HA^{-}]}} }

K₁ and K₂ are examples of “successive” balance constants. The “global” balance constant ${displaystyle beta _{D}}$ , is the product of successive constants

{displaystyle mathrm {H_{2}Arightleftarrows A^{2-}+2H^{+}}qquad beta _{D}=mathrm {frac {[A^{2-}][H^{+}]^{2}}{[H_{2}A]}} {=K_{1}K_{2}}.}

Note that these constants are dissociation constants because the products on the right hand side of the equilibrium expression are the dissociation products. In many systems, it is preferable to use association constants

{displaystyle mathrm {A^{2-}+H^{+}rightleftarrows HA^{-}}qquad beta _{1}=mathrm {frac {[HA^{-}]}{[A^{2-}][H^{+}]}} }

{displaystyle mathrm {A^{2-}+2H^{+}rightleftarrows H_{2}A}qquad beta _{2}=mathrm {frac {[H_{2}A]}{[A^{2-}][H^{+}]^{2}}} }

$beta_1$ and ${displaystyle beta _{2}}$ are examples of constant association. It is evident that ${displaystyle beta _{1}=1/K_{2}}$ and ${displaystyle beta _{2}=1/beta _{D}}$ ; ${displaystyle log beta _{1}=mathrm {p} K_{2}}$ and ${displaystyle log beta _{2}=mathrm {p} K_{2}+mathrm {p} K_{1}}$ . For multiple equilibrium systems, see also: theory of response reactions.

The effect of temperature change on the equilibrium constant

The effect of a temperature change on the equilibrium constant is given by the Van't Hoff equation

{displaystyle {frac {mathrm {d} ln K}{mathrm {d} T}}={frac {{Delta H_{rm {m}}}^{Theta }}{RT^{2}}}}

So, for exothermal reactions ( $<math alttext="{displaystyle Delta HΔ Δ H.0{displaystyle Delta H vis0} <img alt="{displaystyle Delta H$ ), $K$ decreases with increased temperature, but, for endothermal reactions ( $0}" xmlns="http://www.w3.org/1998/Math/MathML">Δ Δ H▪0{displaystyle Delta H/20050}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/21567a214f6fc83612375613d3fd0ea4043be89c" style="vertical-align: -0.338ex; width:8.26ex; height:2.176ex;"/>$ ), $K$ increases with a temperature increase. An alternative formulation is

{displaystyle {frac {mathrm {d} ln K}{mathrm {d} (1/T)}}=-{frac {{Delta H_{rm {m}}}^{Theta }}{R}}}

At first glance this seems to offer a means to obtain the standard grinding of the reaction by studying the variation $K$ with the temperature. In practice, however, the method is unreliable, due to the spread of errors, and almost always very large errors are obtained in the values calculated in this way.

Types of balance and some applications

In the gas phase. Rocket engines
In industrial synthesis, such as ammonia in the Haber-Bosch process that is carried out through a succession of stages of balance, including absorption processes.
Chemistry of the atmosphere
Seawater and other natural waters: Chemical Oceanography
Distribution between two phases
1. LogD Distribution Coefficient: Important for the pharmaceutical industry, where lipophilia is an important property of a drug
2. Liquid-liquid extraction, Ionic exchange, Chromatography
3. product Solubility
4. Captation and release of oxygen by hemoglobin in the blood
Acid/base balance: acid dissociation constant, hydrolysis, tampon solutions, Indicators, Acid-base Homeostasis

Metal-lighting Complexion: Burning Agents, Chelation Therapy, Contrast Reactives for RM, Schlenk Balance
Aduct formation: chemical Host-guest, supramolecular chemistry, molecular recognition, dinitrogen tetroxide
In some oscillating reactions, the approach to balance is not asymptotic, but in the form of a damp oscillation.
Nernst's well-known electrochemical equation gives the difference of electrode potential as a function of redox concentrations.
When molecules on each side of the balance are able to react irreversibly in secondary reactions, the proportion of the final product is determined according to the principle of Curtin-Hammett.

In these applications, terms such as stability constant, formation constant, binding constant, affinity constant, association/dissociation constant are used.

Composition of an equilibrium mixture

When the only equilibrium is the formation of 1:1 adducts as the composition of a mixture, there are several ways that the composition of the mixture can be calculated. For example, see ICE table for a traditional method of calculating the pH of a weak acid solution. There are three methods for the general calculation of the composition of a mixture at equilibrium.

The most basic approach is to manipulate the different balance constants until the desired concentrations are expressed in terms of the measured balance constants (equivalent to the measurement of chemical potentials) and initial conditions.
Minimize Gibbs' energy from the system.
Satisfy the equation of mass balance. Mass balance equations are simply equations that show that the total concentration of each reactive must be constant according to the law of mass conservation.

Solving the mass balance equations

In general, the calculations are quite complicated. For example, in the case of a dibasic acid, H₂A dissolved in water the two reactants can be specified as the conjugate base, A^2-, and as the proton, H⁺. The following mass balance equations could equally be applied to a base such as 1,2-diaminoethane, in which case the base itself is designated reagent A.

{displaystyle T_{A}=[A]+[HA]+[H_{2}A],}

{displaystyle T_{H}=[H]+[HA]+2[H_{2}A]-[OH],}

With T_A like the total concentration of A species. Note that it is customary to omit the ionic loads when writing and using these equations. When the balance constants are known and the total concentrations are specified there are two equations with unknowns, the "free concentrations" ${displaystyle [A]}$ and ${displaystyle [H]}$ . This is deduced from the fact that ${displaystyle [HA]=beta _{1}[A][H]}$ , ${displaystyle [H_{2}A]=beta _{2}[A][B]^{2}}$ and ${displaystyle [OH]=K_{w}[H]^{-1}}$ .

{displaystyle T_{A}=[A]+beta _{1}[A][H]+beta _{2}[A][H]^{2},}

{displaystyle T_{H}=[H]+beta _{1}[A][H]+2beta _{2}[A][H]^{2}-K_{w}[H]^{-1},}

thus the concentrations of the "complexes" they are calculated from the free concentrations and the equilibrium constants. General expressions applicable to all systems with two reactants, A and B could be

{displaystyle T_{A}=[A]+sum _{i}{p_{i}beta _{i}[A]^{p_{i}}[B]^{q_{i}}}}

{displaystyle T_{B}=[B]+sum _{i}{q_{i}beta _{i}[A]^{p_{i}}[B]^{q_{i}}}}

It's easy to see how this can be extended to three or more items.

Composition of polybasic acids as a function of pH

The composition of solutions containing reagents A and H is easy to calculate as a function of pH. When [H] is known, the free concentration [A] is calculated from the mass balance equation in A. Here is an example of the results that can be obtained.

Hydrolysis of aluminum hydroxide.

This diagram, for the hydrolysis of Lewis acid aluminum Al³⁺_(aq) shows the concentrations of the species for a 5×10^-6M of an aluminum salt as a function of pH. Each concentration is shown as a percentage of total aluminum.

Equilibria in solution with precipitation

The diagram above illustrates the point at which a precipitate that is not one of the major species in equilibrium in solution forms. At pH below 5.5 the main species present in a 5 μM Al³⁺ solution are aluminum hydroxides, Al(OH)²⁺, Al(OH)₂⁺ and Al₁₃(OH)₃₂⁷⁺, but at raising the pH precipitates Al(OH)3 from solution. This is because Al(OH)₃ has a very large lattice energy. As the pH gets higher and higher, the Al(OH)₃ comes out of solution. This is an example of Le Châtelier's principle in action: An increase in the hydroxide ion concentration [OH^-) causes more aluminum hydroxide to precipitate, removing hydroxide from solution. When the hydroxide concentration becomes high enough, soluble aluminate, Al(OH)₄^-, is formed. Another common example is where precipitation occurs when a metal cation interacts with an anionic ligand to form an electrically neutral complex. If the complex is hydrophobic, it precipitates out of the water. This occurs with the nickel ion Ni²⁺ and dimethylglyoxime, (dmgH2): in this case the lattice energy of the solid is not particularly large, but it greatly exceeds the solvation energy of the Ni(dmgH)₂.

Minimization of the Gibbs energy

In balance, $G$ is a minimum:

{displaystyle mathrm {d} G=sum _{j=1}^{m}mu _{j},mathrm {d} N_{j}=0}

for a closed system, with no particles to enter or leave, even though they can combine in various ways. The total number of atoms of each element will remain constant. This means that the previous minimization is subject to restrictions:

{displaystyle sum _{j=1}^{m}a_{ij}N_{j}=b_{i}^{circ }}

where $a_{ij}$ is the number of atoms of the element i in the molecule j and b_i^or is the total number of atoms of the element iwhich is constant, since the system is closed. If there is a total of k types of atoms in the system, then there will be k equations of these. This is a standard optimization problem, known as restricted minimization. The most common method of solving it is through the method of Lagrange multipliers, also known as undetermined multipliers (although other methods can also be used). Define:

{displaystyle {mathcal {G}}=G+sum _{i=1}^{k}lambda _{i}left(sum _{j=1}^{m}a_{ij}N_{j}-b_{i}^{circ }right)=0}

where ${displaystyle lambda _{i}}$ are the Lagrange multipliers, one for each element. This allows each of the ${displaystyle N_{j}}$ be treated independently, and can be demonstrated by the tools of multivariate calculation that the condition of balance is given by:

{displaystyle {frac {partial {mathcal {G}}}{partial N_{j}}}=0}

and

{displaystyle {frac {partial {mathcal {G}}}{partial lambda _{i}}}=0}

(To deepen see Lagrange multipliers.) This is a set of (m + k) equations with "(m + k) unknowns ( ${displaystyle N_{j}}$ and the ${displaystyle lambda _{i}}$ ) and can therefore be resolved for balance concentrations ${displaystyle N_{j}}$ as long as chemical potentials are known as the functions of concentrations at the given temperature and pressure. (See thermodynamic databases for pure substances).This method of calculating chemical balance concentrations is useful for systems with a large number of different molecules. Use of kconservation equations of the atomic element for the restriction of the mass is simple, and replaces the use of stokyometric coefficient equations.

Spontaneity

To determine if a process is spontaneous or not, we must take into account the variation of enthalpy and entropy, since sometimes they contradict each other. On the one hand, enthalpy tells us that a process tends towards spontaneity, while entropy shows the opposite. Thus, it is necessary to evaluate both to establish whether or not a process is definitely spontaneous under certain conditions.

Gibbs' energy, $G$ , is the energy released by a system to perform useful work at constant pressure. Consider both changes in such a way that:

${displaystyle Delta G=Delta H-TDelta S}$

Gibbs' energy variation ${displaystyle Delta G}$ , it is a state function and has power units. So, if a chemical reaction releases useful work no matter what happens in the universe, ${displaystyle Delta G}$ is negative and therefore will be a spontaneous reaction, since it considers the dispersion of energy $<math alttext="{displaystyle Delta HΔ Δ H.0{displaystyle Delta H vis0} <img alt="{displaystyle Delta H$ and the dispersion of matter $0}" xmlns="http://www.w3.org/1998/Math/MathML">Δ Δ S▪0{displaystyle Delta S/20050}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/1f06ae07045a5a27238316606c89a2e3967798ce" style="vertical-align: -0.338ex; width:7.696ex; height:2.176ex;"/>$ in the system.

In this way, if a reaction occurs at low temperatures with a small change of entropy, then the term ${displaystyle T,mathrm {d} S}$ will be insignificant and ${displaystyle mathrm {d} G}$ will depend mainly on ${displaystyle mathrm {d} H}$ .

Endothermal reactions occur only if ${displaystyle T,mathrm {d} S}$ It's big. The temperature has to be high or there has to be a large increase in entropy to predominate this term and to determine the value of the ${displaystyle Delta G}$ .

Yes:

$<math alttext="{displaystyle Delta GΔ Δ G.0{displaystyle Delta G vis0} <img alt="{displaystyle Delta G$ The reaction is spontaneous in the sense established.

$0}" xmlns="http://www.w3.org/1998/Math/MathML">Δ Δ G▪0{displaystyle Delta G/20050}0}" aria-hidden="true" class="mwe-math-fallback-image-inline" src="https://wikimedia.org/api/rest_v1/media/math/render/svg/02ec7c4dd1b9e9df83dbcef5f800f3ec84ac3ed4" style="vertical-align: -0.338ex; width:8.024ex; height:2.176ex;"/>$ The reaction is not spontaneous in the sense established.

${displaystyle Delta G=0}$ The system is in balance.

Gibbs' energy standard reaction, ${displaystyle Delta _{mathrm {r} }G^{circ }}$ is the change of standard product energy less the change of standard reagent energy

${displaystyle Delta _{mathrm {r} }G^{circ }=sum _{j}n_{j}Delta G_{j}^{circ }-sum _{i}n_{i}Delta G_{i}^{circ }}$

Where:

${displaystyle n_{j}}$ is the schiometric coefficient of the products.
${displaystyle Delta G_{j}^{circ }}$ is the standard Gibbs energy variation of products.
${displaystyle n_{i}}$ is the schiometric coefficient of the reagents.
${displaystyle Delta G_{i}^{circ }}$ is the standard Gibbs energy variation.

It is considered for the elements in their most stable form in standard conditions ${displaystyle Delta G^{circ }=0}$ .

To read more

F. Van Zeggeren and S.H. Storei

Contenido relacionado

Más resultados...