Cartesian coordinates

ImprimirCitar

Three examples of coordinates assigned to three different points (green, red and blue), their orthogonal projections on the axis constitute their Cartesian coordinates and the origin of coordinates (0.0) in magenta.

The Cartesian coordinates or rectangular coordinates (Cartesian system) are a type of orthogonal coordinates used in Euclidean spaces, for the graphical representation of a mathematical relationship, movement or position in physics, characterized by having mutually orthogonal axes as references that meet at the point of origin. In Cartesian coordinates, the coordinates to the origin are determined as the length of each of the orthogonal projections of a given point on each of the axes. The denomination of 'Cartesian' It was introduced in honor of René Descartes, who first used it in a formal way.

Cartesian coordinates are used, for example, to define a Cartesian system or reference system with respect to either a single axis (straight line), with respect to two axes (a plane, thus being a system two-dimensional) or with respect to three axes (in space), perpendicular to each other (plane and space), which intersect at a point called origin of coordinates. In the plane, Cartesian coordinates are called abscissa and ordinate. The abscissa is the horizontal coordinate and is usually represented by the letter x, while the ordinate is the vertical coordinate and is represented by the letter y.

When the two lines intersect, they divide the plane into four regions or zones, which are known as quadrants:

First quadrant "I": Upper right area
Second quadrant "II": Upper left
Third quadrant "III": Lower left
Quadrant room "IV": Lower right

The Cartesian plane is used to assign a location to any point on the plane. The graph indicates the point +2 on the abscissa and +3 on the ordinate. The set (2 3) is called an "ordered pair" and in the same way other points can be located. The quadrant has 4 negative and positive points since the left side is called negative which is -x, -y and the right side is positive +x,+y.

History

Graphic of a hipperbola and her asymptoons.

They are called Cartesian coordinates after René Descartes (1596-1650), the famous French philosopher and mathematician who wanted to base his philosophical thought on the method of taking an obvious "starting point" on the one who would build all knowledge.

As the creator of analytic geometry, Descartes also began by taking a "starting point" in this discipline, the Cartesian reference system, in order to represent plane geometry, which uses only two intersecting perpendicular lines. point called the "origin of coordinates".

Cartesian plane

With a reference system made up of two perpendicular lines that intersect at the origin, each point of the plane can be "named" by means of two numbers: (x, y), which are the coordinates of the point, called abscissa and ordinate, respectively, which are the orthogonal distances of said point with respect to the axes Cartesians.

La equation axis $x$ That's it. ${displaystyle y=0}$ and the axis $y$ That's it. ${displaystyle x=0}$ , straights cut in the origin $O$ whose coordinates are ${displaystyle (0,0)}$ .

It is also called axis of abscises axis $x$ and axis of orders axis $y$ . The axles divide the space into four squares I, II, III and IV, in which the signs of the coordinates alternate from positive to negative (for example, the two coordinates of point A will be positive, while those of point B will be both negative).

The coordinates of any point will be given by the projections of the segment between the origin and the point on each of the axes.

Over each of the axes, unit vectors (i and j) are defined as those parallel to the y axes of module (length) unit. In vector form, the position of point A is defined with respect to the origin with the components of the vector OA.

{displaystyle {overline {OA}}=x_{A},mathbf {i} +y_{A},mathbf {j} }

The position of point A will be:

{displaystyle A=(x_{A},,y_{A})}

Note that the list of coordinates can express both the position of a point and the components of a vector in matrix notation.

The distance between any two points will be given by the expression:

{displaystyle d_{overline {AB}}={sqrt {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}}},}

Application of the Pythagorean theorem to the right triangle ABC.

Any vector AB will be defined by subtracting, coordinate by coordinate, those of the point of origin from those of the destination point:

{displaystyle {overline {AB}}=(x_{B}-x_{A}),mathbf {i} +(y_{B}-y_{A}),mathbf {j} }

Obviously, the magnitude of the vector AB will be the distance d_AB between the points A and B previously calculated.

Euclidean space

If we have a reference system consisting of three perpendicular straights (X, Y, Z), which are cut at the origin (0, 0, 0), each point of space can to be appointed using three numbers: (x, y, z), called coordinates of the point, which are the orthogonal distances to the three main planes: those containing the pairs of axes YZ, XZ and YX, respectively.

The XY reference planes (z = 0); XZ(y=0); and YZ (x = 0) divide the space into eight quadrants in which, as in the previous case, the signs of the coordinates can be positive or negative.

The generalization of the previous relations to the spatial case is immediate considering that now a third coordinate (z) is necessary to define the position of the point.

{displaystyle {overline {OA}}=x_{A},mathbf {i} +y_{A},mathbf {j} +z_{A},mathbf {k} }

The coordinates of point A will be:

{displaystyle A=(x_{A},,y_{A},,z_{A})}

and the B:

{displaystyle B=(x_{B},,y_{B},,z_{B})}

The distance between points A and B will be:

{displaystyle d_{overline {AB}}={sqrt {(x_{B}-x_{A})^{2}+(y_{B}-y_{A})^{2}+(z_{B}-z_{A})^{2}}},}

The segment AB will be:

{displaystyle {overline {AB}}=(x_{B}-x_{A}),mathbf {i} +(y_{B}-y_{A}),mathbf {j} +(z_{B}-z_{A}),mathbf {k} }

Changing the coordinate system

Both in the planar case and in the spatial case, three elementary transformations can be considered: translation of the origin, rotation around an axis and scaling.

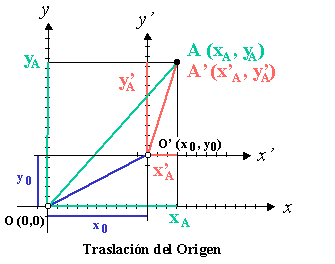
Translation of origin

Assuming an initial coordinate system S1 with origin at O and axes x and y

{displaystyle S1={O;;x,y}}

and the coordinates of a given point A, are in the system S1:

{displaystyle A=(x_{A},;y_{A})}

given a second frame of reference S2

{displaystyle S2={O^{prime };;x^{prime },y^{prime }}}

Being the coordinate centers of the systems 0 and 0´, different points, and the axes x, x´ ; e y, y´ parallel two by two, and the coordinates of O´, with respect to S1:

{displaystyle O^{prime }=(x_{O^{prime }},;y_{O^{prime }})}

We say translation of the origin, to calculate the coordinates of A in S2, according to the previous data, which we will call:

{displaystyle A^{prime }=(x_{A}^{prime },;y_{A}^{prime })}

Given the points O, O´ and A, we have the sum of vectors:

{displaystyle {overline {OA}}={overline {OO^{prime }}}+{overline {O^{prime }A}}}

clearing

{displaystyle {overline {O^{prime }A}}={overline {OA}}-{overline {OO^{prime }}}}

Which is the same as:

{displaystyle (x_{A}^{prime },;y_{A}^{prime })=(x_{A},;y_{A})-(x_{O^{prime }},;y_{O^{prime }})}

Separating the vectors by coordinates:

{displaystyle x_{A}^{prime }=x_{A}-x_{O^{prime }}}

{displaystyle y_{A}^{prime }=y_{A}-y_{O^{prime }}}

and expanding it to three dimensions:

{displaystyle z_{A}^{prime }=z_{A}-z_{O^{prime }}}

Rotation around the origin

Given a coordinate system in the plane S₁ with origin at O and axes x and and:

{displaystyle S_{1}={O;;x,y}}

and an orthonormal basis of this system:

{displaystyle B_{1}={mathbf {i}mathbf {j} }}

A point A on the plane will be represented in this system according to its coordinates:

{displaystyle mathbf {A} =x_{A},mathbf {i} +y_{A},mathbf {j} }

For a second system S₂ referenced angle ${displaystyle alpha ,}$ regarding the first:

{displaystyle S_{2}={O;;x^{prime },y^{prime }}}

and with an orthonormal basis:

{displaystyle mathbf {B} _{2}={mathbf {i^{prime }}mathbf {j^{prime }} }}

The calculation of the coordinates of point A, with respect to this second reference system, rotated with respect to the first, is called rotation around the origin, its representation being:

{displaystyle {mathbf {A} ^{prime }}=x_{A}^{prime },mathbf {i^{prime }} +y_{A}^{prime },mathbf {j^{prime }} }

You have to keep in mind that the point ${displaystyle mathbf {A} ,}$ and ${displaystyle mathbf {A} ^{prime },}$ It's the same point, ${displaystyle mathbf {A} equiv mathbf {A} ^{prime }}$ ; one name or another is used to indicate the reference system used. The value of the coordinates regarding one or another system, are different, and that is what is intended to be calculated.

The representation of B₁ in B₂ is:

{displaystyle mathbf {i} =cos {alpha },mathbf {i^{prime }} -sin {alpha },mathbf {j^{prime }} }

{displaystyle mathbf {j} =sin {alpha },mathbf {i^{prime }} +cos {alpha },mathbf {j^{prime }} }

Given that point A in B1 is:

{displaystyle mathbf {A} =x_{A},mathbf {i} +y_{A},mathbf {j} }

with the previous transformation we have:

{displaystyle mathbf {A} =x_{A},(cos {alpha },mathbf {i^{prime }} -sin {alpha },mathbf {j^{prime }})+y_{A},(sin {alpha },mathbf {i^{prime }} +cos {alpha },mathbf {j^{prime }})}

And, undoing the parentheses:

{displaystyle mathbf {A} =x_{A},cos {alpha },mathbf {i^{prime }} -x_{A},sin {alpha },mathbf {j^{prime }} +y_{A},sin {alpha },mathbf {i^{prime }} +y_{A},cos {alpha },mathbf {j^{prime }} }

reordering:

{displaystyle mathbf {A} =(x_{A},cos {alpha }+y_{A},sin {alpha }),mathbf {i^{prime }} +(-x_{A},sin {alpha }+y_{A},cos {alpha }),mathbf {j^{prime }} }

Like:

{displaystyle mathbf {A} equiv A^{prime }}

;

We have to:

{displaystyle mathbf {A^{prime }} =(x_{A},cos {alpha }+y_{A},sin {alpha }),mathbf {i^{prime }} +(-x_{A},sin {alpha }+y_{A},cos {alpha }),mathbf {j^{prime }} }

As we knew:

{displaystyle mathbf {A^{prime }} =x_{A}^{prime },mathbf {i^{prime }} +y_{A}^{prime },mathbf {j^{prime }} }

By identifying terms:

{displaystyle x_{A}^{prime }=;x_{A},cos {alpha }+y_{A},sin {alpha }}

{displaystyle y_{A}^{prime }=-x_{A},sin {alpha }+y_{A},cos {alpha }}

What are the coordinates of A in B₂, depending on the coordinates A in B₁ and ${displaystyle {alpha },}$ .

Scaling

Let be a point with coordinates (x,y) in the plane. If both axes are scaled by a λ factor, the coordinates of that point in the new coordinate system will become:

{displaystyle (x',y')=(lambda x,lambda y),}

The scale factor λ does not necessarily have to be the same for both axes.

Matrix calculation

Being [T] the transformation matrix and whose rows are also the components of the unit vectors i ' and j ' with respect to the originals i and j, or if preferred, whose columns are the components of the original unit vectors in the rotated frame of reference.

Note: Vector quantities are in bold.

Additional bibliography

Brannan, David A.; Esplen, Matthew F.; Gray, Jeremy J. (1998), Geometry (in English), Cambridge: Cambridge University Press, ISBN 978-0-521-59787-6.
Burton, David M. (2011), The History of Mathematics/An Introduction (in English) (7th edition), New York: McGraw-Hill, ISBN 978-0-07-338315-6.
Smart, James R. (1998), Modern Geometries (in English) (5th edition), Pacific Grove: Brooks/Cole, ISBN 978-0-534-35188-5.
Descartes, René (1637), Le Livre Premier de La Géométrie de Descartes (in French), "livre premiere".
Descartes, René; Paul J. Oscamp (Translator) (2001). Discourse on Method, Optics, Geometry, and Meteorology (in English) (Revised edition). Indianapolis, IN: Hackett Publishing. ISBN 978-0-87220-567-3. OCLC 488633510.
Korn GA, Korn TM (1961). Mathematical Handbook for Scientists and Engineers (in English) (1st edition). New York: McGraw-Hill. pp. 55–79}. LCCN 59014456. OCLC 19959906. (requires registration).
Margenau H, Murphy GM (1956). The Mathematics of Physics and Chemistry (in English). New York: D. van Nostrand. LCCN 55010911. (requires registration).
Moon P, Spencer DE (1988). "Rectangular Coordinates (x, y, z)". Field Theory Handbook, Including Coordinate Systems, Differential Equations, and Their Solutions (in English) (corrected 2nd, 3rd print edition). New York: Springer-Verlag. pp. 9-11 (Table 1.01). ISBN 978-0-387-18430-2.
Morse PM, Feshbach H (1953). Methods of Theoretical Physics, Part I (in English). New York: McGraw-Hill. ISBN 978-0-07-043316-8. LCCN 52011515.
Sauer R, Szabó I (1967). Mathematische Hilfsmittel des Ingenieurs (in German). New York: Springer Verlag. LCCN 67025285.

Contenido relacionado

Más resultados...