Bravais nets
In geometry and crystallography Bravais lattices are an infinite arrangement of discrete points whose structure is invariant under a certain group of translations. In most cases there is also invariance under rotations or rotational symmetry. These properties mean that all the nodes in a Bravais network have the same perspective of the network. The points of a Bravais lattice are then said to be equivalent.
By means of group theory it has been shown that there is only a single one-dimensional Bravais network, 5 two-dimensional networks and 14 different models of three-dimensional networks.
The one-dimensional network is elementary, being a simple sequence of nodes equidistant from each other. In two or three dimensions things get more complicated and the variability of shapes makes it necessary to define certain pattern structures to work comfortably with networks.
To generate these we normally use the concept of primitive cell. Unit cells are parallelograms (2D) or parallelepipeds (3D) that constitute the smallest subdivision of a crystal lattice that preserves the general characteristics of the entire lattice, so that by simply translating it, the entire lattice can be reconstructed in any point.
A typical network R in Rn{displaystyle mathbb {R} ^{n} has the form:
- R={␡ ␡ i=1n.. ia→ → i日本語.. i한 한 Z!{displaystyle R=left{sum _{i=1}{n}nu _{i}{i}{a}{i}_{i}{i}{i};
where {a1,..., an} is a basis in Rn space. There may be different bases that generate the same network, but the absolute value of the determinant of the vectors ai will always be determined by the network, so it can be represented as d(R).
Unit cells can be defined very simply from two vectors (2D) or three vectors (3D). The construction of the cell is done by drawing the parallels of these vectors from their ends to the point where they intersect. There is a type of unit cell that is built in a different way and that presents certain advantages in the visualization of the network since it has the same symmetry as the network, it is the Wigner-Seitz cell. A unit cell is characterized mainly by containing a single network node, hence the adjective "unitary". Although in many cases there are different shapes for the unit cells of a given lattice, the volume of every unit cell is always the same.
Features
Sometimes it is easier to build other types of cells that, without being unitary, better describe the structure of the network we are dealing with. These types of cells are called conventional cells. These, in turn, have their own network parameters and a certain volume.
All these cells are considered primitive cells since they are capable of covering the entire space through translations without leaving any gaps or overlaps. Their differences or characteristics are the following:
Close packing: This is when the atoms in the cell are in contact with each other. This will not always be the case and in many cases there will be a minimum distance between the electronic clouds of the different atoms.
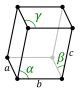
Lattice parameter: It is the length of the sides of the unit cell. There can be as few as one, two or even three different lattice parameters depending on the type of Bravais lattice we are dealing with. In the most common structures it is represented by the letter a and by c if there are two.
Nodes or atoms per cell: As the name says, it is the number of nodes or atoms that each cell has. A square cell, for example, will have one node per cell since each corner shares it with four other cells. In fact, if a cell has more than one network node, it is not unitary. On the other hand, if it has more than one atom per cell, it could be that we are in a unit cell but with an atomic base of more than one atom.
Coordination number: It is the number of closest network points, the first neighbors, of a network node. If it is a structure with close packing, the coordination number will be the number of atoms in contact with another. The maximum is 12.
Atomic Packing Factor: Fraction of unit cell space occupied by atoms, assuming they are solid spheres.
f=n⋅ ⋅ vVc{displaystyle f={frac {ncdot v}{V_{c}}}}
Where f is the packing factor or volume fraction, n the number of atoms per cell, v the volume of the atom and Vc the volume of the cell. Normally, the close packing factor for the different cells is given as an indicator of the density of atoms that each crystalline structure has. In this case the atoms are treated as rigid spheres in contact with their nearest neighbors.
Density: From the characteristics of the network, the theoretical density of the material that makes up the network can be obtained using the following expression.
ρ ρ =n⋅ ⋅ mNA⋅ ⋅ Vc{displaystyle rho ={frac {ncdot m}{N_{A}cdot V_{c}}}}}}
Where ρ is the density, NA the Avogadro number and m the atomic mass.
Volume of the primitive unitary cell: Every unit cell has the same volume represented by the following formula. vcup=日本語a→ → 1(a→ → 2× × a→ → 3)日本語{displaystyle v_{cup}= meant{vec {a}_{1}({vec {a}}}}_{2times {vec {a}}}{3}})Where a are the vectors of the network base.
Two-dimensional networks
According to the angles and the distance between the nodes, 5 different networks can be distinguished.
Three-dimensional networks
Depending on the parameters of the unit cell, the lengths of its sides and the angles they form, 7 crystalline systems can be distinguished.
To fully determine the elemental crystalline structure of a solid, in addition to defining the geometric shape of the lattice, it is necessary to establish the positions in the cell of the atoms or molecules that make up the crystalline solid; what are called lattice points. The alternatives are the following:
- Q: Primitive or simple cell in which the reticular points are only the vertices of the parallelepipe.
- F: Cell focused on the faces, which has reticular points on the faces, in addition to the vertices. If they only have reticular points in the bases, they are designated with letters A, B or C as the faces that have the two reticular points.
- B: Cell centered on the body, which has a reticular point in the center of the cell, in addition to the vertices.
- C: Primitive with equal axes and equal or hexagonal angles double-centered in the body, plus vertices.
Combining the 7 crystalline systems with the arrangements of the mentioned lattice points, 28 possible crystalline lattices would be obtained. In reality, as can be shown, there are only 14 basic configurations, and the rest can be derived from them. These structures are called Bravais networks.
| Crystal system | Bravais Networks | |||
| trillion | P | |||
 | ||||
| monoclinic | P | C | ||
 |  | |||
| orthrombic | P | C | B | F |
 |  | 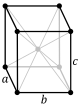 |  | |
| tetragonal | P | B | ||
 |  | |||
| Romboédrico (trigonal) | P | |||
 | ||||
| hexagonal | P | |||
 | ||||
| cubic | P | B | F | |
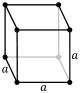 |  |  | ||
Atomic basis
In the simplest case, each lattice point will correspond to one atom, but in more complicated structures, such as ceramics and composites, hundreds of atoms can be associated with each lattice point, forming extremely complex unit cells. The distribution of these additional atoms or molecules is called the atomic basis and this gives us their distribution within the unit cell.
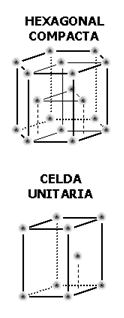
There are two typical cases of atomic bases. The diamond structure and the compact hexagonal. For two-dimensional networks, an exemplary case would be graphite whose structure follows a honeycomb network pattern.
| Structure | a (r) | Number of coordination | Number of atoms by cell | Factor packaging | Examples | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Simple cubicle (CS) | a = 2r | 6 | 1 | 0.52 | Po | ||||||||
| Body-centered cubicle (BCC) | a = 4r/Ã3 | 8 | 2 | 0.68 | Fe, W, Mo, Nb, Ta, K, Na, V, Cr, Zr | ||||||||
| Face-centered cubicle (FCC) | a = 4r/Ã2 | 12 | 4 | 0.74 | Cu, Al, Au, Ag, Pb, Ni, Pt | ||||||||
| Hexagonal Simple (HS) | a = 2r | 8 | 3 | 0.60 | Pm, Tl, Tc, Gd, Tb, Lu | ||||||||
| Compact Hexagonal (HCP) | a = 2r | Parameter for the coordination number = c/ a c = Hexagonal cell height A Side of the hexagonal cell
| 6 | 0.74 | Ti, Mg, Zn, Be, Co, Zr, Cd | ||||||||
The names (BCC, HCP, FCC) are in international or English nomenclature.
Contenido relacionado
Carl Friedrich Gauss
Archimedes
Levi-Civita symbol