Bisector

The perpendicular bisector of a segment is the straight line perpendicular to said segment drawn by its midpoint. Equivalently, it can be defined as the locus — the line — whose points are equidistant from the endpoints of the segment.

Description

The straight r is the mediatrix of the segment AB. Any point (P) of it, equidistant of the end of the segment A and B (AP = BP).

Indeed, ${displaystyle} AB$ any segment, determined by the points ${displaystyle A}$ and ${displaystyle B}$. Sea ${displaystyle M}$ the midpoint of the segment and ${displaystyle r}$ the line perpendicular to the segment by that point. Sea ${displaystyle P}$ a point on the straight ${displaystyle r}$. In axial symmetry regarding the straight ${displaystyle r}$The point ${displaystyle P}$ is invariant and the points ${displaystyle A}$ and ${displaystyle B}$ They are the symmetrical of the other. Therefore, in this symmetry, the segment ${displaystyle AP}$ transforms into the segment ${displaystyle BP}$, both segments are congruent and the point ${displaystyle P}$ equidistant points ${displaystyle A}$ and ${displaystyle B}$. Consequently, every point that is found on the straight ${displaystyle r}$ belongs to the mediatrix of the segment in question.

reciprocally. ${displaystyle} AB$ a segment and ${displaystyle P}$ a point that equidistates ${displaystyle A}$ and ${displaystyle B}$, this is the segments ${displaystyle AP}$ and ${displaystyle BP}$ They're the same. Consider the bisectr ${displaystyle R}$ angle ${displaystyle APB}$ and be ${displaystyle M}$ the intersection of such bisectriz with the segment ${displaystyle} AB$.

By construction, the angles ${displaystyle APM}$ and ${displaystyle BPM}$ are equal and in axial symmetry with respect to the straight ${displaystyle r}$ they become one another. Like segments ${displaystyle PA}$ and ${displaystyle PB}$ are equal, in this symmetry, the points ${displaystyle A}$ and ${displaystyle B}$ they are one another's image. We concluded that the point ${displaystyle M}$ is midpoint of the segment ${displaystyle} AB$ and that such segment is perpendicular to the straight ${displaystyle r}$.

Graphic construction of the perpendicular bisector

To draw the perpendicular bisector of a given segment AB, draw two arcs of arbitrary equal radius (always greater than half the length of the segment) with centers at the endpoints of the segment. The two arcs will intersect at two points C and D that belong to the perpendicular bisector, since they meet the condition of equidistar from the ends of the segment.

Graphical construction of the mediator with rule and compass.

Applications in geometry

La average of a rope passes through the center of the circumference.

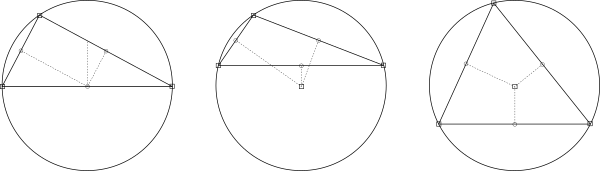
The bisectors of a cyclic polygon are the bisectors of its sides, that is, the perpendiculars to the sides that pass through their midpoints. These intersect at a point called the circumcenter, which is the center of the circle that passes through the vertices of the polygon, that is, of the circumcircle of the polygon.

This is because the perpendicular bisector of a given chord in any circumference necessarily passes through its center. Applying the perpendicular bisectors to the sides of the cyclic polygon as if they were chords of the circumference, we obtain that their intersections constitute the center of the circle that contains all of them and therefore, the circumscribed circle.

Not all simple convex polygons are cyclic polygons, cyclic polygons include all triangles, cyclic quadrilaterals, and all simple regular polygons.

Circumcenter

Due to the aforementioned property, in every triangle ABC the perpendicular bisectors of its three sides meet at the same point, called the circumcenter (O) of the triangle. Said point is equidistant from the vertices of the triangle. The circle with center O and radius OA passes through the other two vertices of the triangle. It is said that said circle is circumscribed to the triangle and that the triangle is inscribed in the circle.

From left to right, the circumcenter of a rectangle triangle, obtussangle and acumultangle.