Binary tree
In computer science, a binary tree is a data structure in which each node can have one left child and one right child. They cannot have more than two children (hence the name 'binary'). If any child references null, that is, it does not store any data, then it is called an external node. Otherwise the child is called an internal node. Common uses of binary trees are binary search trees, binary heaps, and Huffman coding.
Definition of graph theory
In graph theory, the following definition is used: "A binary tree is an undirected, acyclic, connected graph such that the degree of each vertex is no greater than 2." Thus, there is only one path between a pair of nodes.
A rooted binary tree is like a graph that has one of its vertices, called root, of degree no greater than 2. With the root chosen, each vertex will have a unique parent, and never more than two children. If we waive the connectivity requirement, allowing multiple connected components in the graph, we will call this last structure a forest'.
Types of binary trees
A binary tree is a tree in which no node can have more than two subtrees. In a binary tree, each node can have zero, one, or two children (subtrees). The node on the left is known as the left child and the node on the right is known as the right child.
There are types of binary trees that are often used for specific purposes, such as:
- binary search tree
- Fibonacci tree
C implementation
A binary tree can be declared in several ways. Some of them are:
Structure with dynamic memory management, being the pointer that points to the tree of type tTree:
typedef struct No. { int key; struct No. ♪izdo, ♪dcho;!No.;Structure with indexed array:
typedef struct tArbol
{
int key;
Left tree, right;
Tree.
tA tree[NEW];
In the case of an almost-complete binary tree (or a complete tree), a simple array of integers can be used with as many positions as there are nodes in the tree. Information about the location of the node in the tree is implicit at each position in the array. Thus, if a node is at position i, its children are at positions 2i+1 and 2i+2, while that its parent (if any), is at position truncation((i-1)/2) (assuming the root is at position zero). This method benefits from more compact storage and better reference locality, particularly during a preorder run. The structure for this case would therefore be:
int tree[NUMERO_DE_NODOS];
Traversals over binary trees
In-Depth Tours
The method of this traversal is to try to find from head to root in binary unit node. Now we will see the implementation of the different routes:
Preorder Tour
In this type of traversal, some action (perhaps simply printing the value of that node's key to the screen) is performed on the current node, and then the left subtree is processed, and when complete, the right subtree. Another way to understand the traversal with this method would be to follow the order: root node, left node, right node.
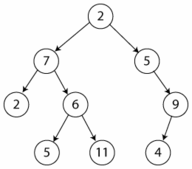
In the tree of the figure, the path in preorder would be: 2, 7, 2, 6, 5, 11, 5, 9 and 4.
void preorden(tArbol *a)
{
if (a != NULL) {
treat(a); //Realizes a node operation
preorder(a-purchase left);
preorder(a-g.
!
!
Pseudocode implementation iteratively:
push(s,NULL); //install on a stack (stack) the NULL value, to make sure it is empty push(s, root); //insert root node MIENTRAS (s Δ NULL) HACER p = pop(s); //let's get a battery element treat(p); //we perform operations on the p node SI (D(p) ≤ NULL) // ask if p has a right tree ENTONCES push(s,D(p)); FIN-SI SI (I(p) ≤ NULL) // ask if p has left tree ENTONCES push(s, I(p)); FIN-SI FIN-MIENTRAS
Postorder traversal
In this case, the left subtree is treated first, then the right, and lastly the current node. Another way to understand the traversal with this method would be to follow the order: left node, right node, root node. In the tree in the figure, the postorder path would be: 2, 5, 11, 6, 7, 4, 9, 5 and 2.
void postorden(tArbol *a)
{
if (a != NULL) {
postorden(a-105hIzquiedo);
postorden(a-105hRight);
treat(a); //Realizes a node operation
!
!
Travel in disorder
In this case, the left subtree is treated first, then the current node, and finally the right subtree. On an ABB this walkthrough would give the key values ordered from lowest to highest. Another way to understand the traversal with this method would be to follow the order: left node, root node, right node. In the tree of the figure, the path in inorder would be: 2, 7, 5, 6, 11, 2, 5, 4, 9.
Implementation scheme:
void inorden(tArbol *a)
{
if (a != NULL) {
inorden(a-105h Left);
treat(a); //Realizes a node operation
inorden(a-105hRight);
!
!
Traversals in breadth (or by levels)
In this case, the route is carried out in order through the different levels of the tree. Thus, one would begin by treating level 1, which only contains the root node, then level 2, 3, and so on. In the tree of the figure, the path in amplitude would be: 2, 7, 5, 2, 6, 9, 5, 11 and 4.
Unlike depth traversal methods, level traversal is not recursive in nature. Therefore, a queue must be used to remember the left and right subtrees of each node.
The algorithm scheme to implement a level traversal is exactly the same as the one used in the iterative version of the preorder traversal but changing the data structure that stores the nodes by a queue.
C implementation:
void arbol_recorrido_anch (type_ Tree♪ A) { type_Cola queue_nodos; // This queue is previously implemented, stores pointers (positions of tree nodes) type_Pos node_actual; // this is a pointer to take the tour if (Empty(A) // if the tree is empty, we go out return; tail_start("queue_nodos); // obvious, and necessary queue(A, "queue_nodos); // the root shrinks while (!emptied("queue_nodos) { // as long as the queue does not empty, the tour will take place node_actual = queue("queue_nodos) // of the tail will go out the nodes sorted by level printf("%c,", node_actual- 2005info); // is "processed" the node where the route goes, in this case it is printed if (node_actual- 2005izq = null) // if it exists, we put the left son in the tail queue(node_actual- 2005izq, "queue_nodos); if (node_actual- 2005der = null) // if it exists, we put the right child in the tail queue(node_actual- 2005der, "queue_nodos); ! // By emptying the tail all the nodes of the tree have been visited !Creating trees from traversals
In order to draw a binary tree based on the traversals, at least two of the depth traversals are needed (in case the nodes are not repeated, since if the nodes are repeated it is advisable to have all three traversals), whether inorder and preorder or inorder and postorder, the only difference between using traversal in preorder or postorder is that in preorder the first node is used to find the root and in postorder the last node is used.
The method consists of dividing the tree traversals into small subtrees, the root is found with the preorder or postorder and it is divided into two subtrees based on the inorder traversal. In the event that the nodes are repeated, it is convenient to have the 3 traversals to more easily identify which of the nodes is the current root.
The following paths correspond to the tree in the figure:
Preorden 2,7,2,6,5,11,5,9,4{displaystyle 2,7,2,6,5,11,5,9.4}
Inorden 2,7,5,6,11,2,5,4,9{displaystyle 2,7,5,6,11,2,5,4,9}
Postorden 2,5,11,6,7,4,9,5,2{displaystyle 2,5,11,6,7,4,9,5,2}
To find the root it is necessary to have the route preorder or postorder, since the root is the first node or the last node respectively. In this case the root is 2{displaystyle 2}.
Once the root is found, it is necessary to know its position on the inorden route, the previous step has the node 2{displaystyle 2}but there are 2 nodes with that value, the first and the middle. If the first two is the root, then there is no branch on the left side, in that case the following root according to the postorder route is 5{displaystyle 5} and according to preorder is 7{displaystyle 7}, which is incongruity, so we know that the other 2{displaystyle 2} It's the root.
Then we mark the root in the inorder traversal:
Preorden 2_ _ ,7,2,6,5,11,5,9,4{displaystyle {underline {2}},7,2,6,5,11,5,4}
Inorden 2,7,5,6,11,2_ _ ,5,4,9{displaystyle 2,7,5,6,11,{underline {2}},5,4,9}
Postorden 2,5,11,6,7,4,9,5,2_ _ {displaystyle 2.5,11,6,7,4,9,5,{underline {2}}}}
The inorder traversal is a traversal of the binary trees in which it starts from the node that is furthest to the left of all, continues with the root and ends with the nodes on the right side, then, as in the inorder traversal we already found the root, the left part represents the left subtree and the right part represents the right subtree.
In the tours we have 5 nodes left of the 2{displaystyle 2} and to the right are 3 values, then we can create the paths for the left subtree and the right subtree
| Upstairs left | Right subtree |
|---|---|
| Preorden 7,2,6,5,11{displaystyle 7,2,6,5,11} | Preorden 5,9,4{displaystyle 5,9,4} |
| Inorden 2,7,5,6,11{displaystyle 2,7,5,6,11} | Inorden 5,4,9{displaystyle 5,4,9} |
| Postorden 2,5,11,6,7{displaystyle 2,5,11,6,7} | Postorden 4,9,5{displaystyle 4,9.5} |
It continues to repeat the process until you find all the nodes of the tree, at this point the next left root is the 7{displaystyle 7} and the right root 5{displaystyle 5}.
When they reach nodes in which they only have a branch it is necessary to know that branch is the right and which is the left (for some trees with swing like the AVL), for example following the branch of the right starting from that 5{displaystyle 5} is the root the inorden route is 5,4,9{displaystyle 5,4,9} then the next node goes to the right, there is no no node to the left, then the paths for the subtree are:
Preorden 9,4{displaystyle 9,4}
Inorden 4,9{displaystyle 4,9}
Postorden 4,9{displaystyle 4,9}
Finally the next node is placed to the left of the 9{displaystyle 9}.
This method is 100% effective when there are no repeat nodes, when the nodes repeat the complexity increases to discover which is the root node in the inorder traversal.
Methods for storing Binary Trees
Binary trees can be constructed from programming languages in various ways. In a language with records and references, binary trees are typically built with a structure of nodes and pointers in which data is stored, each of these nodes having a reference or pointer to a left node and a right node called children. Sometimes it also contains a pointer to a single node. If a node has fewer than two children, some of the child pointers may be defined as null to indicate that it does not have that node. The attached figure shows the structure of said implementation.
The binary trees can also be stored as an implicit data structure in vectors, and if the tree is a complete binary tree, this method does not waste the space in memory. We will take as a notation the following: if a node has an i index, your children are in 2i + 1 and 2i + 2, while your parents (if you have them) are in the index i− − 12 {displaystyle leftlfloor {frac {i-1}{2}}}rightrfloor } (from the root having zero index). This method has the advantages of having the data stored more compactly and having a faster and more efficient way of locating the data in particular during a cross-sectional preoden. However, it wastes a lot of space in memory.
Encoding n-ary trees as binary trees
There is a one-to-one mapping between general trees and binary trees, which in particular is used in Lisp to represent general trees as binary trees. Each node N ordered in the tree corresponds to a node N' in the binary tree; the left child of N' is the node corresponding to the first child of N, and the right child of N' is the node corresponding to the next sibling of N, that is, the next node in order among the children of the parents of N.
This binary tree representation of a general tree is sometimes known as a first child sibling binary tree, or a doubly chained tree.
One way to think about this is that the children of each node are in a linked list, chained together with the right field, and the node only has a pointer to the beginning or head of this list, via its left field.
For example, in the tree on the left, A has 6 children (B, C, D, E, F, G). It can be converted to the binary tree on the right:
The binary tree can be thought of as the original tree leaning to the sides, with the black left borders representing the first child and the blue ones representing the next siblings.
The leaves of the tree on the left would be written in Lisp as:
((N O) I J) C D ((P) (Q)) F (M))
Which will be executed in memory as the binary tree on the right, without any letters on those nodes that have a left child.
Contenido relacionado
AMD Athlon
IBM RS/6000
Gecko (software)